6.2.6 Упражнения

1. Пусть
$$f(x,y,z) = \frac {[\frac{x}{y}]! - \sin z}{[\frac{y}{x}]!+ \mid z \mid}.$$

Для заданных вещественных чисел $А$ и $В$ вычислить значение$f(A,(-2, 5B), (1, 13 + B^2)) + f(A+B,A,B).$

2. Дана последовательность целых чисел $n,$$a_1,$$\ldots,$$a_n,$$m,$$b_1,$$\ldots,$$b_m,$$k,$$c_1,$$\ldots,$$c_k$. Вычислить $d$ по формуле $d= \left \{ \begin{array}{l}\min(b_1,\ldots,b_m) + \max(c_1,\ldots,c_k),\\......_1,\ldots,b_m) - \min(c_1,\ldots,c_k), \mbox{ иначе } \\\end {array} \right.$

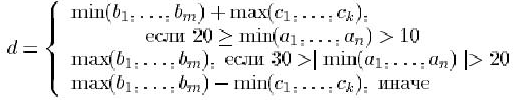
3. Даны вещественные числа $s,t,a_0,\ldots,a_{12}$. Вычислить $g(1) -g(t) + g^2(s-t) - g(10)$, где $g(x) = a_{12}x^{12} + a_{11}x^{11}+\ldots + a_0$ для любого вещественного $х$.

4. Три треугольника заданы координатами своих вершин. Определить

(1) пересекаются ли какие-нибудь два из треугольников,
(2) лежит ли какой-нибудь из треугольников целиком внутри первого,
(3) есть ли среди треугольников пара касающихся,
(4) есть ли у всех треугольников общая точка,
(5) есть ли среди треугольников два подобных,
(6) является ли больше заданной суммарная площадь двух из треугольников,
(7) есть ли среди треугольников прямоугольный.

5. Распечатать заданную последовательность нулей и единиц, изображая каждую цифру поперек листинга высотой в 50 см и отводя под ее изображение 25 см листа бумажной выдачи (т.е. 25 см -- ширина изображения цифры).

6. Задана последовательность из трех векторов, каждый из которых содержит 100 целых чисел. Найти

(1) номер вектора, в котором максимальна сумма четных элементов, расположенных на нечетных позициях,
(2) тот вектор, каждый элемент которого больше суммы соответствующих элементов двух других векторов,
(3) тот вектор, который перпендикулярен двум другим векторам (Два вектора $A=(a_1,\ldots,a_{100})$ и $B=(b_1,\ldots,b_{100})$ перпендикулярны, если $\sum_{i=1}^{100}a_ib_i=0$.),
(4) тот вектор, который не параллелен ни одному из двух других векторов (Два вектора $A=(a_1,\ldots,a_{100})$ и $B=(b_1,\ldots,b_{100})$ параллельны, если для некоторого вещественного$s$ справедливо утверждение $(\forall i: 1\leq i\leq 100: a_i-s\cdot b_i=0)$.),
(5) сумму номеров тех элементов векторов, которые являются полными квадратами и отличны от других элементов своего вектора,
(6) тот вектор, элементы которого расположены по возрастанию,
(7) тот вектор, в котором каждое число повторяется ровно пять раз.

7. Сведения об автомобиле состоят из его марки, номера и фамилии владельца. Даны три таблицы, в каждой из которых содержатся сведения о 100 автомобилях, размещенных в одном из гаражей. Определить тот гараж, в котором (по отношению к другим)

(1) меньше разных марок автомобилей,
(2) больше однофамильцев среди владельцев автомобилей,
(3) больше автомобилей таких марок как "Волга" и "Жигули",
(4) меньше максимальный номер автомобилей,
(5) меньше автомобилей, фамилии владельцев которых начинаются на буквы "Б", "Л" и "С".

8. Сведения об ученике состоят из его имени, фамилии, роста, веса, номера его школы и названия класса (года обучения и буквы), в котором он учится. Даны три таблицы, в каждой из которых содержатся сведения о 20 школьниках, составляющих баскетбольную команду города. Распечатать таблицу, содержащую информацию о команде, в которой

(1) средний рост школьников является наибольшим, а средний вес наименьшим среди средних весов команд, имеющих одинаковый средний рост,
(2) меньше учащихся из 10-Г класса 130 школы,
(3) больше учащихся восьмых классов из 130 и 25 школ, имена и фамилии которых начинаются с разных букв.

9. Даны три целочисленных матрицы размером 40 на 40. Напечатать ту из них, которая является

(1) суммой, т.е. $A(i,j)=B(i,j)+C(i,j)$ для всех $i$ и $j$,
(2) разностью, т.е. $A(i,j)=B(i,j)-C(i,j)$ для всех $i$ и $j$,
(3) произведением т.е. $A(i,j)=\Sigma_{k=1}^{40} B(i,k)\times C(k,j)$ для всех $i$ и $j$,
двух других матриц.

10. Даны четыре вещественных матрицы размером 50 на 50. Проверить, верно ли, что

(1) произведение первых двух из них (см. предыдущее упражнение) совпадает с произведением двух других матриц,
(2) матрица, являющаяся суммой первых двух матриц исходной последовательности, может быть получена транспонированием матрицы, являющейся суммой двух последних матриц исходной последовательности,
(3) для любых четырех элементов $a,b,c,d$, расположенных на одних и тех же местах исходных матриц, справедливо $a \leq b$ тогда и только тогда, когда $c \leq d$.

11. Дана последовательность A,B,C,D, состоящая из литерных матриц размером 100 на 100, вычислить матрицу $(A \oplus B)\oplus (C \oplus D)$, где $\oplus$ обозначает операцию преобразования любых двух литерных матриц $Х$ и $Y$ в такую литерную матрицу $Z$, что для любых $i$ и $j$

12. Задана последовательность из трех программ, текст каждой из которых не превышает 200 символов и не содержит комментариев. Допуская, что между соседними программами может находиться произвольное число пробелов, распечатать ту из этих программ, в которой

(1) наибольшее количество условных операторов,
(2) наименьшее количество операторов цикла и выбора,
(3) наибольшая глубина вложенности составных операторов,
(4) наибольшее количество целочисленных констант,
(5) наименьшее количество типов, определяемых для всей программы,
(6) наибольшее число переменных, область существования которых -- вся программа,
(7) наименьшее количество определений процедур и функций.

13. Проверить, верно ли, что совпадают количества столбцов, составленных только из отрицательных элементов, в трех вещественных матрицах размером 40 на 40, заданных по строкам.

14. Проверить, верно ли, что в последовательности литерных матриц размером 100 на 200 матрицы расположены в порядке убывания в них количества

(1) симметричных строк,
(2) несимметричных столбцов,
(3) строк, содержащих не более трех разных букв,
(4) строк, содержащих все четные цифры,
(5) столбцов, содержащих каждую букву и каждую цифру не менее двух раз.

15. Проверить, верно ли, что в заданной последовательности векторов $В_1,В_2,\ldots$, каждый из которых составлен из 200 натуральных чисел, для любого i$>$1 справедливо свойство $s_i >\max(r_i,g_i)$, где $s_i$ -- сумма тех нечетных элементов вектора $B_i$, которые являются точными квадратами, $r_i$ -- количество кратных 5 элементов вектора $B_{i-1}$, а $g_i$ -- это число 5, если $B_i$ -- последний элемент заданной последовательности, либо количество нечетных чисел, кратных 5 и расположенных на четных позициях вектора $B_{i+1}$.

16. Вычислить значение функции Аккермана

$A(n,m) = \left \{ \begin{array}{ll}m+1, & \mbox{ если } n = 0, \\A(n-1,1) ......, \\A(n-1, A(n,m-1)), & \mbox{ если } n > 0, m > 0 \\\end{array} \right.$

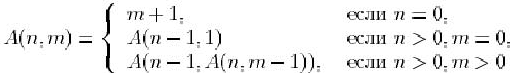
для заданных натуральных $n,m$. Докажите, что программа заканчивается при любых $n\geq 0, m\geq 0$ и вычисляет значение, большее $n+m$.

17. Вычислить число сочетаний $C_n^k$ из $n$ по $k$, используя рекурсивное определение
$C_n^k = \left \{ \begin{array}{l}1, \mbox{ если } k = 0 \mbox{ или } k = n \m......< n, \\\mbox{не определено, в остальных случаях } \\\end{array} \right.$

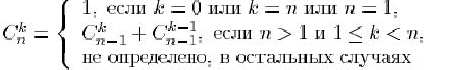
18. Функция Бесселя $J_{n+1}(x)$ порядка $n + 1$ определяется соотношением

$J_{n+1}(x) = \frac{2n}{x} J_n(x) - J_{n-1}(x) (n \geq 2).$

Вычислить $J_{n+1}(x)$ для заданных $n,x,J_o(x)$ и $J_1(x)$, используя рекурсивную функцию Паскаля.

19. Разбиением целого положительного числа $n$ называется его представление в виде суммы целых положительных чисел. При этом два разбиения, отличающихся только порядком слагаемых, различными не считаются. Например, вот все различные разбиения числа 4:
$4, 3+1, 2+2, 2+1+1, 1+1+1+1.$

Для функции $f(n,m)$ -- количества разбиения числа $n$ при условии, что каждое слагаемое не превосходит $m$ -- можно дать следующее определение:

$f(n,m) = \left \{ \begin{array}{l}1, \mbox{ если } n = 1 \mbox{ или } m = 1 ...... = m, \\f(n,m-1) + f(n-m,n), \mbox{ если } n > m. \\\end {array} \right.$

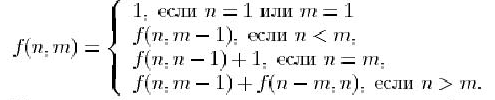
Проверьте правильность этого определения и найдите количество разбиений числа 20, используя рекурсивную функцию для вычисления $f$.

20. Напишите рекурсивную процедуру, которая выдает все различные разбиения (см. предыдущее упражнение) заданного целого положительного числа.

21. Напишите программу без операторов цикла, которая решает задачу нахождения

(1) минимального элемента,
(2) максимального элемента,
(3) максимального и минимального элементов заданной последовательности вещественных чисел.

22. Напишите рекурсивную процедуру или функцию, которая по заданному целому числу $n$

(1) печатает его десятичное представление, используя оператор вывода Write только для печати цифр,
(2) находит сумму цифр, десятичного представления числа,
(3) проверяет, является ли двоичное представление числа симметричной последовательностью,
(4) находит разложение числа на простые сомножители.

23. Реализуйте алгоритм "сортировки слиянием" целочисленного массива длины 100 с помощью рекурсивной процедуры. Алгоритм состоит в том, что массив делится на две половинки, каждая половинка, содержащая более одного элемента, подвергается той же процедуре сортировки слияниями, после чего упорядоченные половинки "сливаются" в единый упорядоченный массив.

24. Проверьте, являются ли эквивалентными следующие два определения:

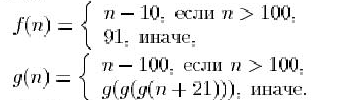
25. Постройте таблицу значений функции

$f(n) = \left \{\begin{array}{l}2, \mbox{ если } n = 0 \mbox{ или } n = 1, \\......ot f(n-2)) \ {\bf div}\ \ 5,\mbox{ если } n\geq 2, \\\end {array} \right.$

для всех $n = 10, 11,\ldots, 20.$

26. Построить синтаксический анализатор для понятия, определяемого следующими синтаксическими правилами:

(1) СКОБКИ=[("["|"(")СКОБКИ СКОБКИ ("["|"(")].
(2) СПИСОК=("A"|"B"){("," | ";") СПИСОК}.
(3) ЗАИКА=за {за} и {и} ка {ка}.

Анализатор должен вводить исходный текст и либо печатать сообщение о том, что этот текст порождается соответствующим понятием, либо (хотя бы одну) причину, по которой текст не может порождаться понятием.

27. Задана последовательность целых неотрицательных чисел. Подсчитать длину ее наибольшей подпоследовательности, состоящей из

(1) полных квадратов,
(2) степеней пятерки,
(3) простых чисел,
(4) чисел, двоичные представления которых содержат нечетное число единиц,
(5) чисел, в десятичной записи которых есть нечетные числа,
(6) чисел, десятичные записи которых являются симметричными цепочками.

В решении использовать функцию, проверяющую соответствующее свойство заданного числа: полный квадрат, степень пятерки и т.д.

28. Найти площадь заданного координатами вершин выпуклого $n$-угольника с использованием функции для вычисления площади треугольника по заданным координатам его вершин.

29. Множество константных формул определяется по следующим двум правилам:

1) любая целочисленная константа является константной формулой;
2) если $T_1$ и $T_2$ являются константными формулами, то константными формулами являются также $(T_1)$, $-T_1$ и $T_1 \oplus T_2$, где $\oplus$ -- любая из арифметических операций $+, -, *,$div, mod.
Написать рекурсивную функцию для вычисления

(1) заданной константной формулы,
(2) по заданной константной формуле $T$ значения $s(T)$, удовлетворяющего следующим соотношениям: $s(T) = \left \{ \begin{array}{l}0, \mbox{ если } T \mbox{ --- число,}\\\ma...... T_1\oplus T_2,\\s(T_1)+1, \mbox{ если } T = (T_1).\\\end{array} \right.$

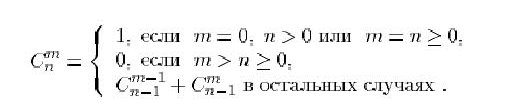
30. Множество простых формул определяется по следующим двум правилам:

1) любая целочисленная константа или идентификатор является простой формулой;
2) если $F_1$ и $F_2$ являются простыми формулами, то простыми формулами являются также $(F_1)$ и $F_1 \oplus F_2$, где $\oplus$ -- любая из арифметических операций $+, -, *,$div, mod.
Префиксная и постфиксная формы записи простых формул определяются по следующим правилам

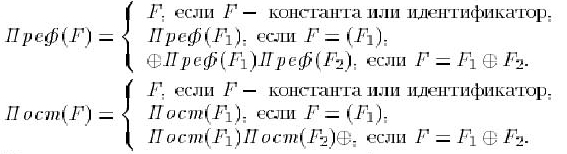
Написать рекурсивную процедуру или функцию для

(1) вычисления простой формулы, не содержащей идентификаторов и представленной в префиксной форме,
(2) преобразует префиксную форму простой формулы в ее постфиксное представление,
(3) восстанавливает простое выражение по ее префиксной записи.

31. Написать рекурсивную функцию для нахождения биномиальных коэффициентов, пользуясь их определением:

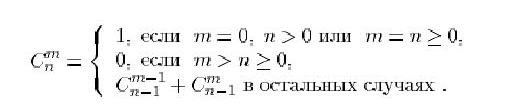
Вычислить $C^k_{2^k}$ для $k=2,4,6,8$.

32. Задано конечное множество имен жителей некоторого города, причем для каждого из жителей перечислены имена его детей. Жители $X$ и $Y$ называются родственниками, если один из них является сыном другого или существует некий житель такой, что он является родственником как $X$, так и $Y$. Перечислить все пары жителей города, которые являются родственниками.

33. Подсчитать количество различных представлений заданного натурального $n$ в виде суммы не менее двух попарно различных положительных слагаемых. Представления, отличающиеся лишь порядком слагаемых, различными не считаются.

34. Напечатать поле для игры в шахматы, в котором черные поля изображаются квадратами, заполненными $5 \times 5=25$ звездочками (символами '*').

35. Вычислить определитель заданной матрицы размера n$\times$n, пользуясь формулой разложения по первой строке: $det (A) =\Sigma_{k=1}^n(-1)^{k+1}a_{1k}*det(B_k)$,
где матрица $B_k$ -- это матрица размера (n-1)$\times$(n-1), которая получается из $A$ вычеркиванием первой строки и $k$-го столбца, если для матрицы $A=(a)$ размера 1$\times$1 детерминант $det(A)$ равен $a.$

36. Напишите две функции вычисления $i$-го числа Фибоначчи -- рекурсивную и нерекурсивную -- и напечатайте таблицу для сравнения времен вычисления $i$-го числа Фибоначчи для $i=4,6,8,10,12$ с помощью этих функций. Используйте для этого стандартную функцию CLOCK -- функцию без параметров, которая выдает целое число, равное времени (в миллисекундах) центрального процессора, уже использованного Zonnon-программой.

37. Функция $f(n)$ определена для целых положительных чисел следующим образом:

$$f(n)= \left \{\begin{array}{ll}1, & \mbox{если } n=1, \\ ......n_{i=2} f([n/i]), & \mbox{если } n\geq 2.\end{array} \right.$$

Вычислить $f(k)$ для $k=15,16,\ldots,30$.

38. Используя рекурсивную процедуру, распечатать на устройстве вывода следующую картинку:

AAAAAAAAAA ................ AAAAAAAAAA  (120 раз)
BBBBBBBB ................ BBBBBBBB   (116 раз)

                                                                                                   ...         ZZ ... ZZ                 (20 раз)                                                                                                    ... BBBBBBBB ................ BBBBBBBB    (116 раз)
AAAAAAAAAA ................ AAAAAAAAAA  (120 раз)

39. Функция $\Phi$ преобразования текста определяется следующим образом:

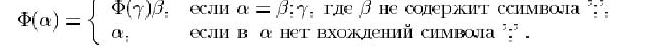
Реализовать функцию $\Phi$ с помощью рекурсивной процедуры.

40. Функция $\Phi$ преобразования вектора целых $\alpha$ определяется следующим образом:

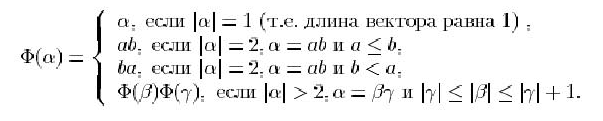
Отметим, что функция $\Phi$ преобразует вектор, не меняя его длину. Реализовать функцию $\Phi$ с помощью рекурсивной процедуры.

П р и м е р: $\Phi$ (1,2,3,4,5,6,7)=1,2,3,4,5,6,7.
 

41. Функция $\Phi$ преобразования вектора целых $\alpha$ определяется следующим образом:

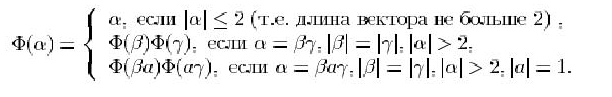
Отметим, что функция $\Phi$ может удлинять вектор. Реализовать функцию $\Phi$ с помощью рекурсивной процедуры.

П р и м е р: $\Phi (1,2,3,4,5,6,7,8,9)=1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9$ 42.

42. Для заданного целого $N$ вычислить значение суммы

$$\sum^N_{i_{1}=1} \sum^N_{i_{2}=1} \ldots \sum^N_{i_{N}=1} \left (\frac{1}{i_1+i_2+ \ldots + i_N} \right )$$

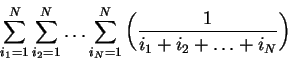
с помощью рекурсивной функции.