6.3 Задания

1. Матрица $C=(c_{ij})$ размера $n$ на $n$ является результатом умножения матрицы $A=(a_{ij})$ на матрицу $B=(b_{ij})$, если для любых $i$,$j$ справедливо равенство $c_{ij}=(\Sigma \ k: 1\leq k\leq n: a_{ik}\cdot b_{kj}).$

Написать процедуру умножения двух вещественных матриц размера (N div 5) + 5 на (N div 5) + 5 и с ее помощью построить (N div 2)+4-ю степень заданной вещественной матрицы.

2. Оформить в виде совокупности процедур и функций решение варианта N + 1 задания 5.7.10, в котором длина заданной последовательности формуляров является параметром, и использовать ее для обработки заданной последовательности пакетов формуляров, где каждый пакет содержит неотрицательное целое число (объем пакета) и последовательность формуляров в количестве, равном объему этого пакета.

3. Решить вариант N + 1 задания 5.7.11 с использованием процедуры ввода всей информации о книгах, процедуры для распечатки каждой из таблиц и функций для проверки различных условий, которым должны удовлетворять книги.

4. Оформить решение варианта N + 1 задания 5.7.13 в виде совокупности процедур и функций и использовать ее для сортировки каждого из наборов сведений об экзаменах из заданной последовательности наборов.

5. Решить вариант N + 1 задания 5.7.15 с использованием процедур ввода и вывода всей информации о деталях, а также функции Паскаля, дающей по номеру элемента в последовательности его номер в результирующей последовательности.

6. Задана последовательность $n$, $a_1,\ldots,a_n,$$m,$$b_1,\ldots,b_m,$$k,$$c_1,$$\ldots,$$c_k$, в которой $n,m,k$ -- натуральные числа, а $a_1,$$\ldots,$$a_n,$$b_1,$$\ldots,$$b_m,$$c_1,$$\ldots,$$c_k$ -- анкеты студентов (трех команд), каждая из которых содержит литеру факультета ($М$M -- математический, $F$ -- физический, C -- химический), на котором студент учится, а также рост и вес студента. Распечатать первые из 100 анкет той из заданных команд, в которой

    наибольший рост (N4 = 0),
    наибольший вес (N4 = 1),
    наименьший рост (N4 = 2),
    наименьший вес (N4 = 3)

имеет тот из соответствующих трех студентов, каждый из которых при анкетировании своей команды сдал анкету

    первым (N < 15),
    последним (N $\geq$ 15)

среди всех своих товарищей по команде, являющихся

    математиками (N3 = 0),
    физиками (N3 = 1),
    химиками (N3 = 2)

и имеющих

    рост выше 1,95 м (N2 = 0),
    вес меньше 70,5 кг (N2 = 1).
 

7. Заданы по

    строкам (N2 = 0),
    столбцам (N2 = 1)

три литерные матрицы размером 30N на 30N. Распечатать их в порядке

    неубывания (N4 < 2),
    невозрастания (N4 $\geq$ 2)
количеств

    букв (N8 < 4),
    цифр (N8 $\geq$ 4),
расположенных в матрице

    над главной (N4 = 0),
    под побочной (N4 = 1),
    под главной (N4 = 2),
    над побочной (N4 = 3)

диагональю.

8. Дана последовательность A,B,C состоящая из трех литерных матриц размером 10N на 10N, заданных по

    строкам (N2 = 0),
    столбцам (N2 = 1).

Вычислить $T_N(A,B,C) = G_{N3}(F_{N5}(A), F_{N5}(B), F_{N5}(C))$, где $G_{N3}$ и $F_{N5}$ обозначают функции, определяемые по следующим правилам для любых целых $х, y, z$ и литерной матрицы $W$:

$G_0(x,y,z) = \min(x,y,z)$,
$G_1(x,y,z) = \max(x,y,z)$,
$G_2(x,y,z) = (x<y) \land (y<z)$,
$F_0(W)$ -- число нечетных цифр, расположенных в $W$ под главной диагональю,
$F_1(W)$ -- число букв $'X','Y'$ и $'Z'$, расположенных в $W$ над побочной диагональю,
$F_2(W$) -- количество столбцов матрицы $W$, не содержащих четных цифр,
$F_3(W)$ -- максимальный номер строки матрицы $W$, состоящей из одних букв, либо ноль, если в $W$ нет буквенных строк,
$F_4(W)$ -- минимальный номер столбца матрицы $W$, содержащего наибольшее количество нечетных цифр.

9. Имеется последовательность матриц $А_1,А_2,А_3,А_4$, в которой каждая $A_i$ -- это целочисленная матрица размером 20N на 20N, заданная по

    строкам (N < 15),
    столбцам (N $\geq 15$).
Вычислить

$T_N(A_1,A_2,A_3,A_4) = \left \{ \begin{array}{l}Q_{N2}(A_1,A_2), \mbox{ если......(A_1,A_2,A_3,A_4),\\Q_{N2}(A_3,A_4) \mbox{ иначе,} \\\end{array} \right.$

где $R_N(A_1,A_2,A_3,A_4)$ = $G_{N3}(P_{N4}(F_{N5}(A_1),$$F_{N5}(A_2)),$$P_{N4}(F_{N5}(A_3),$$F_{N5}(A_4)))$, а $Q_{N2}, P_{N4}, G_{N3}$ и $F_{N5}$ обозначают функции, определяемые по следующим правилам для любых целых чисел $n,m,i,j$, логических значений $x,y,z,w$ и целочисленных матриц B$В=(b_{ij}),$C$С=(c_{ij})$:

$Q_0(B,C) = D$, элемент $d_{ij}$ в которой равен $b_{ij} + c_{ij}$,
$Q_1(B,C) = D$, элемент $d_{ij}$ в которой равен $b_{ij}\cdot c_{ij}$, $G_0(x,y,z,w) = (x \rightarrow y) \lor (z \rightarrow w)$, $G_1(x,y,z,w) = (x \land y) \rightarrow (z \lor w)$,
$G_2(x,y,z,w) = (x \land y \land z) \rightarrow w$,
$P_0(n,m) = n < m$,
$P_1(n,m) = n = m$,
$P_2(n,m) = 2n > 3m$,
$P_3(n,m) = (n + m) > N$,
$F_0(B)$ -- сумма элементов матрицы B$В$, расположенных под побочной диагональю,
$F_1(B)$ -- количество строк матрицы B$В$, состоящих из четных чисел,
$F_2(B)$ -- сумма нечетных элементов матрицы B$В$, расположенных над главной диагональю,
$F_3(B)$ -- число элементов матрицы $В$B, равных сумме своих координат в B$В$,
$F_4(B)$ -- количество столбцов матрицы B, в которых числа расположены в порядке возрастания.

10. Написать функцию, которая по заданной целочисленной матрице $A$ размера $m\times m$, где $m=10N$, вычисляет значение $f(A)$, равное

    сумме (при N2 = 0),
    произведению (при N2 = 1),

номеров таких

    строк (при N4 $<$ 2),
    столбцов (при N4 $\geq$ 2),

матрицы $A$, элементы которых

    попарно различны (при N3 = 0),
    упорядочены по неубыванию (при N3 = 1),
    упорядочены по невозрастанию (при N2 = 2).

С использованием этой функции найти в заданной последовательности матриц $A_1, A_2,$$\ldots,$$A_n,$$\ldots$

    первую (при N6 < 3),
    последнюю (при N6 $\geq$ 3)

такую $A_i$, для которой

    максимально (при N8 < 4),
    минимально (при N8 $\geq$ 4)

значение $f(A_i)+i$mod$N$. Ввод и печать матрицы оформить в виде процедур.

11. Назовем $m$-предложением литерный массив длины $m$, $(n,m)$-страницей -- массив $m$-предложений, $(k,n,m)$-книгой -- массив $(n,m)$-страниц. Рассмотрим следующие две функции:
1) $f(K)$ определяет

    произведение (при N2 = 0),
    сумму (при N2 = 1)

номеров всех тех страниц в книге $K$,

    каждое (при N3 = 0),
    хотя бы одно (при N3 = 1),
    ровно одно (при N3 = 2)

предложение которой является симметричным словом,
2) $g(K,i)$ определяет

    наибольший (при N4 < 2),
    наименьший (при N4 $\geq$ 2)

номер такого предложения на $i$-странице книги $K$, в котором

    нет повторных вхождений букв (при N6 < 3),
    авные количества вхождений букв (при N6 $\geq$ 3).

Из заданной последовательности $(5N, 10N, 20N)$-книг распечатать все те книги, которые

    предшествуют (при N8 < 4),
    следуют за (при N8 $\geq$ 4)
первой такой книгой $K$, для которой

$f(K)=\max g(K,i)$ (при N10 < 5),
$f(K)=\min g(K,i)$ (при N10 $\geq$ 5).

12. В качестве разделителя идентификаторов рассматривается

    пробел (при N2 = 0),
    запятая (при N2 = 1).

Написать функцию, не использующую массивов и циклов, которая по заданной последовательности идентификаторов, после каждого из которых следует ровно один разделитель, находит номер

    первого (при N4 < 2),
    последнего (при N4 $\geq$ 2)
идентификатора, в котором

    сумма (при N3 = 0),
    произведение (при N3 = 1),
    количество (при N3 = 2)

всех кодов

    букв (при N6 $<$ 3),
    цифр (при N6 $\geq$ 3)
является

    максимальным (при N8 < 4),
    минимальным (при N8 $\geq$ 4).

13. Пусть множество ограничителей определено как множество всех

    четных (при N2 = 0),
    кратных трем (при N2 = 1)

целых чисел и задана последовательность целых чисел, завершающаяся ограничителем. Среди всех максимальных подпоследовательностей соседних элементов, не содержащих ограничителей, найти первую такую, номер которой

    меньше (при N4 < 2),
    больше (при N4 $\geq$ 2)
суммы

    квадратных корней (при N3 = 0),
    синусов (при N3 = 1),
    логарифмов (при N3 = 2)

всех
    положительных (при N6 < 3),
    квадратов (при N6 $\geq$ 3)
тех ее элементов, двоичное представление которых содержит

    больше (при N8 < 4),
    меньше (при N8 $\geq$ 4)
$10N$ единиц. Программа не должна содержать массивов и циклов. Она либо распечатывает элементы найденной подпоследовательности в обратном порядке, либо сообщает, что подпоследовательности с указанными свойствами в исходной последовательности нет.

14. Описать рекурсивную функцию, которая для натурального $n$ находит количество целых чисел из отрезка $[0 : 6^n]$, дающих при делении на 6 остаток N6 и сумма цифр пятеричного представления которых дает остаток N5 при делении на 5.

15. Оформить решение варианта N+1 задания 5.7.1 в виде программы без циклов и массивов.

16. Составить программу без циклов и массивов для решения варианта N+1 задания 5.7.2.

17. Решить вариант N+1 задания 5.7.3 в виде программы без циклов и массивов.

18. Составить программу без циклов и массивов для решения варианта N+1 задания 5.7.4.

19. Задан текст -- последовательность литер. Распечатать его, обращая каждую групп из (N+5) следующих друг за другом литер, т.е. печатая литеры этой группы в обратном порядке. Последнюю групп обращать, даже если она содержит менее (N+5) литер. В программе не должно быть циклов.

20. Задана последовательность

    литер (N4 = 0),
    целых чисел (N4 = 1),
    логических значений (N4 = 2),
    вещественных чисел (N4 = 3).

Написать программу, которая распечатывает последовательность, повторяя каждый ее (N30+1)-й элемент N раз, а затем снова печатает все элементы исходной последовательности, но в обратном порядке. В программе не должно быть циклов.

21. Используя рекурсивную функцию, вычислить для заданного $m$ значение суммы

$$\sum_{i_1=1}^N\sum_{i_2=1}^N \ldots\sum_{i_m=1}^N \frac{n}{N+i_1+ i_2+ \ldots + i_m}.$$

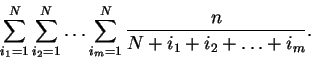
22. Используя рекурсивную функцию, вычислить количество представлений заданного натурального числа в виде суммы

    произвольного количества (N3 = 0),
    не более N+10 (N3 = 1),
    ровно N2+5 (N3 = 2)

слагаемых, каждое из которых положительно и

    кратно трем (N4 = 0),
    не превосходит N+8 (N4 = 1),
    четно (N4 = 2),
    нечетно (N4 = 3).

При этом два представления, различающиеся лишь порядком слагаемых, считаются

    различными (N2 = 0),
    одинаковыми (N2 = 1).

23. Написать рекурсивную функцию вычисления определителя для матриц $A=(a_{ij})$ размером не более $14\times 14$ и таких, что $a_{ij}=0$ для $j=i+N3$ и $i>j+N4.$ При вычислении использовать формулу разложения

    по первой строке (N5 = 0),
    по последней строке (N5 = 1),
    по первому столбцу (N5 = 2),
    по последнему столбцу (N5 $>$ 2).

С помощью этой функции вычислить определитель матрицы $A=(a_{ij})$ размера $(N7+8)\times (N7+8)$, в которой ненулевые околодиагональные элементы $a_{ij}$ равны $j\cdot 2^i+N\cdot (i-j).$
 

© В.Н. Касьянов, Е.В.Касьянова, 2004