Next:6.2.6
Упражнения
Up:6.2
Построение программ с процедурами и функциями
Previous:6.2.4
Быстрая сортировка
Вычислить ![]() для заданного
для заданного ![]() .
.
Решение. Определение чисел Фибоначчи допускает переписывание в виде функции на языке Zonnon, так что мы сразу получаем первое решение
module ФИБ1;
var N: integer;
procedure ФИБ(N:integer):integer;
begin if (N=1) or (N=2) then
return 1(* =![]() (N)
*)
(N)
*)
else return ФИБ(N-1) + ФИБ(N-2) (*=![]() (N)*)
(N)*)
end ФИБ;
begin read(N); writeln('![]() (',N,')=',
ФИБ(N)) end ФИБ1.
(',N,')=',
ФИБ(N)) end ФИБ1.
Однако такая программа неэффективна, она даже при небольших N выполняет слишком много сложений (см. п. 7.2.1). Для написания более эффективной программы введем в рассмотрение функцию
![]() ,
,
которая в качестве результата дает пару целых чисел -- двух соседних элементов последовательности Фибоначчи. Это определение можно переписать в следующем виде
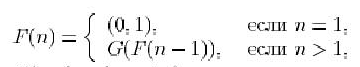
![]() ,
,
если доопределить ![]() .
Тогда
.
Тогда ![]() = Второй
= Второй![]() ,
где Второй
,
где Второй![]() означает
функцию извлечения второго элемента пары.
означает
функцию извлечения второго элемента пары.
Такое определение нельзя сразу переписать в виде функций языка Zonnon, поскольку в нем все функции должны иметь скалярные результаты. Однако мы можем хранить эту пару в глобальных переменных A,B.
module ФИБ2;
var A,B,N : integer;
procedure ФИБ (N:Integer);
var C:integer;
begin
if N = 1 then
A := 0; B := 1 (*![]() *)
end
*)
end
else ФИБ(N-1); (*![]() *)
*)
C := A+B; A := B; B := C (*![]() *)
*)
end
end ФИБ ;
begin
read(N);
ФИБ(N); (* {A = ![]() (N-1),
B =
(N-1),
B = ![]() (N)}
*)
(N)}
*)
writeln('![]() (',N,')=',B)
(',N,')=',B)
end ФИБ2.
Можно заметить, что смысл программы не изменится, если локальную переменную С процедуры ФИБ объявить в теле программы. После этого рекурсия процедуры ФИБ будет использоваться исключительно для тогo, чтобы повторять последовательность операторов
begin C := A+B; A := B; B := C end.
Это повторение записывается на языке Zonnon с помощью оператора цикла, так что в нашем третьем решении мы элиминируем рекурсию, программа ФИБ3 вовсе не будет содержать процедур и функций:
module ФИБ3;
var A,B,C,N,I : Integer;
begin
Read(N); A := 0; B := 1; (*![]() *)
*)
for I := 2 to N do
(* {A=Ф(I-2),
B= Ф(I-1)}*)
C := A+B; A := B;
B := C (* {A=Ф(I-1), B= Ф(I)}*)
end;
(*{B=C=Ф(N)}*)
writeln ('Ф(',N,')=',B)
end ФИБ3.
Для получения четвертого решения заметим, что записанное выше определение
функции ![]() ,
преобразующей пары целых чисел снова в пары целых чисел, можно переписать
с использованием операции произведения матрицы на вектор, а именно
,
преобразующей пары целых чисел снова в пары целых чисел, можно переписать
с использованием операции произведения матрицы на вектор, а именно
![]()
Это значит, что ![]() ,
а для возведения матрицы
,
а для возведения матрицы ![]() в целую степень можно использовать, по-существу, тот же самый алгоритм
быстрого возведения в степень, что и для возведения в степень обычных чисел.
в целую степень можно использовать, по-существу, тот же самый алгоритм
быстрого возведения в степень, что и для возведения в степень обычных чисел.
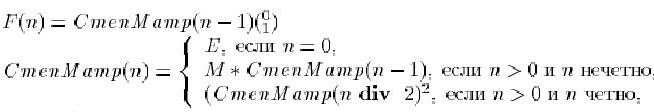
![]()
![]()
Можно заметить, что для ![]()
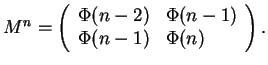
так что мы можем представлять матрицу ![]() парой чисел -- ее первой строкой. В таком представлении упрощается операция
произведения матриц:
парой чисел -- ее первой строкой. В таком представлении упрощается операция
произведения матриц: ![]() С учетом сказанного получаем следующую программу:
С учетом сказанного получаем следующую программу:
module ФИБ4;
type MATR = array 2 of Integer;
var K,N : Integer; X,Y : MATR;
procedure MULT (X,Y : MATR; var Z
: MATR);
var T : integer;
begin
T := X[1] ![]() Y[1]; Z[0]:= X[0]
Y[1]; Z[0]:= X[0]![]() Y[0]+T;
Y[0]+T;
Z[1]:= X[0] ![]() Y[1]+ X[1]
Y[1]+ X[1]![]() Y[0] + T
Y[0] + T
end MULT;
begin
Read(N); X[0]:= 0; X[1]:= 1; Y[0]:= 1; Y[1]:= 0;
K := N;
while N # 0 do
if odd(N) then
MULT(Y,X,Y); N := N-1 else MULT(X,X,X); N := N div 2 end
end;
writeln('Ф(',K,')=',Y.B)
end ФИБ4.
Для получения рекурсивного решения без излишних сложений рассмотрим следующую функцию (см. ФИБ3) :
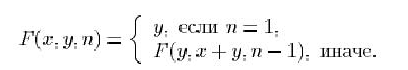
Очевидно, что ![]() ,
и мы приходим к следующему рекурсивному решению, которое в отличие от ФИБ1
уже не содержит повторных вычислений членов последовательности:
,
и мы приходим к следующему рекурсивному решению, которое в отличие от ФИБ1
уже не содержит повторных вычислений членов последовательности:
module ФИБ5;
var N: Integer;
procedure F(X, Y, M, N:Integer):Integer;
begin if N=1
then
return Y else return F(Y, X+Y, N-1) end end F;
begin read(N); writeln('![]() (',N,')=',
F(0,1,N)) end ФИБ5.
(',N,')=',
F(0,1,N)) end ФИБ5.
Next:6.2.6
Упражнения
Up:6.2
Построение программ с процедурами и функциями