Разбиение схемы: сбалансированный подход с минимальным разрезом на базе сетевого потока
Ключевые слова и синонимы
Разбиение гиперграфа; разбиение таблицы соединений
Постановка задачи
Разбиение схемы является фундаментальной задачей в сфере проектирования и разработки СБИС. Сбалансированное биразбиение с минимальным разрезом представляет собой задачу разбиения схемы на два отдельных компонента с равными весами, такого, что количество сеток, соединяющих эти два компонента, минимально. Было показано, что задача сбалансированного биразбиения с минимальным разрезом является NP-полной [5]. Эта задача была решена при помощи эвристических алгоритмов, таких как методы итеративного улучшения Кернигана и Лина (эвристика K&L) [4, 11], алгоритм имитации отжига [10] и аналитические методы для рационального разреза [2, 7, 13, 15]. Несмотря на то, что техника нахождения максимального потока и минимального разреза [6, 8] представляется естественным способом поиска минимального разреза, она практически не использовалась в контексте разбиения схем. В работе [16] был предложен метод точного моделирования таблицы соединений сети (или, что эквивалентно, ее гиперграфа) при помощи транспортной сети, а также алгоритм нахождения сбалансированного биразбиения на основе неоднократного применения алгоритма нахождения максимального потока и минимального разреза. Представленный здесь алгоритм имеет ту же асимптотическую сложность, что и вычисление минимального потока.
Алгоритм сбалансированного биразбиения на базе потока (Flow-Balanced-Bipartition, FBB)
1. выбрать пару вершин s и t в N;
2. найти минимальный сетевой разрез C в N;
пусть X – подсхема, достижимая из s по дополняющим путям в транспортной сети, а [math]\displaystyle{ \bar{X} }[/math] – остальная часть схемы;
3. if [math]\displaystyle{ (1 - \epsilon)rW \le w(X) \le (1 + \epsilon)rW \; }[/math]
вернуть C в качестве ответа;
4. if [math]\displaystyle{ w(X) \lt (1 - \epsilon)rW \; }[/math]
4.1. сколлапсировать все вершины в X с s;
4.2. выбрать вершину [math]\displaystyle{ v \in \bar{X} }[/math], смежную с C, и сколлапсировать ее с s;
4.3. перейти к 1;
5. if [math]\displaystyle{ w(X) \gt (1 + \epsilon)rW \; }[/math]
5.1. сколлапсировать все вершины в [math]\displaystyle{ \bar{X} }[/math] с t;
5.2. выбрать вершину [math]\displaystyle{ v \in X \; }[/math], смежную с C, и сколлапсировать ее с t;
5.3. перейти к 1;
Рисунок 1. Алгоритм FBB
Процедура инкрементного вычисления потока
1. while [math]\displaystyle{ \exists }[/math] добавочный дополняющий путь из s в t увеличить величину потока вдоль дополняющего пути; 2. пометить все вершины u, такие, что [math]\displaystyle{ \exists }[/math] дополняющий путь из s в u; 3. пусть C' – множество мостовых ребер, начальные вершины которых помечены, а концевые – не помечены; 4. вернуть сетки, соответствующие мостовым ребрам в C', в качестве минимального сетевого разреза C, а помеченные вершины – в качестве X.
Рисунок 2. Инкрементное вычисление потока
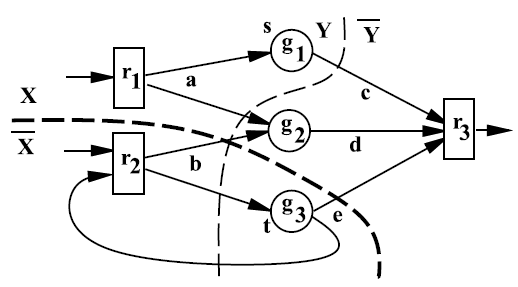
Рисунок 3. Таблица соединений схемы с двумя сетевыми разрезами
Таблица соединений схемы определяется как орграф N = (V, E), где V – множество вершин, представляющих логические вентили и регистры, а E – множество ребер, представляющих провода между вентилями и регистрами. Каждая вершина [math]\displaystyle{ v \in V \; }[/math] имеет вес [math]\displaystyle{ w(v) \in R^+ \; }[/math]. Общий вес подмножества [math]\displaystyle{ U \subseteq V \; }[/math] определяется как [math]\displaystyle{ w(U) = \sum_{v \in U} w(v) \; }[/math]. W = w(V) обозначает полный вес схемы. Сетка [math]\displaystyle{ n = (v; v_1, ..., v_l) \; }[/math] представляет собой множество ребер, исходящих из вершины v в N. Пусть даны две вершины s и t в N; s-t-разрез (далее для краткости просто «разрез») [math]\displaystyle{ (X, \bar{X}) \; }[/math] графа N представляет собой биразбиение вершин V, такое, что [math]\displaystyle{ s \in X \; }[/math] и [math]\displaystyle{ t \in \bar{X} \; }[/math]. Сетевым разрезом [math]\displaystyle{ net(X, \bar{X}) \; }[/math] разреза является множество сеток в N, инцидентных вершинам одновременно в [math]\displaystyle{ X \; }[/math] и [math]\displaystyle{ \bar{X} \; }[/math]. Разрез [math]\displaystyle{ (X, \bar{X}) \; }[/math] является минимальным сетевым разрезом, если значение [math]\displaystyle{ |net(X, \bar{X})| \; }[/math] минимально среди всех s-t-разрезов N. На рис. 3 представлены сетка [math]\displaystyle{ a = (r_1; g_1, g_2) \; }[/math], сетевые разрезы [math]\displaystyle{ net(X, \bar{X}) = \{ b, e \} \; }[/math] и [math]\displaystyle{ net(Y, \bar{Y}) = \{ c, a, b, e \} \; }[/math] и минимальный сетевой разрез [math]\displaystyle{ (X, \bar{X}) \; }[/math].
Говоря формально, пусть даны пропорция [math]\displaystyle{ r \; }[/math] и коэффициент отклонения [math]\displaystyle{ \epsilon \; }[/math]. Задача r-сбалансированного биразбиения с минимальным разрезом заключается в нахождении биразбиения [math]\displaystyle{ (X, \bar{X}) \; }[/math] таблицы соединений N, такого, что:
(1) [math]\displaystyle{ (1 - \epsilon) rW \le W(X) \le (1 + \epsilon) rW \; }[/math];
(2) размер разреза [math]\displaystyle{ net(X, \bar{X}) \; }[/math] минимален среди всех разрезов, удовлетворяющих условию (1).
Если r = 1/2, задача превращается в задачу сбалансированного биразбиения с минимальным разрезом.
Основные результаты
Биразбиение с минимальным сетевым разрезом на базе оптимального сетевого потока
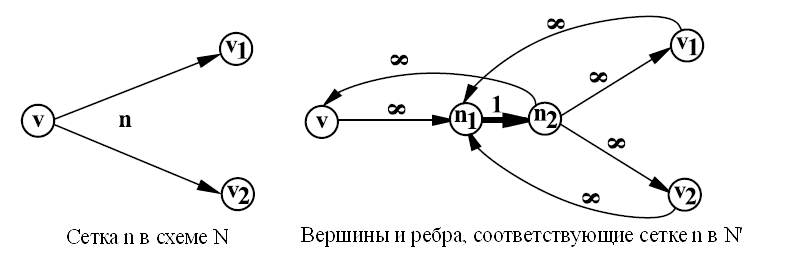
Задача нахождения минимального сетевого разреза в N = (V, E) сводится к задаче нахождения разреза минимальной пропускной способности, которая решается при помощи техники вычисления максимального потока и минимального разреза. Транспортная сеть N' = (V', E') строится из N = (V, E) следующим образом (см. рис. 4 и 5):
1. V' содержит все вершины из V.
2. Для каждой сетки [math]\displaystyle{ n = (v; v_1, ..., v_l) \; }[/math] в N добавить две вершины [math]\displaystyle{ n_1 \; }[/math] и [math]\displaystyle{ n_2 \; }[/math] в V' и мостовое ребро [math]\displaystyle{ bridge(n) = (n_1, n_2) \; }[/math] в E'.
3. Для каждой вершины [math]\displaystyle{ u \in \{ v; v_1, ..., v_l \} \; }[/math], инцидентной сетке n, добавить два ребра [math]\displaystyle{ (u, n_1) \; }[/math] и [math]\displaystyle{ (n_2, u) \; }[/math] в E'.
4. Положить s источником N', а t – стоком N'.
5. Присвоить единичную пропускную способность всем мостовым ребрам и бесконечную пропускную способность – всем остальным ребрам в E'.
6. Для вершины [math]\displaystyle{ v \in V\ \; }[/math], соответствующей вершине в V, w(v) обозначает вес v в N. Для вершины [math]\displaystyle{ u \in V' \; }[/math], отщепленной от сетки, w(u) = 0.
Рисунок 4. Моделирование сетки в N в транспортной сети N'
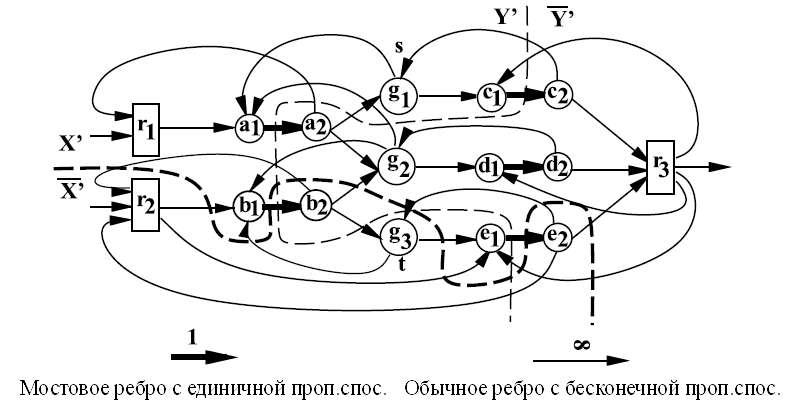
Рисунок 5. Транспортная сеть для рис. 3
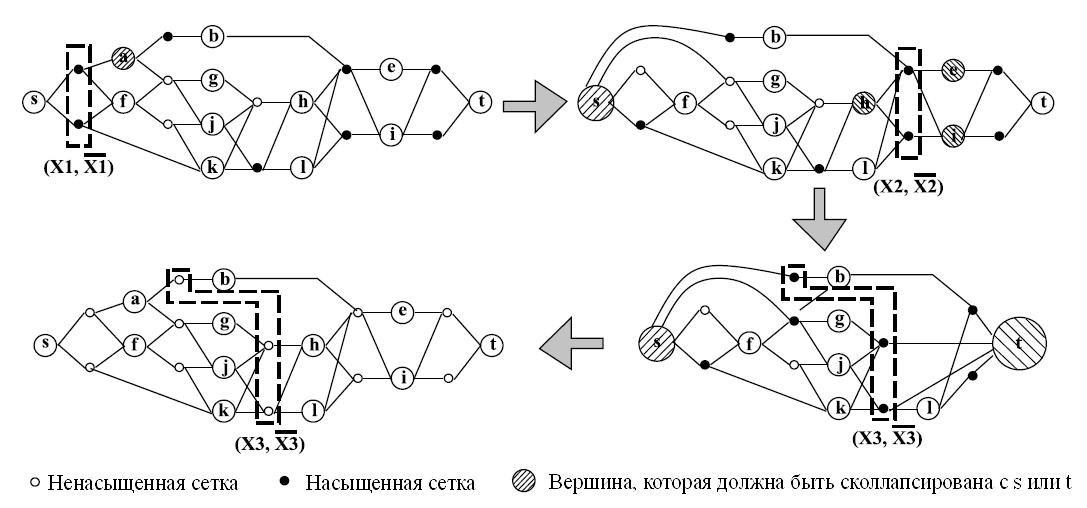
Рисунок 6. Алгоритм FBB для примера на рис. 5 для значений r = 1/2, [math]\displaystyle{ \epsilon \; }[/math] = 0,15 и единичного веса каждой вершины. Алгоритм завершает работу после нахождения разреза [math]\displaystyle{ (X_2, \bar{X_2}) \; }[/math].
Маленькая черная вершина обозначает, что мостовое ребро, соответствующее сетке, насыщено потоком
Таблица 1. Сравнение алгоритмов SN, PFM3 и FBB (r = 1/2, [math]\displaystyle{ \epsilon \; }[/math] = 0,1)
| Схема | Средний размер сетевого разреза | Биразбиение FBB | Улучшение (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Название | Вентили и триггеры | Сетки | Средн. степ. | SN | PFM3 | FBB | (отношение) | К SN | К PFM3 |
| C1355 | 514 | 523 | 3,0 | 38,9 | 29,1 | 26,0 | 1:1,08 | 33,2 | 10,7 |
| C2670 | 1161 | 1254 | 2,6 | 51,9 | 46,0 | 37,1 | 1:1,15 | 28,5 | 19,3 |
| C3540 | 1667 | 1695 | 2,7 | 90,3 | 71,0 | 79,8 | 1:1,11 | 11,6 | -12,4 |
| C7552 | 3466 | 3565 | 2,7 | 44,3 | 81,8 | 42,9 | 1:1,08 | 3,2 | 47,6 |
| S838 | 478 | 511 | 2,6 | 27,1 | 21,0 | 14,7 | 1:1,04 | 45,8 | 30,0 |
| Среднее | 1:1,10 | 24,5 | 19,0 | ||||||
Таблица 2. Сравнение алгоритмов EIG1, PB и FBB (r = 1/2, [math]\displaystyle{ \epsilon \; }[/math] = 0,1). Все допускают отклонение [math]\displaystyle{ \le 10% }[/math]
| Схема | Лучший размер сетевого разреза | Улучшение (%) | FBB продолж. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Название | Вентили и триггеры | Сетки | Средн. степ. | EIG1 | PFB | FBB | К EIG1 | К PB | (сек) |
| S1423 | 731 | 743 | 2,7 | 23 | 16 | 13 | 43,5 | 18,8 | 1,7 |
| S9234 | 5808 | 5805 | 2,4 | 227 | 74 | 70 | 69,2 | 5,4 | 55,7 |
| S13207 | 8696 | 8606 | 2,4 | 241 | 91 | 74 | 69,3 | 18,9 | 100,0 |
| S15850 | 10310 | 10310 | 2,4 | 215 | 91 | 67 | 68,8 | 26,4 | 96,5 |
| S35932 | 18081 | 17796 | 2,7 | 105 | 62 | 49 | 53,3 | 21,0 | 2808 |
| S38584 | 20859 | 20593 | 2,7 | 76 | 55 | 47 | 38,2 | 14,5 | 1130 |
| S38417 | 24033 | 23955 | 2,4 | 121 | 49 | 58 | 52,1 | -18,4 | 2736 |
| Среднее | 58,5 | 11,3 | |||||||
Заметим, что все вершины, инцидентные сетке n, привязаны к [math]\displaystyle{ n_1 \; }[/math], а также к ним привязана [math]\displaystyle{ n_2 \; }[/math] в N'. Следовательно, построение транспортной сети симметрично относительно всех вершин, инцидентных сетке. Это построение можно провести также в случае, если таблица соединений представлена гиперграфом.
Очевидно, что N' является сильно связным орграфом. Это свойство является определяющим для сведения задачи нахождения двунаправленного минимального сетевого разреза к задаче разреза с минимальной пропускной способностью, учитывающей только пропускную способность прямых ребер.
Теорема 1. N имеет разрез величиной не более C в том и только том случае, если N' имеет разрез с пропускной способностью не более C.
Следствие 1. Пусть [math]\displaystyle{ (X', \bar{X'}) \; }[/math] – разрез с минимальной пропускной способностью C в N'. Пусть [math]\displaystyle{ N_{cut} = \{ n | bridge(n) \in (X', \bar{X'}) \} \; }[/math]. Тогда [math]\displaystyle{ N_{cut} = (X, \bar{X}) \; }[/math] является минимальным сетевым разрезом в N и [math]\displaystyle{ |N_{cut}| = C \; }[/math].
Следствие 2. Минимальный сетевой разрез в схеме N = (V, E) можно найти за время O(|V| |E|).
Эвристика для сбалансированного биразбиения с минимальным разрезом
Вначале неоднократно применяется эвристический алгоритм вычисления максимального потока и минимального разреза, затем выполняется сбалансированное биразбиение потока (FBB) для нахождения r-сбалансированного биразбиения, минимизирующего количество пересекаемых сеток. Затем разрабатывается эффективная реализация FBB, имеющая ту же асимптотическую сложность, что и однократное вычисление минимального потока. Ради упрощения представления алгоритм FBB излагается здесь в формулировке для исходной схемы, а не для транспортной сети, построенной из этой схемы. Эвристический алгоритм представлен на рис. 1, на рис. 6 приведен пример использования.
В таблице 2 сравниваются лучшие варианты реализации FBB с точки зрения размеров сетевых разрезов с лучшими вариантами алгоритмов разбиения на базе аналитических методов – EIG1 (Хаген и Канг, [7]) и PARABOLI (PB) (Рисс и др. [13]). Результаты алгоритма PARABOLI ранее были наилучшими известными результатами для эталонных схем. Результаты алгоритма FBB оказались лучшими для десяти прогонов. В среднем FBB превзошел EIG1 и PARABOLI на 58,1% and 11,3%, соответственно. Для схемы S38417 субоптимальный результат FBB может быть улучшен за счет (1) увеличения количества прогонов и (2) применения техник кластеризации к схеме на базе знания имеющихся соединений (до выполнения разбиения).
При реализации алгоритма FBB был выбран метод коллапсирования вершин, а не более постепенный (например, из [9]), чтобы гарантировать, что пропускная способность разреза всегда отражает реальный размер сетевого разреза. При выборе вершины на шагах 4.2 и 5.2 задан порог R для количества вершин в несколлапсированной подсхеме. Вершина выбирается случайным образом, если количество вершин больше R. В противном случае проверяются все вершины, смежные с C, и выбирается та, коллапс которой порождает минимальный сетевой разрез наименьшего размера. Прямолинейная реализация шага 2, заключающаяся в вычислении максимального потока начиная с нулевого, приведет к резкому росту временной сложности. Вместо этого сохраняется значение потока в транспортной сети и исследуется дополнительный поток для насыщения мостовых ребер минимального сетевого разреза между двумя итерациями. Процедура представлена на рис. 2. Вначале сеть потока сохраняет функцию потока, вычисленную на предыдущей итерации. Поскольку вычисление максимального потока при помощи метода приращения путей нечувствительно к изначальным величинам потока и порядку нахождения дополняющих путей, вышеописанная процедура корректно находит максимальный поток с той же величиной потока, что и у максимального потока, вычисленного в коллапсированной транспортной сети из нулевого значения.
Теорема 2. Алгоритм FBB имеет временную сложность O(|V| |E|) для связной схемы N = (V, E).
Теорема 3. Количество итераций и финальный размер сетевого разреза представляют собой невозрастающие функции от [math]\displaystyle{ \epsilon \; }[/math].
На практике алгоритм FBB завершается намного быстрее, чем указывает временная сложность для наихудшего случая, как показано в разделе «Экспериментальные результаты». Теорема 3 позволяет повысить эффективность FBB и качество разбиения для больших значений [math]\displaystyle{ \epsilon \; }[/math]. Это неверно для других подходов к разбиению – таких как эвристика K&L.
Применение
Разбиение схемы является фундаментальной задачей в сфере проектирования СБИС и автоматизации разработки. Алгоритм FBB представляет собой первое эффективное прогнозируемое решение задачи сбалансированного разбиения схемы с минимальным разрезом. Установлена прямая зависимость эффективности и качества решения, производимого алгоритмом, от коэффициента отклонения [math]\displaystyle{ \epsilon \; }[/math]. Алгоритм можно легко расширить для применения к сеткам с различными весами, присваивая вес сетки ее мостовому ребру в транспортной сети. K-стороннее разбиение с минимальным разрезом для K > 2 можно получить при помощи рекурсивного применения FBB либо положив r = 1/K и затем используя FBB для поиска разбиений по одному. Метод прямого решения задачи с использованием потоков приводится в [12]. Кластеризацию схемы перед разбиением с использованием данных о связях или расчетов времени можно легко встроить в алгоритм FBB, рассматривая кластер как вершину. Для дальнейшей настройки решения можно использовать эвристические техники на базе эвристики K&L или алгоритма имитации отжига с низкой температурой.
Экспериментальные результаты
Алгоритм FBB был внедрен в SIS/MISII [1] и протестирован на наборе больших тестовых схем ISCAS и MCNC на рабочей станции SPARC 10 с процессором с тактовой частотой 36 МГц и 32 МБ памяти.
В таблице 1 приводится сравнение средних результатов алгоритма FBB в процессе биразбиения с результатами Дасдана и Эйканата из [3]. SN основан на применении эвристического алгоритма K&L в работе Санчиса [14]. PFM3 основан на применении эвристического алгоритма K&L со свободными перемещениями, как описано в [3]. На каждой схеме SN выполнялся 20 раз, а PFM3 – 10 раз с различными изначальными разбиениями, сгенерированными случайным образом. FBB выполнялся 10 раз с различными случайным образом выбранными s и t. За единственным исключением FBB показал себя лучше SN и PFM3 на пяти схемах. В среднем FBB удалось найти биразбиение с количеством пересечений сеток на 24,5% и 19,0% меньше, чем SN и PFM3, соответственно. Время выполнения алгоритмов SN, PFM3 и FBB не сравнивалось, поскольку они выполнялись на разных рабочих станциях.
См. также
- Приближенное решение задачи о максимальном потоке
- Компоновка схемы
- Ресинхронизация схемы
- Максимальный разрез
- Минимальная бисекция
- Многосторонний разрез
- Сепараторы в графах
Литература
1. Brayton, R.K., Rudell, R., Sangiovanni-Vincentelli, A.L.: MIS: A Multiple-Level Logic Optimization. IEEE Trans. CAD 6(6), 1061-1081 (1987)
2. Cong, J., Hagen, L., Kahng, A.: Net Partitions Yield Better Module Partitions. In: Proc. 29th ACM/IEEE Design Automation Conf., 1992, pp. 47-52
3. Dasdan, A., Aykanat, C.: Improved Multiple-Way Circuit Partitioning Algorithms. In: Int. ACM/SIGDA Workshop on Field Programmable Gate Arrays, Feb. 1994
4. Fiduccia, C.M., Mattheyses, R.M.: A Linear Time Heuristic for Improving Network Partitions. In: Proc. ACM/IEEE Design Automation Conf., 1982, pp. 175-181
5. Garey, M., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman, Gordonsville (1979)
6. Goldberg, A.W., Tarjan, R.E.: A New Approach to the Maximum Flow Problem. J. SIAM 35,921-940 (1988)
7. Hagen, L., Kahng, A.B.: Fast Spectral Methods for Ratio Cut Partitioning and Clustering. In: Proc. IEEE Int. Conf. on Computer-Aided Design, November 1991, pp. 10-13
8. Hu, T.C., Moerder, K.: Multiterminal Flows in a Hypergraph. In: Hu,T.C., Kuh, E.S. (eds.) VLSI Circuit Layout: Theory and Design, pp. 87-93. IEEE Press (1985)
9. Iman, S., Pedram, M., Fabian, C., Cong, J.: Finding Uni-Directional Cuts Based on Physical Partitioning and Logic Restructuring. In: 4th ACM/SIGDA Physical Design Workshop, April 1993
10. Kirkpatrick, S., Gelatt, C.D., Vecchi, M.P.: Optimization by Simulated Annealing. Science 4598,671-680 (1983)
11. Kernighan, B., Lin, S.: An Efficient Heuristic Procedure for Partitioning of Electrical Circuits. Bell Syst. Tech. J., 291-307 (1970)
12. Liu, H., Wong, D.F.: Network-Flow-based Multiway Partitioning with Area and Pin Constraints. IEEE Trans. CAD Integr. Circuits Syst. 17(1), 50-59(1998)
13. Riess, B.M., Doll, K., Frank, M.J.: Partitioning Very Large Circuits Using Analytical Placement Techniques. In: Proc. 31th ACM/IEEE Design Automation Conf., 1994, pp. 646-651
14. Sanchis, L.A.: Multiway Network Partitioning. IEEE Trans. Comput. 38(1), 62-81 (1989)
15. Wei, Y.C., Cheng, C.K.: Towards Efficient Hierarchical Designs by Ratio Cut Partitioning. In: Proc. IEEE Int. Conf. on Computer-Aided Design, November 1989, pp. 298-301
16. Yang, H., Wong, D.F.: Efficient Network Flow Based Min-Cut Balanced Partitioning. In: Proc. IEEE Int. Conf. on Computer-Aided Design, 1994, pp. 50-55