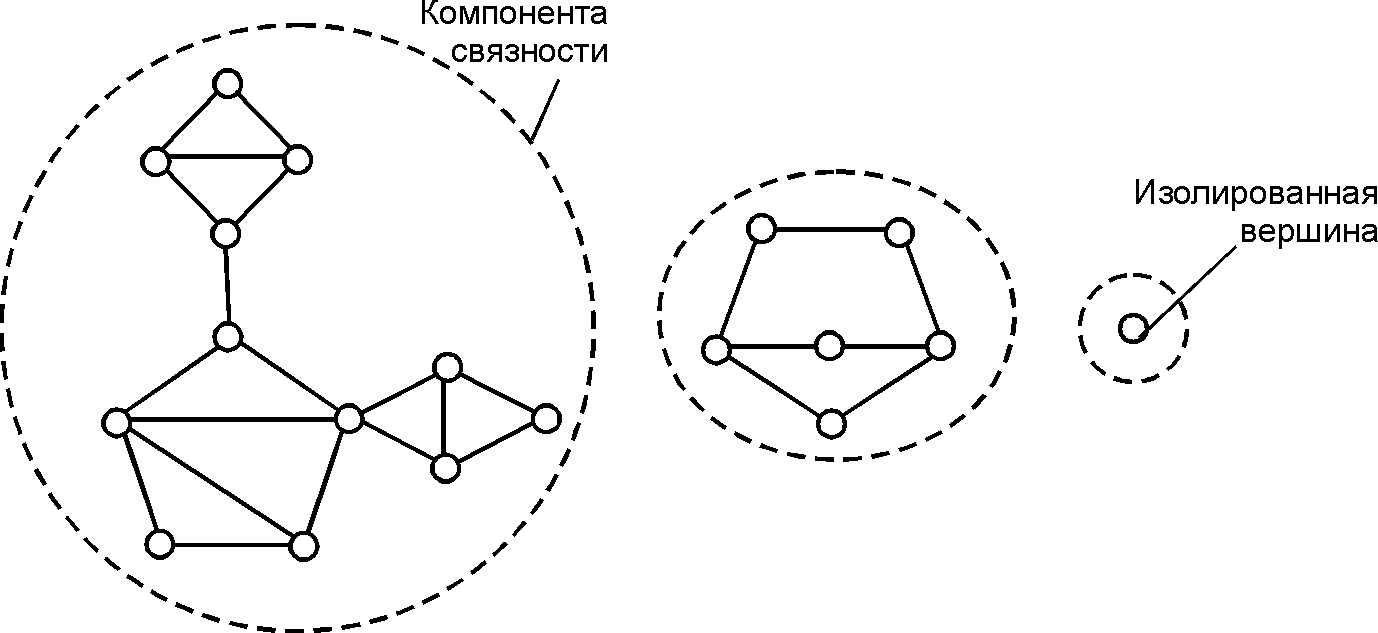
Граф (неориентированный граф)
Граф (неориентированный граф) (Graph (undirected graph)) — это
1. Пара [math]\displaystyle{ (V,E) }[/math], где [math]\displaystyle{ V }[/math] — непустое множество объектов
некоторой природы, называемых вершинами графа, а [math]\displaystyle{ E }[/math] —
подмножество двухэлементных подмножеств множества [math]\displaystyle{ V }[/math], называемых
ребрами графа. Множества вершин и ребер графа [math]\displaystyle{ G }[/math] обозначают
[math]\displaystyle{ V(G) }[/math] и [math]\displaystyle{ E(G) }[/math] соответственно. Если [math]\displaystyle{ |V(G)| = n }[/math] и [math]\displaystyle{ |E(G)| = m }[/math],
то говорят о [math]\displaystyle{ (n,m) }[/math]-графе [math]\displaystyle{ G }[/math].
2. Пара [math]\displaystyle{ (V,E) }[/math], где [math]\displaystyle{ V }[/math] — множество вершин графа, а [math]\displaystyle{ E }[/math] — множество ребер — есть подмножество множества [math]\displaystyle{ V_{-}^{2} / \sim }[/math] классов эквивалентности, на которые множество [math]\displaystyle{ V_{-}^{2} = \{(v,w) | v \neq w \} }[/math] разбивается отношением эквивалентности: [math]\displaystyle{ (v_{1},w_{1}) \sim (v_{2},w_{2}) \Leftrightarrow (v_{1},w_{1}) = (v_{2},w_{2}) }[/math] или [math]\displaystyle{ (v_{1},w_{1}) = (w_{2},v_{2}). }[/math]
3. Тройка [math]\displaystyle{ (V,E,P) }[/math], где [math]\displaystyle{ V }[/math] — множество вершин, [math]\displaystyle{ E }[/math] — множество объектов некоторой природы, отличной от природы вершин, называемых ребрами, [math]\displaystyle{ P }[/math] — инцидентор, сопоставляющий с каждым ребром [math]\displaystyle{ e \in E }[/math] пару граничных вершин [math]\displaystyle{ v }[/math] и [math]\displaystyle{ w }[/math] из [math]\displaystyle{ V }[/math].
4. Общее название как для неориентированного, так и для ориентированного графов.
См. также
- Абстрактный граф,
- Альфа-перестановочный граф,
- Антисимметрический граф,
- Аранжируемый граф,
- Асимметричный граф,
- Бесконечный граф,
- Бесконтурный орграф,
- Бихроматический граф,
- Вершинно-критический граф,
- Вершинно непересекающиеся графы,
- K-вершинно-связный граф,
- Вершинно-симметрический граф,
- Взаимно связный граф,
- Взвешенный граф,
- Внешнепланарный граф,
- Внешнеплоский граф,
- Вполне несвязный граф,
- Выпуклый прямолинейный граф,
- Гамильтонов граф,
- Гамильтоново-связный граф,
- Геодезический граф,
- L-геодезический граф,
- Геометрически двойственный граф,
- Гипогамильтоновый граф,
- Гомеоморфные графы,
- Графы Куратовского,
- Дважды хордальный граф,
- Двойственно хордальный граф,
- Двойственный граф,
- Двудольный граф,
- Двусторонний граф,
- Дистанционно наследуемый граф,
- Дистанционно-транзитивный граф,
- K-дольный граф,
- Звездно-экстремальный граф,
- Звездный граф,
- N-звездный граф,
- Знаковый помеченный граф,
- Изоморфные графы,
- Индифферентный граф,
- Индуктивный граф,
- Информационный граф,
- Конечный граф,
- Гамма-конечный граф,
- Корневой граф,
- Коспектральные графы,
- Критический граф,
- Кубический граф,
- Локально конечный граф,
- Локально ограниченный граф,
- Локально счетный граф,
- Максимальный сильно сингулярный граф,
- Максимальный сингулярный граф,
- Минимально связный граф,
- Многоугольный граф,
- Накрывающий граф,
- K-насыщенный граф,
- Неразделимый граф,
- Неразложимый граф,
- Несводимый граф,
- Несепарабельный граф,
- Нечетный граф,
- Обратный орграф,
- Общий граф,
- Обыкновенный граф,
- Однозначно раскрашиваемый граф,
- Однородный граф,
- Односторонне связный орграф,
- Односторонний орграф,
- Одноциклический граф,
- Ориентированно-циклически замкнутый граф,
- Ориентированный граф,
- Ориентируемый граф,
- Панциклический граф,
- J-панциклический граф,
- Планарный граф,
- Плоский граф,
- (a,b)-плоский граф,
- Покрывающий граф,
- Полный граф,
- Полный двудольный граф,
- Полный k-дольный граф,
- Полугамильтонов граф,
- Полунесводимый граф,
- Полуэйлеров граф,
- Помеченный граф,
- Пороговый граф,
- Почти однородный граф,
- Правильный граф,
- Предельный граф,
- Префиксный граф ширины n,
- Прогрессивно конечный граф,
- Прогрессивно ограниченный граф,
- Производный граф,
- Произвольно вычерчиваемый граф,
- Произвольно гамильтонов граф,
- Произвольно проходимый граф,
- Простой граф,
- Прямоугольный граф,
- Псевдосимметрический граф,
- Пустой граф,
- Разборный граф,
- Раскрашенный граф,
- Реберно раскрашиваемый граф,
- K-раскрашенный граф,
- K-раскрашиваемый граф,
- Расщепляемый граф,
- Реберно-критический граф,
- Реберно k-раскрашиваемый граф,
- Расширенный нечетный граф,
- Реберно изоморфные графы,
- Реберно-регулярный граф,
- K-реберно-связный граф,
- Реберно-симметрический граф,
- Реберный граф,
- Регрессивно конечный граф,
- Регрессивно ограниченный граф,
- Регуляризуемый граф,
- Регулярный граф,
- Регулярный степени 0 граф,
- Реконструируемый граф,
- Самодополнительный граф,
- Самонегативный граф,
- Сбалансированный граф,
- Сводимый граф,
- Связный граф,
- K-связный граф,
- Два-секционный граф,
- Сильно ориентированно-циклически замкнутый граф,
- Сильно ориентированно-циклически-реберный граф,
- Сильно связный граф,
- Сильно-циклически замкнутый граф,
- Сильно-циклически связный граф,
- Симметрический граф,
- Сингулярно связные графы,
- Слабо связный граф,
- Слабый орграф,
- Смешанный граф,
- Совершенный граф,
- Соединяющий граф,
- Соотнесенный неориентированный граф,
- Составной граф,
- Степенно-хордальный граф,
- Строго геодезический граф,
- Строго хордальный граф,
- Структурный граф,
- Стягиваемый граф,
- Счетный граф,
- Топологический граф,
- S-топологический граф,
- Тороидальный граф,
- Тотальный граф,
- Транзитивно ориентируемый граф,
- Транзитивный граф,
- K-транзитивный граф,
- Триангулированный граф,
- Тривиальный граф,
- Узловой граф,
- Унитарный граф,
- K-унитранзитивный граф,
- Унициклический граф,
- Упорядоченный граф,
- Управляющий граф,
- Хордальный граф,
- Хордальный двудольный граф,
- K-хроматический граф,
- Цветной граф Кэлли,
- Циклически жесткий граф,
- Циклически замкнутый граф,
- Циклически изоморфные графы,
- Циклический граф,
- Циркулянтный граф,
- Частичный граф,
- Четный граф,
- Эйлеров граф.
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.