Коды с использованием ограничителей: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KVN (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
'''Коды с использованием ограничителей''' (''[[Scheme with separators]]'') | '''Коды с использованием ограничителей''' (''[[Scheme with separators]]'') — относятся к классу ''[[линейный код|линейных кодов]]'' [[дерево|деревьев]], которые строятся в процессе [[обход графа в глубину|обхода их в глубину]] и используют в качестве характеристики [[вершина|вершин]] такие величины, как высоту, порядковый номер среди [[брат вершины v|братьев]] и др. При этом для устранения неоднозначности восстановления по таким кодам структуры деревьев применяются ограничители. Используются два варианта: | ||
1. В качестве кода берется последовательность букв <math>\alpha</math> и <math>\beta</math>, причем <math>\alpha</math> помещается в последовательность, если при обходе встречается | 1. В качестве кода берется последовательность букв <math>\alpha</math> и <math>\beta</math>, причем <math>\alpha</math> помещается в последовательность, если при обходе встречается | ||
[[внутренняя вершина]] ([[узел]]), а <math>\beta</math> | [[внутренняя вершина]] ([[узел]]), а <math>\beta</math> — если [[висячая вершина|висячая]]. Ограничитель записывается в конце каждого [[поддерево|поддерева]]. | ||
2. В качестве кода для [[бинарное дерево|бинарных деревьев]] берется последовательность чисел 0 и 1, причем левым вершинам соответствует признак "1", а правым | 2. В качестве кода для [[бинарное дерево|бинарных деревьев]] берется последовательность чисел 0 и 1, причем левым вершинам соответствует признак "1", а правым — "0"; при построении кода выписываются все [[путь|пути]] из [[корень|корня]] в [[лист|листья]], после каждого пути ставится ограничитель. | ||
[[Файл:Scheme with separators.png| | [[Файл:Scheme with separators.png|300px]] | ||
==См. также== | ==См. также== | ||
''[[Код Гапта для 2-3-деревьев]], [[Коды Ли]], [[Коды, свободные от повторений]], [[Коды с дублированием номеров вершин]], [[Линейный код]], [[Уровневые коды корневых деревьев]].'' | * ''[[Код Гапта для 2-3-деревьев]],'' | ||
* ''[[Коды Ли]],'' | |||
* ''[[Коды, свободные от повторений]],'' | |||
* ''[[Коды с дублированием номеров вершин]],'' | |||
* ''[[Линейный код]],'' | |||
* ''[[Уровневые коды корневых деревьев]].'' | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
[[Категория: Коды деревьев]] | |||
Текущая версия от 08:16, 9 октября 2019
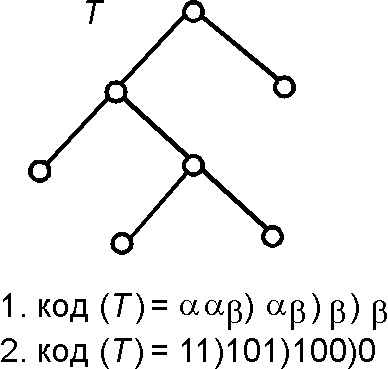
Коды с использованием ограничителей (Scheme with separators) — относятся к классу линейных кодов деревьев, которые строятся в процессе обхода их в глубину и используют в качестве характеристики вершин такие величины, как высоту, порядковый номер среди братьев и др. При этом для устранения неоднозначности восстановления по таким кодам структуры деревьев применяются ограничители. Используются два варианта:
1. В качестве кода берется последовательность букв [math]\displaystyle{ \alpha }[/math] и [math]\displaystyle{ \beta }[/math], причем [math]\displaystyle{ \alpha }[/math] помещается в последовательность, если при обходе встречается внутренняя вершина (узел), а [math]\displaystyle{ \beta }[/math] — если висячая. Ограничитель записывается в конце каждого поддерева.
2. В качестве кода для бинарных деревьев берется последовательность чисел 0 и 1, причем левым вершинам соответствует признак "1", а правым — "0"; при построении кода выписываются все пути из корня в листья, после каждого пути ставится ограничитель.
См. также
- Код Гапта для 2-3-деревьев,
- Коды Ли,
- Коды, свободные от повторений,
- Коды с дублированием номеров вершин,
- Линейный код,
- Уровневые коды корневых деревьев.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.