Коды Ли
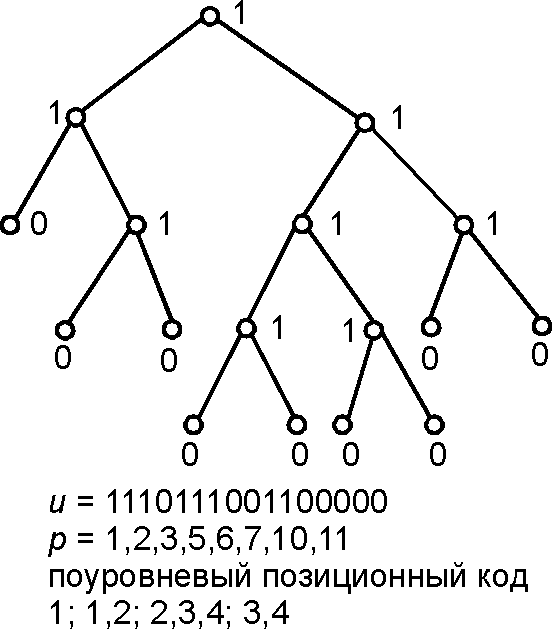
Коды Ли (Lee scheme) — относятся к классу линейных кодов деревьев. Пусть [math]\displaystyle{ \,T }[/math] — бинарное дерево, каждая внутренняя вершина помечена числом 1, а каждая висячая — числом 0. Рассматриваются следующие вариации кодов Ли:
1) [math]\displaystyle{ \,u }[/math]-кодом Ли дерева [math]\displaystyle{ \,T }[/math] называется последовательность пометок вершин, написанных в порядке обхода его в ширину;
2) [math]\displaystyle{ \,p }[/math]-кодом Ли дерева [math]\displaystyle{ \,T }[/math] называется последовательность номеров единиц в [math]\displaystyle{ u }[/math]-коде дерева [math]\displaystyle{ \,T }[/math], перечисленных в порядке их возрастания;
3) поуровневый позиционный код Ли дерева [math]\displaystyle{ \,T }[/math] высоты [math]\displaystyle{ \,h }[/math] — это последовательность [math]\displaystyle{ M=M_1,M_2,\ldots,M_{h-1} }[/math], где [math]\displaystyle{ \,M_i }[/math] — последовательность номеров внутренних вершин уровня [math]\displaystyle{ \,i }[/math], перечисленных в порядке их возрастания.
См. также
- Код Гапта для 2-3-деревьев,
- Коды, свободные от повторений,
- Коды с дублированием номеров вершин,
- Коды с использованием ограничителей,
- Линейный код,
- Уровневые коды корневых деревьев,
- Ротационный код.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.