Коды Ли: различия между версиями
Glk (обсуждение | вклад) (Создана новая страница размером '''Коды Ли''' (''Lee scheme'') - относятся к классу ''линейных кодов'' деревьев. Пусть <m...) |
KVN (обсуждение | вклад) |
||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
'''Коды Ли''' (''Lee scheme'') | '''Коды Ли''' (''[[Lee scheme]]'') — относятся к классу ''[[линейный код|линейных кодов]]'' [[дерево|деревьев]]. Пусть <math>\,T</math> — [[бинарное дерево]], каждая [[внутренняя вершина]] помечена числом 1, а каждая [[висячая вершина|висячая]] — числом 0. Рассматриваются следующие вариации кодов Ли: | ||
относятся к классу ''линейных кодов'' деревьев. Пусть <math>T</math> | |||
каждая внутренняя вершина помечена числом 1, а каждая висячая | |||
[[Файл:Lee scheme.png|350px|right]] | |||
1) <math>\,u</math>-''кодом Ли'' дерева <math>\,T</math> называется последовательность [[пометка|пометок]] [[вершина|вершин]], написанных в порядке [[обход графа в ширину|обхода его в ширину]]; | |||
2) <math>\,p</math>-''кодом Ли'' дерева <math>\,T</math> называется последовательность номеров единиц в <math>u</math>-[[код дерева|коде дерева]] <math>\,T</math>, перечисленных в порядке их возрастания; | |||
<math> | |||
См. также ''Код Гапта для 2-3-деревьев, Коды, свободные от повторений, Коды с дублированием номеров вершин, Коды с использованием ограничителей, Линейный код, Уровневые коды корневых деревьев, Ротационный код.'' | 3) ''поуровневый позиционный код Ли'' дерева <math>\,T</math> высоты <math>\,h</math> — это последовательность <math>M=M_1,M_2,\ldots,M_{h-1}</math>, где <math>\,M_i</math> — последовательность номеров внутренних вершин [[уровень вершины|уровня]] <math>\,i</math>, перечисленных в порядке их возрастания. | ||
==См. также== | |||
* ''[[Код Гапта для 2-3-деревьев]],'' | |||
* ''[[Коды, свободные от повторений]],'' | |||
* ''[[Коды с дублированием номеров вершин]],'' | |||
* ''[[Коды с использованием ограничителей]],'' | |||
* ''[[Линейный код]],'' | |||
* ''[[Уровневые коды корневых деревьев]],'' | |||
* ''[[Ротационный код]].'' | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
[[Категория: Коды деревьев]] | |||
Текущая версия от 08:12, 9 октября 2019
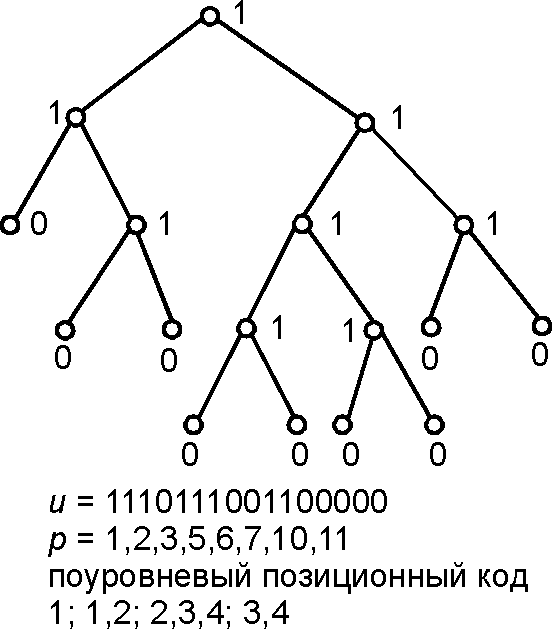
Коды Ли (Lee scheme) — относятся к классу линейных кодов деревьев. Пусть [math]\displaystyle{ \,T }[/math] — бинарное дерево, каждая внутренняя вершина помечена числом 1, а каждая висячая — числом 0. Рассматриваются следующие вариации кодов Ли:
1) [math]\displaystyle{ \,u }[/math]-кодом Ли дерева [math]\displaystyle{ \,T }[/math] называется последовательность пометок вершин, написанных в порядке обхода его в ширину;
2) [math]\displaystyle{ \,p }[/math]-кодом Ли дерева [math]\displaystyle{ \,T }[/math] называется последовательность номеров единиц в [math]\displaystyle{ u }[/math]-коде дерева [math]\displaystyle{ \,T }[/math], перечисленных в порядке их возрастания;
3) поуровневый позиционный код Ли дерева [math]\displaystyle{ \,T }[/math] высоты [math]\displaystyle{ \,h }[/math] — это последовательность [math]\displaystyle{ M=M_1,M_2,\ldots,M_{h-1} }[/math], где [math]\displaystyle{ \,M_i }[/math] — последовательность номеров внутренних вершин уровня [math]\displaystyle{ \,i }[/math], перечисленных в порядке их возрастания.
См. также
- Код Гапта для 2-3-деревьев,
- Коды, свободные от повторений,
- Коды с дублированием номеров вершин,
- Коды с использованием ограничителей,
- Линейный код,
- Уровневые коды корневых деревьев,
- Ротационный код.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.