Поиск в ширину

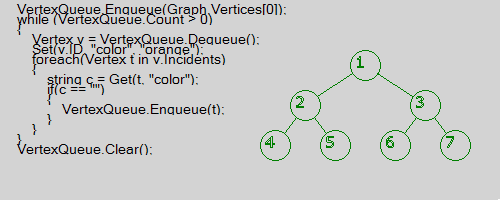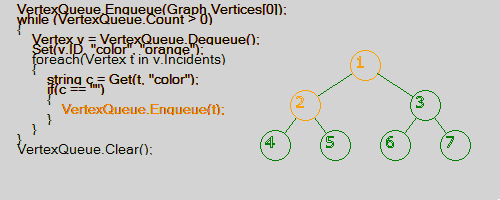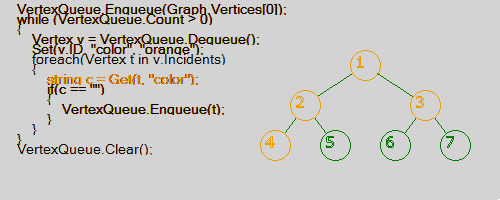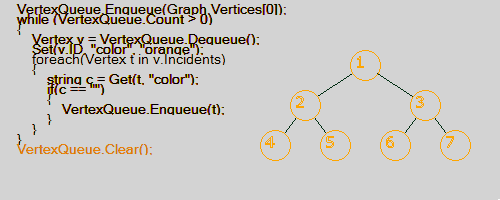
Поиск в ширину (Width (breadth) first search) — метод обхода и разметки вершин графа в следующем порядке: началу обхода [math]\displaystyle{ \,s }[/math] приписываем метку [math]\displaystyle{ \,0, }[/math] смежным с ней вершинам — метку [math]\displaystyle{ \,1. }[/math] Теперь рассматриваем поочередно окружения всех вершин с метками [math]\displaystyle{ \,1 }[/math] и каждой из входящих в эти окружения еще не занумерованных вершин приписываем метку [math]\displaystyle{ \,2 }[/math] и т.д. Если исходный граф связен, то поиск в ширину пометит все его вершины. Дуги вида [math]\displaystyle{ \,(i,i+1) }[/math] порождают остовный бесконтурный орграф, содержащий в качестве своей части остовное ордерево, называемое поисковым деревом. Легко увидеть, что с помощью поиска в ширину можно также занумеровать вершины, нумеруя вначале вершины с меткой [math]\displaystyle{ \,1, }[/math] затем с меткой [math]\displaystyle{ \,2 }[/math] и т.д.

Другое название — Обход графа в ширину.

Пример визуализации

См. также

• Обход графа,
• Топологическая сортировка,
• Укладка уграфа.

Литература

• Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.

• Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.