Деревья Гомори-Ху
Ключевые слова и синонимы
Динамические деревья (с отрезанием)
Постановка задачи
Пусть G = (V, E) – неориентированный граф, в котором |V| = n и |E| = m. Реберная связность двух вершин [math]\displaystyle{ s, t \in V \; }[/math] , обозначаемая как [math]\displaystyle{ \lambda (s, t) \; }[/math] , равняется размеру наименьшего разреза, который разделяет s и t; такой разрез называется минимальным s-t-разрезом. Очевидно, что значения [math]\displaystyle{ \lambda (s, t) \; }[/math] для всех пар вершин s и t можно представить в таблице размера [math]\displaystyle{ O(n^2) \; }[/math]. Однако из соображений эффективности лучше выбрать более сжатое представление всех значений [math]\displaystyle{ \lambda (s, t) \; }[/math]. Деревья Гомори-Ху, также известные как динамические деревья, представляют собой такое сжатое представление линейного (то есть O(n)) объема и с константным (то есть O(1)) временем просмотра. Они имеют еще одно преимущество: помимо представления всех значений [math]\displaystyle{ \lambda (s, t) \; }[/math], они также содержат структурную информацию, на основании которой для любой пары вершин s и t легко может быть получен минимальный s-t-разрез.
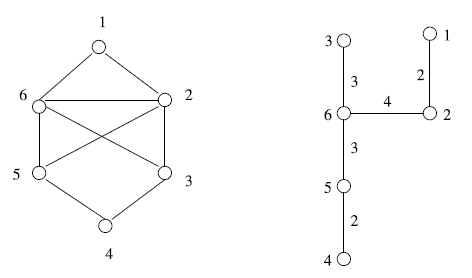
Неориентированный граф (слева) и соответствующее дерево Гомори-Ху (справа):
Формально дерево Гомори-Ху T = (V, F) для неориентированного графа G = (V, E) представляет собой взвешенное неориентированное дерево, определенное на вершинах графа, для которого выполняются следующие свойства:
• Для любой пары вершин [math]\displaystyle{ s, t \in V \; }[/math] , [math]\displaystyle{ \lambda (s, t) \; }[/math] равно минимальному весу ребра уникального пути, соединяющего s и t в T. Обозначим это ребро как e(s, t). Если на пути из s к t в T имеется несколько ребер с минимальным весом, любое из этих ребер обозначается как e(s, t).
• Для любой пары вершин s и t биразбиение вершин на компоненты, получаемые в результате удаления e(s, t) (при наличии нескольких кандидатов на e(s, t) это свойство выполняется для каждого из этих ребер) из T соответствует минимальному s-t-разрезу исходного графа G.
Для более полного понимания определения рассмотрим следующий пример: на иллюстрации представлены неориентированный граф и соответствующее дерево Гомори-Ху. Возьмем пару вершин, например, вершины 3 и 5. Очевидно, что ребро (6, 5) с весом 3 является ребром минимального веса на пути между вершинами 3 и 5 в дереве Гомори-Ху. Легко заметить, что в исходном графе [math]\displaystyle{ \lambda (s, t) = 3 \; }[/math]. Удаление этого ребра дает в результате биразбиение вершин ({1, 2, 3, 6}, {4, 5}), являющееся разрезом исходного графа размера 3.
Неочевидно, что подобные деревья Гомори-Ху существуют для всех неориентированных графов. Однако в своей классической работе 1961 года Гомори и Ху показали [7], что такие деревья не просто существуют для всех неориентированных графов, но и могут быть вычислены с использованием n – 1 операций вычисления минимальных s-t-разрезов (которые эквивалентны вычислениям максимального потока, согласно знаменитой теореме Менгера). Фактически граф может иметь несколько деревьев Гомори-Ху.
Все предыдущие алгоритмы построения деревьев Гомори-Ху в неориентированных графах использовали подпрограммы нахождения максимального потока. Гомори и Ху показали, как вычислить динамическое дерево T при помощи n – 1 операций вычисления максимального потока и операций сжатия графа. Гусфилд [8] предложил алгоритм, не использующий операций сжатия графа; все n – 1 операций вычисления максимального потока выполняются на исходном графе. Голдберг и Цюцюликлис [6] выполнили экспериментальное исследование алгоритмов, предложенных Гомори и Ху, а также Гусфилдом, для решения задачи поддержания динамического дерева, и описали эффективные реализации этих алгоритмов. Бенцур [1] привел примеры, демонстрирующие, что динамические деревья с отрезанием не существуют для ориентированных графов.
Любой подход к построению дерева Гомори-Ху, основанный на нахождении максимального потока, будет выполняться за время, в (n – 1) раз большее времени единичного вычисления максимального потока. До сих пор все более быстрые алгоритмы построения деревьев Гомори-Ху были побочными продуктами более быстрых алгоритмов нахождения максимального потока. Самый быстрый на данный момент алгоритм нахождения максимального потока с временем [math]\displaystyle{ \tilde{O} (m + n \lambda (s, t)) }[/math] (полилогарифмические сомножители n в [math]\displaystyle{ \tilde{O} }[/math]-нотации игнорируются), авторами которого были Каргер и Левайн [10], дает наилучшее ожидаемое время выполнения для алгоритма построения дерева Гомори-Ху на простых невзвешенных графах с n вершинами, равное [math]\displaystyle{ \tilde{O} (n^3) \; }[/math]. Балгат и коллеги [2] улучшили эту временную сложность до [math]\displaystyle{ \tilde{O} (mn) \; }[/math]. Заметим, что оба вышеупомянутых алгоритма являются рандомизированными алгоритмами Лас-Вегаса. Самый быстрый детерминированный алгоритм для задачи построения дерева Гомори-Ху является побочным продуктом алгоритма нахождения максимального потока Голдберга-Рао [5] и имеет время выполнения [math]\displaystyle{ \tilde{O} (nm^{1/2} min(m, n^{3/2})) }[/math].
Основные результаты
Балгат и коллеги [2] рассматривали задачу создания эффективного алгоритма построения дерева Гомори-Ху на невзвешенных неориентированных графах. Центральное место в их работе занимает теорема 1.
Теорема 1. Пусть G = (V, E) – простой невзвешенный граф, имеющий m ребер и n вершин. Тогда дерево Гомори=Ху для графа G можно построить за ожидаемое время [math]\displaystyle{ \tilde{O} (mn) }[/math]
Скорость их алгоритма всегда на коэффициент [math]\displaystyle{ \tilde{\Omega} (n^{2/9}) \; }[/math] (полилогарифмические сомножители n в [math]\displaystyle{ \tilde{\Omega} }[/math]-нотации игнорируются) выше, чем у предыдущей самой быстрой версии алгоритма.
Вместо подпрограмм нахождения максимального потока они использовали алгоритм связности по Штейнеру. Связность по Штейнеру множества вершин S (называемого множеством Штейнера) в неориентированном графе представляет собой минимальный размер разреза, разделяющего S на две части; такой разрез называется минимальным разрезом Штейнера. Обобщая алгоритм упаковки дерева, предложенный Габовым в [4], для целей нахождения реберной связности графа, Коул и Харинаран [3] предложили алгоритм нахождения связности k по Штейнеру для множества вершин в неориентированных или ориентированных невзвешенных Эйлеровых графах за время [math]\displaystyle{ \tilde{O} (mk^2) \; }[/math]. (На неориентированных графах алгоритм работает несколько быстрее – за время [math]\displaystyle{ \tilde{O}(m + nk^3) \; }[/math].) Балгат и коллеги улучшили этот результат, предложив следующую теорему.
Теорема 2. В неориентированном или ориентированном невзвешенном Эйлеровом графе связность k по Штейнеру для множества вершин может быть определена за время [math]\displaystyle{ \tilde{O} (mk) \; }[/math].
Харихаран и коллеги [9] использовали алгоритм из [3] для разработки алгоритма с ожидаемым временем выполнения [math]\displaystyle{ \tilde{O}(m + nk^3) \; }[/math] для вычисления частичного дерева Гомори-Ху для представления значений [math]\displaystyle{ \lambda (s, t) \; }[/math] для всех пар вершин s и t, удовлетворяющих условию [math]\displaystyle{ \lambda (s, t) \le k \; }[/math]. Замена алгоритма из [3] новым алгоритмом вычисления связности по Штейнеру позволяет получить частичное дерево Гомори-Ху за ожидаемое время [math]\displaystyle{ \tilde{O}(m + nk^2) \; }[/math]. Балгат и коллеги показали, что при помощи более детального анализа этот результат можно улучшить, предложив следующую теорему.
Теорема 3. Частичное дерево Гомори-Ху для невзвешенного неориентированного графа для представления всех значений [math]\displaystyle{ \lambda (s, t) \; }[/math], не превышающих k, может быть построено за ожидаемое время [math]\displaystyle{ \tilde{O} (mk) }[/math].
Поскольку [math]\displaystyle{ \lambda (s, t) \lt n \; }[/math] для всех пар вершин s и t в невзвешенном простом графе, из объявления k равным n в теореме 3 следует справедливость теоремы 1.
Применение
Деревья Гомори-Ху имеют широкое применение в обработке многотерминальных сетевых потоков и в качестве одной из важных структур данных в литературе о связности графов.
Открытые вопросы
Задача дерандомизации алгоритма, предложенного Балгатом и коллегами [2], с целью создания детерминированного алгоритма построения дерева Гомори-Ху на невзвешенных неориентированных графах с временем выполнения [math]\displaystyle{ \tilde{O} (mn) \; }[/math] остается открытой. Еще одна нерешенная задача – расширение результатов работы [2] на взвешенные графы.
Экспериментальные результаты
Голдберг и Цюцюликлис [6] выполнили широкомасштабное экспериментальное исследование алгоритмов, предложенных Гомори и Ху, а также Гусфилдом, для решения задачи поддержания динамического дерева. Они продемонстрировали варианты эффективной реализации этих алгоритмов, а также предложили и оценили эвристики для ускорения их выполнения. Согласно их наблюдениям, алгоритм Гусфилда во многих ситуациях работает быстрее, зато алгоритм Гомори и Ху более надежен. Более детальное описание результатов экспериментов можно найти в [6]. Для алгоритма, предложенного Балгатом и коллегами [2], экспериментальных результатов пока не получено. [2].
См. также
Литература
1. Benczur, A.A.: Counterexamples for Directed and Node Capacitated Cut-Trees. SIAM J. Comput. 24(3), 505-510 (1995)
2. Bhalgat, A., Hariharan, R., Kavitha, T., Panigrahi, D.: An 6(mn) Gomory-Hu tree construction algorithm for unweighted graphs. In: Proc. of the 39th Annual ACM Symposium on Theory of Computing, San Diego 2007
3. Cole, R., Hariharan, R.: A Fast Algorithm for Computing Steiner Edge Connectivity. In: Proc. of the 35th Annual ACM Symposium on Theory of Computing, San Diego 2003, pp. 167-176
4. Gabow, H.N.: A matroid approach to finding edge connectivity and packing arborescences. J. Comput. Syst. Sci. 50, 259-273 (1995)
5. Goldberg, A.V., Rao, S.: Beyond the Flow Decomposition Barrier. J. ACM 45(5), 783-797 (1998)
6. Goldberg, A.V., Tsioutsiouliklis, K.: Cut Tree Algorithms: An Experimental Study. J. Algorithms 38(1), 51-83 (2001)
7. Gomory, R.E., Hu, T.C.: Multi-terminal network flows. J. Soc. In-dust.Appl.Math. 9(4), 551-570(1961)
8. Gusfield, D.: Very Simple Methods for All Pairs Network Flow Analysis. SIAM J. Comput. 19(1), 143-155(1990)
9. Hariharan, R., Kavitha, T., Panigrahi, D.: Efficient Algorithms for Computing All Low s-t Edge Connectivities and Related Problems. In: Proc. of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms, 2007, pp. 127-136
10. Karger, D., Levine, M.: Random Sampling in Residual Graphs. In: Proc. of the 34th Annual ACM Symposium on Theory of Computing 2002, pp. 63-66