Алгоритмы обхода препятствий в беспроводных сетях датчиков
Ключевые слова и синонимы
Жадная географическая маршрутизация; дыры в маршрутах
Постановка задачи
Беспроводные сети датчиков состоят из множества небольших устройств, называемых сенсорными узлами и обладающих возможностями вычисления и радиосвязи. Сенсорные узлы обычно развертываются децентрализованным образом и используют свои датчики для сбора данных о состоянии окружающей среды. Получившаяся сеть коллективно обрабатывает, собирает и распространяет данные по исследуемой области – например, из региона, где было зарегистрировано событие, на базовую станцию или мобильному пользователю. Далее будет рассматриваться функция распространения данных по сети датчиков при наличии препятствий.
По разным причинам, включая экономию энергии и ограниченную дальность передачи сенсорных узлов, распространение информации осуществляется посредством многоскачковой передачи данных, а не односкачковой передачи на большое расстояние. Вследствие этого маршрутизация сообщений становится необходимостью. Алгоритмы маршрутизации обычно работают на сетевом уровне стека протоколов, где самым важным компонентом является (динамический) граф коммуникаций.
Определение 1 (граф коммуникаций). Беспроводная сеть датчиков рассматривается как граф G = (V, E), вершины которого соответствуют сенсорным узлам, а ребра представляют беспроводные связи между вершинами.
В беспроводных сетях датчиков действуют жесткие ограничения, из-за которых классические алгоритмы маршрутизации оказываются неэффективными, ненадежными и даже неточными. Таким образом, необходимо удовлетворять конкретные требования беспроводных сетей датчиков [2], и подход на основе географической маршрутизации позволяет разрабатывать особенно хорошо адаптированные к ним алгоритмы.
Географическая маршрутизация
Алгоритм географической маршрутизации использует преимущество знания сенсорными узлами своего местоположения, т.е. позиции в системе координат, следующей из использования протокола локализации [7]. Несмотря на значительные потенциальные накладные расходы, использование протокола локализации оказывается неизбежным во многих приложениях, в которых собираемые датчиками данные о состоянии окружающей среды будут бесполезными без привязки к определенной географической информации. В подобных приложениях имеющаяся в узлах информация об их местонахождении предполагается доступной для целей маршрутизации без дополнительных затрат.
Возможности простой географической маршрутизации
Ранние алгоритмы «пересылки наиболее продвинутому узлу в пределах диапазона» (most forward within range, MFR) или жадной географической маршрутизации [14] направляли сообщения, исходя из соображений максимизации в процессе каждого скачка продвижения по спроецированной линии на пути к точке назначения – или, напротив, минимизации оставшегося расстояния до точки назначения сообщения. Обе эти жадные эвристики объединяются под общим названием «жадная переадресация» (greedy forwarding, GF). Эта техника маршрутизации выглядит весьма многообещающей для применения в беспроводных сетях датчиков, чему есть немало причин. (1) Жадная переадресация, как это почти повсеместно требуется, является полностью децентрализованной. (2) Это облегченная техника в том смысле, что она не добавляет расходов на управление топологией. (3) Она обеспечивает коммуникацию типа «все со всеми», а не «все с одним». (4) Благодаря отсутствию предположений о структуре коммуникационного графа, который может быть ориентированным, неориентированным, стабильным или динамическим (например, вершины могут быть мобильными, а беспроводные связи могут появляться и исчезать – скажем, в силу изменений окружающей обстановки или в результате работы более низких уровней стека протоколов, таких как схемы перехода в спящий режим и выхода из него с целью экономии энергии), техника оказывается весьма надежной. (5) Она работает по запросу: до распространения сообщения не строится таблицы маршрутизации или градиента. (6) Ее эффективность связана с тем, что сообщения находят короткие пути к точкам назначения (в терминах количества скачков). (7) Техника проста и в силу этого удобна для внедрения. (8) Она эффективно использует память в том смысле, что (8а) в заголовке сообщения хранится только информация о точке назначения и (8б) процесс работает «экологично», поскольку в посещаемых сообщением сенсорных узлах не остается «мусорной» информации.
Формулировка задачи
Несмотря на все достоинства техники жадной переадресации, у нее есть серьезный недостаток: если сообщение попадает в локальный минимум, откуда невозможно успешно перейти по направлению к точке назначения, алгоритм маршрутизации прекращает работу. Локальные минимумы появляются в силу двух основных причин: дыр в маршрутах [1] и препятствий.
Определение 2. Так называемые дыры в маршрутах представляют собой области сети с малой плотностью, в которых не имеется сенсорных узлов для следующего скачка.
Даже в сетях с равномерно случайным распределением узлов дыры в маршрутах возникают в результате статистического отклонения плотности узлов. По мере снижения плотности сетей количество дыр растет, однако они серьезно влияют на эффективность GF-алгоритмов даже в сетях с очень высокой плотностью [12].
Определение 3. Препятствие, блокирующее передачу, представляет собой область сети, в которой не имеется датчиков и через которую не распространяется радиосигнал.
Очевидно, что при наличии крупных препятствий между сообщением и точкой его назначения алгоритм GF потерпит неудачу.
Задача заключается в поиске алгоритма географической маршрутизации, который сохранил бы достоинства подхода жадной переадресации, такие как простота, легкость, устойчивость и эффективность, и при этом не обладал присущим ему недостатком – невозможностью миновать узлы локального минимума, создаваемые дырами в маршрутах и крупными препятствиями, блокирующими передачу – такими как примеры на рис. 1.
Задача 1 (обход дыр в маршрутах). Первая задача заключается в выводе сообщения из множества дыр в маршрутах, статистически неизбежно возникающих даже в плотных сетях.
Задача 2 (обход препятствий по контуру). Вторая задача заключается в разработке протокола, способного направлять сообщения в обход крупных препятствий, блокирующих передачу.
Задачу 1 можно рассматривать как упрощенную версию задачи 2. Ранее были предложены облегченные решения для задачи 1, обычно использующие ограниченные функции обратной трассировки [6] или управляемого заполнения в сочетании с эвристиками жадной переадресации (GF) [4,13]. Однако, как было показано в работе [5], в которой была предложена интегрированная модель для обхода препятствий и выполнено сравнение разных алгоритмов с точки зрения их способности к такому обходу, эти решения не способны удовлетворительно справиться с задачей 2, так как они эффективно обходят только небольшие и простые препятствия.
Основные результаты
В работе [12] был предложен новый алгоритм географической маршрутизации в обход препятствий (geographic routing around obstacles, GRIC), предназначенный для решения вышеописанных задач.
Основная идея алгоритма
Стратегия подхода GF заключается в постоянной передаче сообщения соседу, обеспечивающему максимальный прогресс на пути к точке назначения. Аналогичным образом алгоритм GRIC также максимизирует прогресс в выбранном направлении. Однако это направление не всегда ориентировано на точку назначения; это идеальное направление прогресса, которое может быть вычислено согласно одной из двух возможных стратегий – режима инерции или режима восстановления, описанных ниже. Наконец, было обнаружено, что эффективность оказывается выше в присутствии слегка нестабильных сетей, как демонстрирует результат 4; поэтому в случае высокой стабильности графа коммуникаций рекомендуется использовать рандомизированную версию алгоритма GRIC, в которой вершины, собирающиеся принять решение о маршрутизации, случайным образом помечают каждую исходящую беспроводную связь как пассивную или активную. Для передачи сообщения могут использоваться только активные беспроводные связи, при этом статус связи пересматривается каждый раз, когда принимается новое решение о маршрутизации. Было обнаружено, что для практических целей хорошо подходит пометка связей активными с вероятностью p = 0,95 [12].
Режим инерции
Идея режима инерции заключается в том, что сообщение должно иметь твердое намерение двигаться к точке назначения, но это намерение должно быть смягчено для того, чтобы следовать по направлению текущего движения, «как небесное тело в планетной системе...» [12]. В режиме инерции сообщения движутся вблизи периметра дыр в маршрутах и препятствий, чтобы в конечном итоге обойти их и спланировать маршрут к точке назначения. Для реализации режима инерции необходимо сделать одно дополнительное предположение: сенсорные узлы должны знать положение узла, из которого они получают сообщение. Это может быть достигнуто, например, за счет фиксации односкачковой истории маршрутизации в заголовке сообщения. Зная свою собственную позицию p, точку назначения сообщения и предыдущее положение сообщения в одном скачке от себя, сенсорный узел может вычислить векторы [math]\displaystyle{ v_{cur} }[/math] и [math]\displaystyle{ v_{dst} }[/math], начинающиеся в позиции p и указывающие в направлении текущего движения и в направлении точки назначения сообщения, соответственно. Режим инерции определяет идеальное направление прогресса, [math]\displaystyle{ v_{idl} }[/math], как вектор, начинающийся в точке p и направленный «примерно посередине» между векторами [math]\displaystyle{ v_{cur} }[/math] и [math]\displaystyle{ v_{dst} }[/math]. Более точно, пусть [math]\displaystyle{ \alpha }[/math] – единственный угол в диапазоне [math]\displaystyle{ [ - \pi, \pi [ }[/math], такой, что [math]\displaystyle{ v_{dst} }[/math] получается в результате поворота [math]\displaystyle{ v_{cur} }[/math] на угол [math]\displaystyle{ \alpha }[/math], тогда вектор [math]\displaystyle{ v_{idl} }[/math] получается в результате поворота [math]\displaystyle{ v_{cur} }[/math] на угол [math]\displaystyle{ \alpha' }[/math], где [math]\displaystyle{ \alpha' = sign(\alpha) \cdot min \Big\{ \frac{\pi}{6}, |\alpha| \Big\} }[/math]. Наконец, сообщение жадным образом переадресуется к соседнему узлу, обеспечивающему максимальный прогресс в вычисленном идеальном направлении прогресса [math]\displaystyle{ v_{idl} }[/math].
Режим восстановления
Для повышения эффективности работы алгоритма в целом и для обхода сложных препятствий режим восстановления имитирует правило правой руки (right-hand rule, RHR) – хорошо известную технику следования вдоль стены для выхода из лабиринта. Схематичное описание RHR-компонента алгоритма GRIC приведено ниже, полное изложение можно найти в работе [12]. В контексте GRIC компонент RHR использует виртуальный компас и флаг. Виртуальный компас присваивает вектору [math]\displaystyle{ v_{cur} }[/math] значение кардинальной точки, считая точку назначения сообщения находящейся на севере. Рассматривая угол [math]\displaystyle{ \alpha }[/math], определенный выше, компас возвращает строку x-y, где x соответствует северу или югу, если [math]\displaystyle{ | \alpha | }[/math] меньше или больше [math]\displaystyle{ \pi / 2 }[/math], соответственно, а y соответствует востоку или западу, если [math]\displaystyle{ \alpha }[/math] является отрицательным или положительным, соответственно. В первый раз, когда компас возвращает значение «юг», флаг поднимается и помечается значением (x, y) компаса. Поднятие флага обозначает направление сообщения в обход препятствия по правилу RHR, если компас указывает на юго-восток. Симметричный случай, когда компас указывает на юго-запад, здесь не рассматривается; в этом случае взамен RHR будет использоваться аналогичное правило левой руки (left-hand rule, LHR). После поднятия флага он остается поднятым, а его пометка неизменной до тех пор, пока компас не укажет на север, что говорит о том, что обход препятствия завершен. Можно слегка оптимизировать процесс, опуская флаг только тогда, когда компас указывает на северо-восток (при использовании RHR), а не на северо-запад; подробнее об этом – в [12]. Согласно правилу RHR, следует двигаться в тесной близости к периметру препятствия и держаться правой стороны относительно текущего направления движения сообщения. В случае расхождения пометок компаса и флага, например, если флаг помечен значением «юго-восток», а компас выдает значение «юго-запад», считается, что сообщение слишком сильно ушло влево, рискуя уйти от препятствия и нарушить правило правой руки (симметричный подход применим к правилу левой руки). В этом случае алгоритм GRIC переходит в режим восстановления, в котором изменяется принятый по умолчанию способ вычисления [math]\displaystyle{ v_{idl} }[/math]: в режиме восстановления сообщение принудительно поворачивается направо (налево в случае применения правила LHR) путем определения [math]\displaystyle{ v_{idl} }[/math] как вектора, полученного поворотом [math]\displaystyle{ v_{cur} }[/math] на угол [math]\displaystyle{ \alpha '' }[/math] (вместо применяемого в режиме инерции [math]\displaystyle{ \alpha ' }[/math]), где [math]\displaystyle{ \alpha '' = - sign(\alpha)(2 \pi - | \alpha |)/6 }[/math].
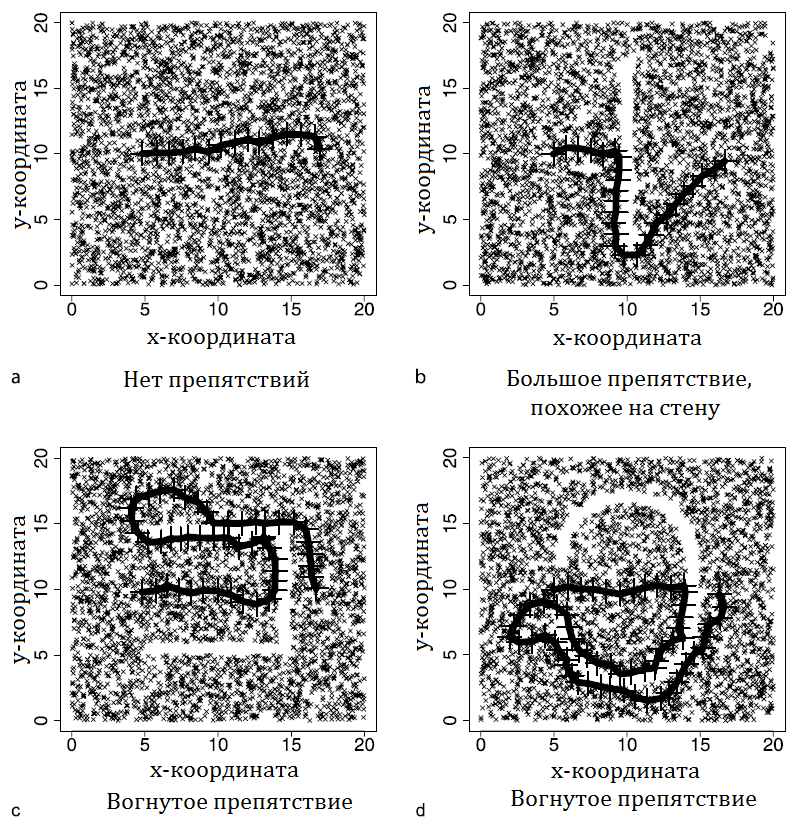
Рисунок 1. Типичный путь сообщения при использовании алгоритма GRIC для обхода определенных препятствий
Основные выводы
Эффективность алгоритма GRIC оценивалась посредством моделирования. В качестве основных параметров рассматривались присутствие (или отсутствие) крупных препятствий различной формы, блокирующих коммуникацию, и плотность сети, варьировавшаяся от очень низкой до очень высокой, от которой зависели средняя степень графа коммуникаций и наличие дыр в маршрутах. Основными метриками эффективности были степень успешности, т.е. процент сообщений, достигших точки назначения, и длина пути. Согласно результатам исследований, алгоритм GRIC эффективно, т.е. при помощи коротких путей, обходит дыры в маршрутах, но в присутствии сложных препятствий его эффективность падает со снижением плотности сети. На рис. 1 изображены типичные маршруты, найденные алгоритмом GRIC для препятствий разной формы. См. в [12] подробное описание среды моделирования.
Результат 1. В отсутствие препятствий дыры в маршрутах обходятся при любой плотности сети: процент успеха близок к 100% в случаях, когда исходная точка и точка назначения тесно связаны друг с другом. Маршрутизация является эффективной с точки зрения длины маршрутов.
Результат 2. Некоторые выпуклые препятствия, такие как на рис. 1b, обходятся с почти 100% успешностью; длины путей малы даже при невысокой плотности сети. При падении плотности до очень низкой эффективность алгоритма падает; при падении ниже критической отметки, гарантирующей связность графа коммуникаций с высокой вероятностью, имеет место быстрое падение вероятности успеха, а успешные маршруты имеют большую длину.
Результат 3. Некоторые крупные вогнутые препятствия, такие как на рис. 1c и 1d, эффективно обходятся алгоритмом. Однако при наличии подобных препятствий эффективность алгоритма становится более чувствительной к плотности сети. Процент успеха падает, а маршруты становятся длиннее при снижении плотности ниже определенного уровня, зависящего от точной формы препятствия.
Результат 4 (устойчивость). Аналогично алгоритму GF, GRIC устойчив к нестабильности связей. Более того, было отмечено, что ограниченная нестабильность связей оказывает значительное положительное влияние на эффективность работы. Это можно понять, если учесть тот факт, что сообщения с меньшей вероятностью попадают в бесконечный цикл в «горячей» системе, чем в «холодной».
Применение
Замена для жадной переадресации
Поскольку при всех преимуществах алгоритма GF он более сложен в реализации и поскольку GRIC не страдает от основных ограничений последнего, он, вероятно, может заменить GF в большинстве сценариев маршрутизации, в том числе в беспроводных сетях датчиков. В качестве примера стратегии уступающей маршрутизации [1] этот подход может быть применен скорее к GRIC, чем к GF.
Беспроводные сети датчиков с крупными препятствиями
Алгоритм GRIC успешно обходит крупные препятствия, блокирующие коммуникацию. Однако для эффективного обхода препятствий необходима достаточно высокая плотность сети. Можно сделать вывод, что функция обхода препятствий алгоритма GRIC более полезна для плотных беспроводных сетей, чем для разреженных. Беспроводные сети датчиков служат примером сетей, обычно предполагающих высокую плотность.
Динамические сети
Существуют мощные альтернативы алгоритму GRIC, такие как широко известные протоколы гарантированной доставки GFG [3], GPSR [8] и GOAFR [10]. Эти протоколы основываются на этапе планаризации, выполняемом, например, при помощи протокола обнаружения перекрестных ссылок (CLDP) [9]. LCR подразумевает значительные издержки на поддержку топологии сети, которые со временем могут быть амортизированы в случае достаточно высокой стабильности сети. Напротив, при высокой динамичности сети необходимость частых обновлений делает затраты на поддержку топологии неприемлемо высокими. Таким образом, GRIC может быть самым практичным вариантом для динамических сетей с нестабильной структурой графа коммуникаций.
Открытые вопросы
(1) Сложные вогнутые объекты, наподобие представленного на рис. 1d, по-прежнему представляют серьезную проблему для облегченных протоколов, поскольку в этой конфигурации эффективность GRIC напрямую зависит от плотности сети.
(2) Низкая и очень низкая плотность сети порождает проблемы в присутствии крупных препятствий, даже если они оказываются «простыми» и выпуклыми, как на рис. 1b.
(3) Задача, относящаяся к случаю трехмерных сетей, остается открытой. Инерция отчасти помогает делу, однако виртуальный компас и правило правой руки жестко привязаны к двумерной плоскости.
(4) GRIC не свободен от циклов. Для практических задач очень нужен механизм выявления циклов или слишком длинных маршрутов.
(5) Работа GRIC недостаточно изучена. Не имеется аналитических результатов, можно было бы также рассмотреть такие новые метрики, как срок жизни сети, потребление энергии или перегрузка по трафику.
См. также
Литература
1. Ahmed, N., Kanhere, S.S., Jha, S.: The holes problem in wireless sensor networks: a survey. SIGMOBILE Mob. Comput.Com-mun. Rev. 9,4-18 (2005)
2. Al-Karaki, J.N., Kamal, A.E.: Routing techniques in wireless sensor networks: a survey. Wirel. Commun. IEEE 11,6-28 (2004)
3. Bose, P., Morin, P., Stojmenovic, I., Urrutia, J.: Routing with guaranteed delivery in ad hoc wireless networks. In: Discrete Algorithms and Methods for Mobile Computing and Communications (1999)
4. Chatzigiannakis, I., Dimitriou, T., Nikoletseas, S., Spirakis, P.: A probabilistic forwarding protocol for efficient data propagation in sensor networks. In: European Wireless Conference on Mobility and Wireless Systems beyond 3G (EW 2004), pp. 344-350. Barcelona, Spain, 27 February 2004
5. Chatzigiannakis, I., Mylonas, G., Nikoletseas, S.: Modeling and evaluation of the effect of obstacles on the performance of wireless sensor networks. In: 39th ACM/IEEE Simulation Symposium (ANSS), Los Alamitos, CA, USA, IEEE Computer Society, pp. 50-60 (2006)
6. Chatzigiannakis, I., Nikoletseas S., Spirakis, P.: Smart dust protocols for local detection and propagation. J. Mob. Netw. (MONET) 10,621-635 (2005)
7. Karl, H., Willig, A.: Protocols and Architectures for Wireless Sensor Networks. Wiley, West Sussex (2005)
8. Karp, B., Kung, H.T.: GPSR: greedy perimeter stateless routing for wireless networks. In: Mobile Computing and Networking. ACM, New York (2000)
9. Kim, Y.J., Govindan, R., Karp, B., Shenker, S.: Lazy cross-link removal for geographic routing. In: Embedded Networked Sensor Systems. ACM, New York (2006)
10. Kuhn, F., Wattenhofer, R., Zhang, Y., Zollinger, A.: Geometric ad-hoc routing: of theory and practice. In: Principles of Distributed Computing. ACM, New York (2003)
11. Lee, S., Bhattacharjee, B., Banerjee, S.: Efficient geographic routing in multihop wireless networks. In MobiHoc '05: Proceedings of the 6th ACM international symposium on Mobile ad hoc networking and computing, pp. 230-241. ACM, New York (2005)
12. Powell, O., Nikolesteas, S.: Simple and efficient geographic routing around obstacles for wireless sensor networks. In: WEA 6th Workshop on Experimental Algorithms, Rome, Italy. Springer, Berlin (2007)
13. Stojmenovic, I., Lin, X.: Loop-free hybrid single-path/flooding routing algorithms with guaranteed delivery for wireless networks. IEEE Trans. Paral. Distrib. Syst. 12,1023-1032 (2001)
14. Takagi, H., Kleinrock, L.: Optimal transmission ranges for randomly distributed packet radio terminals. Communications, IEEE Trans. [legacy, pre - 1988]. 32,246-257 (1984)