Коды, свободные от повторений: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''Коды, свободные от повторений''' (''[[Repetition-free scheme]]'') — относятся к классу ''[[линейный код|линейных кодов]]'' [[дерево|деревьев]], которые строятся в процессе [[обход графа в глубину|обхода их в глубину]]. Используются следующие варианты: | |||
'''Коды, свободные от повторений''' (''[[Repetition-free scheme]]'') | |||
[[Файл:Repetition-free scheme.png|250px|right]] | [[Файл:Repetition-free scheme.png|250px|right]] | ||
| Строка 13: | Строка 12: | ||
==См. также== | ==См. также== | ||
''[[Код Гапта для 2-3-деревьев]], [[Коды Ли]], [[Коды с дублированием номеров вершин]], [[Коды с использованием ограничителей]], [[Линейный код]], [[Уровневые коды корневых деревьев]].'' | * ''[[Код Гапта для 2-3-деревьев]],'' | ||
* ''[[Коды Ли]],'' | |||
* ''[[Коды с дублированием номеров вершин]],'' | |||
* ''[[Коды с использованием ограничителей]],'' | |||
* ''[[Линейный код]],'' | |||
* ''[[Уровневые коды корневых деревьев]].'' | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
Версия от 10:52, 28 марта 2011
Коды, свободные от повторений (Repetition-free scheme) — относятся к классу линейных кодов деревьев, которые строятся в процессе обхода их в глубину. Используются следующие варианты:
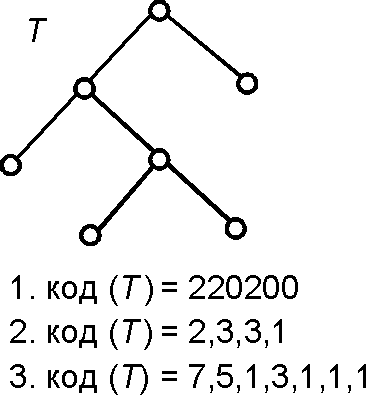
1. В качестве кода берется последовательность полустепеней исхода вершин, выписываемых в порядке, в котором вершины встречаются при обходе, с одним ограничением: при обратном движении по дереву полустепени исхода не повторяются. Бинарные деревья при таком кодировании восстанавливаются неоднозначно.
2. В качестве кода берется последовательность расстояний вершин от корня (корень не кодируется). Для деревьев, у которых полустепени исхода вершин равны 2 или 0, достаточно записывать расстояния от корня только для висячих вершин. Бинарные деревья при таком кодировании восстанавливаются неоднозначно.
3. В качестве кода берется последовательность числа вершин в поддереве с корнем в рассматриваемой в данный момент вершине.
См. также
- Код Гапта для 2-3-деревьев,
- Коды Ли,
- Коды с дублированием номеров вершин,
- Коды с использованием ограничителей,
- Линейный код,
- Уровневые коды корневых деревьев.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.