Уровневые коды корневых деревьев

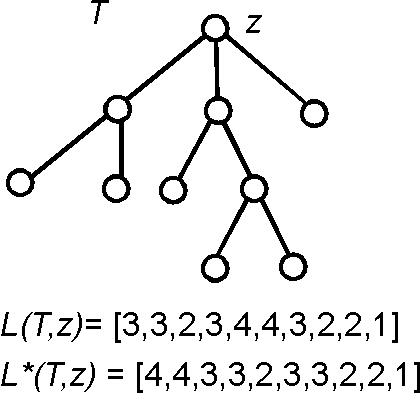
Уровневые коды корневых деревьев (Level representation of rooted trees) — Пусть [math]\displaystyle{ \,(T,z) }[/math] обозначает корневое дерево с лежащим в его основе свободным деревом [math]\displaystyle{ \,T }[/math] и корнем [math]\displaystyle{ \,z }[/math]. Уровень вершины [math]\displaystyle{ v }[/math] в [math]\displaystyle{ \,(T,z) }[/math] — это расстояние [math]\displaystyle{ \,v }[/math] от [math]\displaystyle{ \,z }[/math] плюс единица. Уровневый код (обозначение [math]\displaystyle{ L(T,z)=[l_1,l_2,\ldots,l_n] }[/math]) — это последовательность целых чисел, полученная выписыванием уровней вершин дерева [math]\displaystyle{ \,(T,z) }[/math] в постфиксном порядке. Уровневый код называется каноническим (обозначение [math]\displaystyle{ \,L^*(T,z)) }[/math], если он является наибольшим в лексикографическом упорядочении среди всех уровневых кодов, описывающих дерево.

Вершина [math]\displaystyle{ \,z }[/math] называется основным корнем свободного дерева [math]\displaystyle{ \,T }[/math] (обозначение [math]\displaystyle{ \bar{z}(T) }[/math] или просто [math]\displaystyle{ \bar{z} }[/math]), если либо [math]\displaystyle{ \,z }[/math] — единственный центр [math]\displaystyle{ \,T }[/math], либо [math]\displaystyle{ \,z }[/math] — один из центров [math]\displaystyle{ \,z_1 }[/math] и [math]\displaystyle{ \,z_2 }[/math] бицентрального дерева [math]\displaystyle{ \,T }[/math], определяемый по следующим правилам. Пусть [math]\displaystyle{ \,T_1 }[/math] и [math]\displaystyle{ \,T_2 }[/math] — поддеревья, получаемые из [math]\displaystyle{ \,T }[/math] удалением ребра, соединяющего [math]\displaystyle{ \,z_1 }[/math] и [math]\displaystyle{ \,z_2 }[/math]. В качестве [math]\displaystyle{ \,z }[/math] берется [math]\displaystyle{ \,z_1 }[/math], если либо [math]\displaystyle{ \,T_1 }[/math] имеет меньше вершин, чем [math]\displaystyle{ \,T_2 }[/math], либо [math]\displaystyle{ \,T_1 }[/math] и [math]\displaystyle{ \,T_2 }[/math] состоят из равного числа вершин, но [math]\displaystyle{ \,L^*(T_1,z_1) }[/math] лексикографически предшествует последовательности [math]\displaystyle{ \,L^*(T_2,z_2);\, z_2 }[/math] берется в противном случае. Уровневый код [math]\displaystyle{ L(T,\bar{z}) }[/math]называется главным уровневым кодом дерева [math]\displaystyle{ \,T }[/math], а [math]\displaystyle{ L^*(T,\bar{z}) }[/math] — главным каноническим уровневым кодом дерева [math]\displaystyle{ \,T }[/math].

См. также

• Код Гапта для 2-3-деревьев,
• Коды Ли,
• Коды, свободные от повторений,
• Коды с дублированием номеров вершин,
• Коды с использованием ограничителей,
• Линейный код.

Литература

• Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.