Коды с дублированием номеров вершин: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''Коды с дублированием номеров вершин''' (''[[Schemes with node number repetition]]'') | '''Коды с дублированием номеров вершин''' (''[[Schemes with node number repetition]]'') — | ||
относятся к классу ''линейных кодов'' деревьев. Используются следующие варианты: | относятся к классу ''линейных кодов'' деревьев. Используются следующие варианты: | ||
[[Файл:Schemes with node number repetition.png|420px|right]] | [[Файл:Schemes with node number repetition.png|420px|right]] | ||
1. В качестве [[код дерева|кода дерева]] берется перечень номеров [[вершина|вершин]], начиная с [[корень|корня]]; в коде дерева каждый [[узел]] встречается столько раз, сколько он проходится во время [[обход графа|обхода]], а каждая [[висячая вершина]] | 1. В качестве [[код дерева|кода дерева]] берется перечень номеров [[вершина|вершин]], начиная с [[корень|корня]]; в коде дерева каждый [[узел]] встречается столько раз, сколько он проходится во время [[обход графа|обхода]], а каждая [[висячая вершина]] — только один раз. | ||
2. В качестве кода берется перечень всех [[путь|путей]] от корня к висячим вершинам. | 2. В качестве кода берется перечень всех [[путь|путей]] от корня к висячим вершинам. | ||
| Строка 11: | Строка 11: | ||
4. В качестве кода берется перечень вершин, как в случае 3, но последовательности записываются лишь ее крайние значения. | 4. В качестве кода берется перечень вершин, как в случае 3, но последовательности записываются лишь ее крайние значения. | ||
5. В качестве кода берется 0-1-последовательность, получаемая из кода в случае 3, если вместо каждого числа в коде писать "1" при увеличении расстояния от корня на единицу и "0" | 5. В качестве кода берется 0-1-последовательность, получаемая из кода в случае 3, если вместо каждого числа в коде писать "1" при увеличении расстояния от корня на единицу и "0" — при уменьшении. Данный код является оптимальным по длине (в битах) среди всех возможных кодов [[корневое дерево|корневых]] [[упорядоченный граф|упорядоченных]] деревьев. | ||
==См. также== | ==См. также== | ||
''[[Код Гапта для 2-3-деревьев]], [[Коды Ли]], [[Код дерева]], [[Коды Закса]], [[Коды, свободные от повторений]], [[Коды с использованием ограничителей]], [[Линейный код]], [[Уровневые коды корневых деревьев]], [[Ротационный код]].'' | * ''[[Код Гапта для 2-3-деревьев]],'' | ||
* ''[[Коды Ли]],'' | |||
* ''[[Код дерева]],'' | |||
* ''[[Коды Закса]],'' | |||
* ''[[Коды, свободные от повторений]],'' | |||
* ''[[Коды с использованием ограничителей]],'' | |||
* ''[[Линейный код]],'' | |||
* ''[[Уровневые коды корневых деревьев]],'' | |||
* ''[[Ротационный код]].'' | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
Версия от 11:10, 28 марта 2011
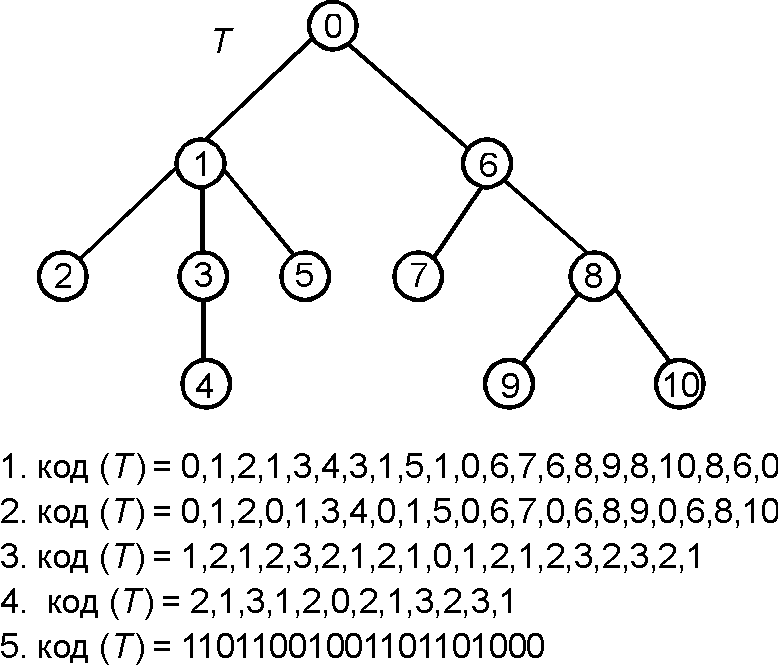
Коды с дублированием номеров вершин (Schemes with node number repetition) — относятся к классу линейных кодов деревьев. Используются следующие варианты:
1. В качестве кода дерева берется перечень номеров вершин, начиная с корня; в коде дерева каждый узел встречается столько раз, сколько он проходится во время обхода, а каждая висячая вершина — только один раз.
2. В качестве кода берется перечень всех путей от корня к висячим вершинам.
3. В качестве кода берется перечень вершин при указанном обходе, но в качестве характеристики вершины берется ее расстояние от корня.
4. В качестве кода берется перечень вершин, как в случае 3, но последовательности записываются лишь ее крайние значения.
5. В качестве кода берется 0-1-последовательность, получаемая из кода в случае 3, если вместо каждого числа в коде писать "1" при увеличении расстояния от корня на единицу и "0" — при уменьшении. Данный код является оптимальным по длине (в битах) среди всех возможных кодов корневых упорядоченных деревьев.
См. также
- Код Гапта для 2-3-деревьев,
- Коды Ли,
- Код дерева,
- Коды Закса,
- Коды, свободные от повторений,
- Коды с использованием ограничителей,
- Линейный код,
- Уровневые коды корневых деревьев,
- Ротационный код.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.