2.2 Грамматики, языки и автоматы

Next:2.3 Формулы и программы
Up:2 Словарь понятий, используемых в заданиях
Previous:2.1 Графы и системы дорог

2.2 Грамматики, языки и автоматы

Алфавитом называется конечное, непустое, упорядоченное множество символов $A=\{ a_1, \ldots, a_n \}$ .
Конечная последовательность (возможно, пустая) символов из

называется словом (или цепочкой) в алфавите

. Слова в алфавите из двух символов 0 и 1 называются двоичными.

Лексикографический порядок на словах одинаковой длины определяется следующим образом: говорят, что слово $u=a_1\ldotsa_n$ предшествует слову $v= b_1\ldots b_n$ (обозначаем ), если существует такой индекс $(0 \leq m \leq n)$ , что и для всех $(1 \leq i < m).$ Например, и

Контекстно-свободная грамматика (здесь мы будем называть ее просто грамматикой) -- это четверка , где

1) -- алфавит нетерминальных символов или нетерминалов ( нетерминалы будут обозначаться либо прописными буквами, либо курсивными словами, составленными из букв , цифр и дефиса);

2) -- алфавит терминальных символов или терминалов ( $N \cap T=\emptyset$ );
3) $S \in N$ -- начальный нетерминал;
4) -- конечное множество правил вывода, каждое из которых имеет вид $A \rightarrow v$ , где левая часть правила $A \in N$ , а правая часть -- слово в алфавите $N\cup T$ .

Как правило, мы будем рассматривать такие грамматики, в которых правые части всех правил -- непустые слова. Слово в алфавите $N\cup T$ выводимо из нетерминала , если существует его вывод из -- последовательность слов $v_0, v_1, \ldots,v_n$ такая, что , и каждое получается из $v_{i-1}$ применением некоторого правила вывода $B \rightarrow w$ из , т.е. заменой некоторого вхождения символа в $v_{i-1}$ на слово .

Слово выводимо в грамматике , если оно выводимо из ее начального нетерминала ; при этом соответствующий вывод $v_0=S, v_1, \ldots,v_n=v$ называется выводом в грамматике .

Множество всех слов в алфавите терминалов , выводимых в грамматике , называется языком грамматики и обозначается .

Две грамматики и эквивалентны, если .

Грамматика называется удлиняющей, если длины слов правых частей всех ее правил больше 1.

Пример грамматики:

$N=\{ A \}, T= \{a,b \}, S=A,P= \{ A\rightarrow aAa, A \rightarrow bAb, A \rightarrow aa, A\rightarrow bb \}$ .

Эта грамматика -- удлиняющая, ее язык -- это все симметричные слова четной ненулевой длины в алфавите $\{ a,b \}$ . Приведем вывод слова в этой грамматике:

Правило $A \rightarrow v$ мы будем записывать также в виде . При записи множеств правил с одной и той же левой частью часто используют следующее сокращения:

a) вместо $A \rightarrow v_1, A \rightarrow v_2, \ldots, A \rightarrowv_n$ пишут

$A \rightarrow \{ v_1 \mid v_2 \mid \ldots \mid v_n \}$

или

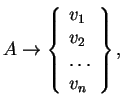
$A \rightarrow \left \{\begin{array}{l}v_1 \\ v_2 \\ \ldots \\ v_n\end{array} \right \},$

б) вместо двух правил $A \rightarrow v$ и $A \rightarrow wA$ пишут

$A \rightarrow \{w\}^* v$ .

Синтаксическим анализатором внешнего представления понятия, заданного с помощью синтаксических правил, называется такая программа, которая вводит произвольный текст и либо печатает сообщение о том, что этот текст построен в соответствии с правилами внешнего представления этого понятия (когда это действительно так), либо сообщает одну или несколько причин, из-за которых этот текст не является внешним представлением соответствующего понятия.

Автоматная диаграмма над алфавитом $X= \{ x_1,\ldots, x_n \}$ задается конечным множеством вершин (среди которых выделены начальная и конечная) и набором дуг. Из каждой вершины исходит ровно дуг, помеченных попарно различными символами из . В отличие от орграфа в диаграмме одну и ту же пару вершин могут соединять несколько дуг; могут быть и петли. Всякий путь от начальной вершины к конечной задает слово в алфавите , получающееся последовательным выписыванием пометок дуг этого пути. Множество всех таких слов обозначается и называется языком автоматной диаграммы. Автоматные диаграммы и эквивалентны, если .

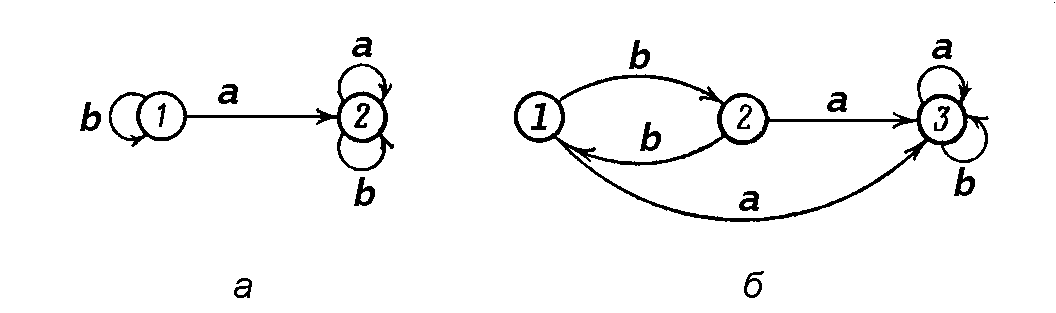
Рис. 11. Пример эквивалентных автоматных диаграмм: (а) и (б)

На рис. 11 приведен пример двух эквивалентных автоматных диаграмм. В диаграмме вершина 1 начальная, 2 конечная, в вершина 1 начальная, а 3 конечная.

Две вершины и автоматной диаграммы называются несклеиваемыми, если

а) либо одна из этих вершин конечная, а другая нет,
б) либо существует символ $x \in X$ такой, что вершины и , к которым ведут помеченные символом дуги, выходящие из вершин и соответственно, несклеиваемые.

Все остальные пары вершин автоматной диаграммы называются склеиваемыми. Например, в диаграмме на рис. 11 вершины 1 и 2 склеиваемые, остальные пары несклеиваемые.

-машиной называется вычислительное устройство, которое состоит из памяти, программы, счетчика команд и счетчика ячеек.

Память -- это последовательность из ячеек (переменных типа 0..1), занумерованных числами $1,2,\ldots,K,$ называемых адресами ячеек.

Программа -- это последовательность из команд, занумерованных числами $1,2,\ldots,M,$ называемых метками.

Счетчик команд -- это переменная типа которая хранит метку текущей команды.

Счетчик ячеек -- это переменная типа которая хранит адрес текущей ячейки.

Имеются команды следующего вида:
$:=\ L$
-- присваивает текущей ячейке значение .
$+\ L$ -- увеличивает на ,
$-\ L$ -- уменьшает на ,
$GOTO\ L$ -- устанавливает CK равным ,
$IF\ L$ -- изменяет CK на , если текущая ячейка содержит 1,
-- команда останова.

Работа -машины начинается при СК=СЯ=1и нормально завершается командой останова. При работе она реализует вычисление функции $f(\alpha)=\beta$ , где $\alpha, \beta$ -- двоичные слова длины . Аргумент $\alpha$ -- это начальное состояние памяти, он допустим, если вычисление нормально завершается. Результат $\beta$ -- это содержимое памяти в момент выполнения команды останова.
Next:2.3 Формулы и программы
Up:2 Словарь понятий, используемых в заданиях
Previous:2.1 Графы и системы дорог