
Рис. 1. Граф
Next:2.2
Грамматики, языки и автоматы
Up:2
Словарь понятий, используемых в заданиях
Previous:2
Словарь понятий, используемых в заданиях

Рис. 1. Граф ![]()
Для простоты мы будем ограничиваться классом графов без петель,
т.е. таких ребер ![]() ,
что
,
что ![]() ,
и без кратных ребер, т.е. таких, которые соединяют одну и ту же
пару вершин. Если же есть кратные ребра, то граф называется мультиграфом,
а если еще и петли, то -- псевдографом.
,
и без кратных ребер, т.е. таких, которые соединяют одну и ту же
пару вершин. Если же есть кратные ребра, то граф называется мультиграфом,
а если еще и петли, то -- псевдографом.
На рис. 1 приведен пример графа. В этом графе шесть вершин и семь ребер, степень вершин 1 - 4 равна 3, а вершин 5 - 6 равна 1.
Часть графа![]() -- это такой граф
-- это такой граф ![]() что
что ![]() и
и ![]() .
Подграфом
графа
.
Подграфом
графа ![]() называется такая его часть
называется такая его часть ![]() ,
которая вместе со всякой парой вершин
,
которая вместе со всякой парой вершин ![]() содержит и ребро
содержит и ребро ![]() ,
если оно есть в
,
если оно есть в ![]() .
Например, граф без ребер
.
Например, граф без ребер

является частью графа ![]() (рис. 1), но не его подграфом; граф
(рис. 1), но не его подграфом; граф

является подграфом графа ![]() .
.
Путь, соединяющий вершину ![]() с вершиной
с вершиной ![]() ,
-- это последовательность вершин
,
-- это последовательность вершин ![]()
![]() такая, что
такая, что ![]() и для любого
и для любого ![]()
![]() вершины
вершины ![]() и
и ![]() соединены ребром. В нем вершина
соединены ребром. В нем вершина ![]() называется начальной,
называется начальной, ![]() -- конечной, а остальные -- внутренними. Длина пути
-- конечной, а остальные -- внутренними. Длина пути![]() равна количеству ребер, т.е.
равна количеству ребер, т.е. ![]() .
Например, в графе
.
Например, в графе ![]() путь 1,3,4,2 имеет длину 3 и соединяет вершины 1 и 2.
путь 1,3,4,2 имеет длину 3 и соединяет вершины 1 и 2.
Путь ![]() называется простым, если все его вершины различны. Путь
называется простым, если все его вершины различны. Путь ![]() замкнут,
если
замкнут,
если ![]() .
Замкнутый путь, в котором все ребра различны, называется циклом. Простой
цикл -- это замкнутый путь, все вершины которого, кроме
.
Замкнутый путь, в котором все ребра различны, называется циклом. Простой
цикл -- это замкнутый путь, все вершины которого, кроме ![]() и
и ![]() ,
попарно различны.
,
попарно различны.
Гамильтоновым называется граф, в котором существует простой цикл, содержащий все вершины графа (но не обязательно все его ребра -- рис. 2).

Рис. 2. Пример гамильтонова графа ![]() .Его
простой цикл выделен полужирными линиями
.Его
простой цикл выделен полужирными линиями
Расстояние между двумя вершинами -- это длина кратчайшего пути,
соединяющего эти вершины. Например, расстояние между вершинами 3 и 4 в ![]() (рис. 2) равно 2.
(рис. 2) равно 2.
Обод -- это простой цикл -- граф, вершины которого ![]() можно занумеровать так, что для всех
можно занумеровать так, что для всех ![]()
![]() вершина
вершина ![]() соединена ребрами с
соединена ребрами с ![]() и
и ![]() ,
вершина
,
вершина ![]() -- с
-- с ![]() ,
а других ребер нет.
,
а других ребер нет.
Граф называется связным, если для любой пары вершин существует
соединяющих их путь. Максимальный связный подграф графа называется его
компонентой
связности. Вершины одной компоненты называются взаимно достижимыми.
Например, графы ![]() и
и ![]() (рис. 3) связны, а
(рис. 3) связны, а ![]() -- нет: он содержит две компоненты связности.
-- нет: он содержит две компоненты связности.
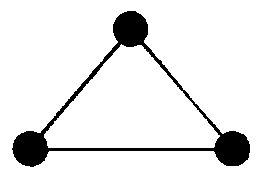
Рис. 3. Обод ![]() с минимальным числом вершин
с минимальным числом вершин
Дополнением графа ![]() называется граф
называется граф ![]() с тем множеством вершин, что и у
с тем множеством вершин, что и у ![]() ,
причем две различные вершины смежны в
,
причем две различные вершины смежны в ![]() тогда и только тогда, когда они не смежны в
тогда и только тогда, когда они не смежны в ![]() .
Граф называется полным, если любые две его различные вершины соединены
ребром. Тривиальный граф -- это граф с пустым множеством ребер,
а упорядоченный -- это граф, в котором множество преемников каждой
вершины упорядочено. Два графа
.
Граф называется полным, если любые две его различные вершины соединены
ребром. Тривиальный граф -- это граф с пустым множеством ребер,
а упорядоченный -- это граф, в котором множество преемников каждой
вершины упорядочено. Два графа ![]() и
и ![]() изоморфны,
если существует взаимно однозначное отображение (называемое
изоморфизмом)
множества вершин графа
изоморфны,
если существует взаимно однозначное отображение (называемое
изоморфизмом)
множества вершин графа ![]() на множество вершин графа
на множество вершин графа ![]() ,
сохраняющее смежность. Автоморфизмом графа
,
сохраняющее смежность. Автоморфизмом графа ![]() называется изоморфизм графа
называется изоморфизм графа ![]() на себя. Например, отображение
на себя. Например, отображение ![]() определяемое по правилам
определяемое по правилам ![]()
![]()
![]() и
и ![]() ,
является автоморфизмомом графа
,
является автоморфизмомом графа ![]() (рис. 4).
(рис. 4).

Рис. 4. Граф ![]()
Ориентированный граф, или орграф, ![]() отличается от графа тем, что
отличается от графа тем, что ![]() -- это множество упорядоченный пар
-- это множество упорядоченный пар ![]() вершин
вершин ![]() ,
называемых дугами. Дуга
,
называемых дугами. Дуга ![]() ведет от вершины
ведет от вершины ![]() к вершине
к вершине ![]() .
При этом вершину
.
При этом вершину ![]() называют преемником вершины
называют преемником вершины ![]() ,
а
,
а ![]() -- предшественником вершины
-- предшественником вершины ![]() .
Мы будем ограничиваться орграфами без петель, т.е. без дуг
.
Мы будем ограничиваться орграфами без петель, т.е. без дуг ![]() с
с ![]() (рис. 5).
(рис. 5).

Рис. 5. Орграф ![]()
Понятия части орграфа, пути, расстояния между вершинами, простого и
замкнутого пути, цикла определяются для орграфа так же, как и для графа,
но с учетом ориентации дуг. Вершина ![]() орграфа
орграфа ![]() достижима
из вершины
достижима
из вершины ![]() ,
если существует путь в
,
если существует путь в ![]() ,
ведущий от
,
ведущий от ![]() к
к ![]() .
Например, в
.
Например, в ![]() (рис. 5) все вершины достижимы из верхней.
(рис. 5) все вершины достижимы из верхней.
Деревом называется связный граф без цикла.
Корневое дерево -- это дерево с выделенной вершиной, называемой
корнем.
Все вершины корневого дерева распадаются на уровни по величине их
расстояния от корня, так, что все ребра соединяют вершины соседних уровней.
Рассматривая каждое ребро ![]() корневого дерева как дугу
корневого дерева как дугу ![]() от вершины меньшего уровня к вершине большего уровня получаем понятие ориентированного
дерева (или ордерева). Это -- связный орграф без циклов, удовлетворяющий
следующим условиям:
от вершины меньшего уровня к вершине большего уровня получаем понятие ориентированного
дерева (или ордерева). Это -- связный орграф без циклов, удовлетворяющий
следующим условиям:
а) имеется ровно одна вершина, называемая корнем, к которой не ведет ни одна дуга;
б) к каждой вершине, отличной от корня, ведет ровно одна дуга; говорят, что она соединяет отца с сыном.
В упорядоченном ордереве на множестве всех вершин, достижимых из данной
(ее потомков), задано линейное упорядочение, при котором все потомки
одного сына предшествуют всем потомкам любого более младшего. Вершины ордерева,
не имеющие сыновей, называются листьями.
Граф ![]() (рис. 4) является деревом, а орграф
(рис. 4) является деревом, а орграф ![]() (рис. 5) -- ордеревом.
(рис. 5) -- ордеревом.
Поддеревом корневого дерева ![]() называется его часть
называется его часть ![]() ,
которая является корневым деревом, удовлетворяющим следующему условию:
,
которая является корневым деревом, удовлетворяющим следующему условию: ![]() состоит из вершин и дуг, достижимых в
состоит из вершин и дуг, достижимых в ![]() от корня
от корня ![]() .
.
Двоичное (или бинарное) дерево -- это ордерево, в котором каждая вершина имеет не более двух преемников, называемых левым и правым преемниками (или сыновьями). Орграф на рис. 5 является двоичным деревом.
2-3-дерево -- это упорядоченное ордерево, в котором расстояния от корня до всех листьев совпадают, а каждая вершина, отличная от листа, имеет двух или трех преемников. На рис. 6 дан пример 2-3-дерева.

Рис. 6. Пример 2-3-дерева
Деревом (двоичного) поиска для множества чисел ![]() называется размеченное двоичное дерево, в котором каждая вершина
называется размеченное двоичное дерево, в котором каждая вершина ![]() помечена числом
помечена числом ![]() и которое удовлетворяет следующим условиям:
и которое удовлетворяет следующим условиям:
а) ![]() для всех вершин
для всех вершин ![]() ,
если вершина
,
если вершина ![]() находится в поддереве, корень которого -- левый преемник
находится в поддереве, корень которого -- левый преемник ![]() ;
;
б) ![]() для всех вершин
для всех вершин ![]() ,
если вершина
,
если вершина ![]() находится в поддереве, корень которого -- правый преемник
находится в поддереве, корень которого -- правый преемник ![]() ;
;
в) для всякого числа ![]() существует единственная вершина
существует единственная вершина ![]() ,
для которой
,
для которой ![]() .
.
Пример дерева двоичного поиска для множества чисел {5,4,8,6,1,3,9} приведен на рис. 7.

Рис. 7. Дерево двоичного поиска для целых чисел
Обозначим через ![]() максимум среди расстояний от корня дерева
максимум среди расстояний от корня дерева ![]() до его листьев (мы полагаем
до его листьев (мы полагаем ![]() ,
если
,
если ![]() пусто).
пусто).
АВЛ-деревом называется дерево двоичного поиска, в котором для
каждой вершины ![]() выполнено следующее условие:
выполнено следующее условие:
где ![]() и
и ![]() -- преемники
-- преемники ![]() ,
а
,
а ![]() и
и ![]() -- поддеревья с корнями
-- поддеревья с корнями ![]() и
и ![]() .
На рис. 8 дан пример АВЛ-дерева.
.
На рис. 8 дан пример АВЛ-дерева.
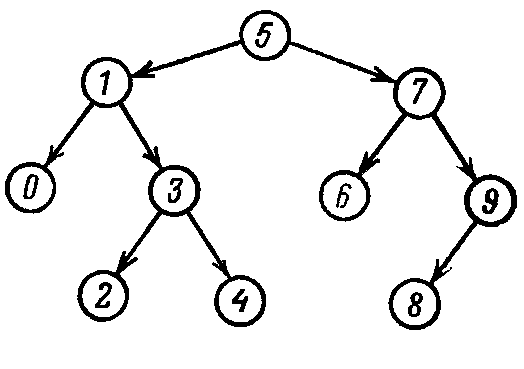
Рис. 8 АВЛ-дерево для множества чисел {5,1,7,0,3,2,4,6,9,8}
Обход корневого дерева (или ордерева)![]() состоит в посещении вершин этого дерева в некотором порядке. Например,
при его обходе в ширину вершины
состоит в посещении вершин этого дерева в некотором порядке. Например,
при его обходе в ширину вершины ![]() посещаются по уровням, начиная с корня, и слева направо (от старших потомков
к младшим). Рассмотрим три разных обхода упорядоченного дерева
посещаются по уровням, начиная с корня, и слева направо (от старших потомков
к младшим). Рассмотрим три разных обхода упорядоченного дерева ![]() (с корнем
(с корнем ![]() и его сыновьями
и его сыновьями ![]() в
глубину: префиксный, постфиксный и инфиксный обходы.
в
глубину: префиксный, постфиксный и инфиксный обходы.
Префиксный обход (прямой обход или П-обход) выполняется по следующим правилам:
1) посетить корень ![]() ;
;
2) выполнить префиксный обход поддеревьев с корнями ![]() в указанной последовательности.
в указанной последовательности.
Постфиксный обход (обратный обход или О-обход) описывается следующим образом:
1) выполнить постфиксный обход поддеревьев с корнями ![]() в указанной последовательности;
в указанной последовательности;
2) посетить корень ![]() .
.
Инфиксный обход (обход во внутреннем порядке или В-обход) определяется так:
1) выполнить инфиксный обход поддерева с корнем ![]() ;
;
2) посетить корень дерева ![]() ;
;
3) выполнить инфиксный обход поддеревьев с корнями ![]() в указанной последовательности.
в указанной последовательности.
На рис. 9 приведен порядок посещений вершин двоичного дерева при П-, О- и В-обходе.

Рис. 9. Порядок обхода вершин двоичного дерева при П-, О- и В-обходе
Система дорог -- это размеченный мультиграф (без петель), который отличается от графа тем, что в нем одна и та же пара (различных) вершин может быть связана более чем одним ребром. При этом вершины соответствуют городам, а ребра -- дорогам. Односторонним дорогам соответствуют дуги, а двусторонним дорогам -- ребра. Каждая дорога имеет некоторую длину -- положительное вещественное число.

Рис. 10. Пример системы односторонних дорог
Понятия пути, достижимости и замкнутого пути определяются для систем
дорог аналогично подобным понятиям для графов и орграфов. Длина пути
в системе дорог -- это сумма длин дорог этого пути. Расстояние между
двумя городами -- это длина минимального пути между этими городами.
Например, расстояние между городами ![]() и
и ![]() в изображенной на рис. 10 системе дорог равно 6.
в изображенной на рис. 10 системе дорог равно 6.
Next:2.2
Грамматики, языки и автоматы
Up:2
Словарь понятий, используемых в заданиях
Previous:2
Словарь понятий, используемых в заданиях