nextupprevious
Next:3 Простые программы без циклов Up:2. Простейшие программы
Previous:2.4.5 Упражнения

2.5 Задания

1. Для заданной литеры $s$ -- буквы латинского алфавита -- напечатать литеру Сдвиг$Сдвиг_N$(s) -- $N$-ю следующую за $s$ в циклическом порядке букв латинского алфавита. Например,

Сдвиг$Сдвиг_2('A') ='C'$,
Сдвиг$Сдвиг_2('Z') ='B'$,
Сдвиг$Сдвиг_{26}('A') ='A'$.

2. Имеются следующие целочисленные функции целых аргументов:

$F_0(x) = x^2 - 8x +2$,
$F_1(x) = (x - 3)*(x + x \div 2)$,
$F_2(x) = ] 100 \sin x [$,
$F_3(x) = ]\sqrt {ln(\mid x \mid + 1)}[$,
$G_0(x,y) =\mid x \mid + y,$
$G_1(x,y)= x/(1 + \mid x\mid + \mid y\mid )$,
$G_2(x,y) = 3x +4y,$
$G_3(x,y)= G_0(G_1(x,y),G_0(x,y))$,
$G_4(x,y) = G_1(G_0(x,y), G_1(x,y))$.

Для заданного целого $х$ вычислить и напечатать значение

$T_N(x) = G_{N5}(F_{N3}(F_{N4}(x)), F_{N4}(F_{N3}(x))).$

3. Имеются следующие вещественные функции вещественных аргументов:
$F_0(x) = (x^2 - 16x +8)/(1 + x^2)$,
$F_1(x) = 18 \sin x + 11 \cos x,$
$F_2(x) = \exp(x/(\mid x\mid + 5))$,
$F_3(x) = \sqrt { 3 + x^2}$,
$G_0(x,y) =\mid x + y\mid$,
$G_1(x,y) = (x - 5y)/(1 + \mid x\mid \cdot \mid y\mid)$,
$G_2(x,y) = \sin(x) + \cos(x)$,
$G_3(x,y) = \sqrt{5\cdot \mid x\mid \cdot \mid y\mid }$,
$G_4(x,y) = \ln((\mid x\mid + \mid y\mid) \cdot \mid\sin(x+y)\mid)$.

Для заданного вещественного $x$, где $-1\leq x \leq 1$, вычислить и напечатать значение
$T_N(x) = G_{N5}(F_{N3}(F_{N4}(x)),F_{N4}(F_{N3}(x) + F_{N2}(x))).$

4. Написать программу, которая находит ($N$+4)-ю степень заданного вещественного числа $х$ за минимальное количество умножений так, чтобы переменных было бы как можно меньше (среди программ с равным числом умножений).

5. На устройстве ввода задана литера $s$. Напечатать текст, получающийся конкатенацией (т.е. выписыванием друг за другом) N4+4 вхождений литеры $s$, расположенной между двумя вхождениями (N26+1)-й буквы латинского алфавита. Например, если $s$ -- это буква 'A', то программа для первого варианта (т.е. при N=1) должна печатать текст '$BАААААB$'.

6. Для заданных вещественных положительных чисел $a,b$ найти площадь четырехугольника с вершинами в точках $(-N,0),$$(0,a),$$(b,0),$$(0,-3N)$ и проверить, содержит или нет данный четырехугольник точку (1,1).

7. Логическая функция $Z_N(x,y)$ целых аргументов $x,y$ определена следующим образом:

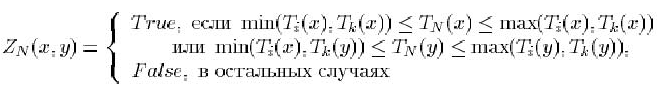
Здесь $i = \max(1,N-1)$, $k = \min(30, N+1)$, а $T_1,\ldots,T_N$ -- функции, описанные в задании 2.5.2.

Написать линейную программу (не содержащую условных операторов), которая вычисляет и печатает значение $Z_N(x,y)$ для заданных целых $x,y$.

Next:3 Простые программы без циклов Up:2. Простейшие программы
Previous:2.4.5 Упражнения

© В.Н. Касьянов, Е.В.Касьянова, 2004