Путевая ширина графа
Ключевые слова и синонимы: количество зацеплений
Постановка задачи
Путевая ширина, наряду с более известной древесной шириной, является мерой «глобальной связности» графа.
Пусть G – граф с n вершинами. Декомпозиция в форме ветвления применительно к графу G представляет собой пару [math]\displaystyle{ (T, \tau \, ) }[/math], где T – это дерево с вершинами, имеющими степень 1 или 3, а [math]\displaystyle{ \tau \, }[/math] – биекция множества листьев T на ребра G. Порядок ребра e в T, обозначаемый [math]\displaystyle{ \alpha (e)\, }[/math], представляет собой число вершин v графа G, таких, что существуют листья [math]\displaystyle{ t_1 }[/math], [math]\displaystyle{ t_2 }[/math] дерева T в различных компонентах T(V(T), E(T) — e) с [math]\displaystyle{ \tau (t_1)\, }[/math] и [math]\displaystyle{ \tau (t_2)\, }[/math], у которых v является конечной точкой.
Ширина [math]\displaystyle{ (T, \tau )\, }[/math] равна [math]\displaystyle{ max_{e \in E(T)} }[/math]{[math]\displaystyle{ \alpha (e) \, }[/math]} – иначе говоря, максимальному порядку среди всех ребер T. Путевой шириной G является минимальная ширина среди всех декомпозиций G в форме ветвления (в случае, если [math]\displaystyle{ \mid E(G)\mid \le 1 }[/math], мы устанавливаем, что путевая ширина равна 0; если [math]\displaystyle{ \mid E(G)\mid = 0 }[/math], то G не допускает декомпозиции в форме ветвления; если [math]\displaystyle{ \mid E(G)\mid = 1 }[/math], то у G имеется декомпозиция в форме ветвления, состоящая из дерева с одной вершиной – ширина этой декомпозиции считается нулевой).
Вышеприведенное определение может быть напрямую расширено на гиперграфы, в которых [math]\displaystyle{ \tau \, }[/math] представляет собой биекцию листьев T на гиперребра G. Это же определение можно так же легко распространить на матроиды.
Определение путевой ширины было введено Робертсоном и Сеймуром [25]; оно служило основным инструментом при доказательстве гипотезы Вагнера в их серии работ по минорам графов. Оно использовалось в качестве альтернативы понятию древесной ширины, поскольку оказалось более удобным для обращения в контексте этого доказательства. Отношение между путевой шириной и древесной шириной задается следующим образом.
Теорема 1 ([25])
Если G представляет собой граф, тогда [math]\displaystyle{ branchwidth(G) \le treewidth(G) + 1 \le \mathcal{b} 3/2 branchwidth(G)\mathcal{c} }[/math], где branchwidth(G) – путевая ширина графа G, а treewidth(G) – его древесная ширина.
С понятием путевой ширины связаны алгоритмические задачи двух типов: нахождение быстрых алгоритмов, вычисляющих ее значение, и использование ее для разработки быстрых алгоритмов динамического программирования для решения других задач.
Основные результаты
Алгоритмы вычисления путевой ширины
Вычисление путевой ширины представляет собой NP-полную задачу ([29]). Более того, задача является NP-полной, даже если мы ограничим ее входные графы классом расщепляемых графов или двудольных графов [20].
С другой стороны, на интервальных графах [20, 24] и круговых аркграфах [21] путевая ширина поддается вычислению за полиномиальное время. Возможно, самым популярным положительным результатом в вычислении путевой ширины является алгоритм сложности [math]\displaystyle{ O(n^2) \, }[/math] для вычисления путевой ширины планарных графов, предложенный Сеймуром и Томасом в [29]. В той же работе они приводят также алгоритм сложности [math]\displaystyle{ O(n^4) \, }[/math] для вычисления оптимальной декомпозиции в форме ветвления. (Время исполнения этого алгоритма было улучшено до [math]\displaystyle{ O(n^3) \, }[/math] в [18]). Алгоритм из [29] по существу представляет собой алгоритм для параметра, называемого разрезной шириной и связанного с маршрутизацией телефонных звонков. Значение путевой ширины планарного графа составляет половину значения разрезной ширины его медиального графа.
Алгоритм для планарных графов [29] может использоваться для построения приближенного алгоритма вычисления путевой ширины некоторых непланарных графов. На классах графов, исключающих граф с однократным пересечением в качестве минора, путевая ширина может быть аппроксимирована с коэффициентом 2.25 [7] (граф H является минором графа G, если H может быть получен из подграфа G после применения процедуры сжатия ребер). Наконец, из работы [13] следует, что для любого класса графов, замкнутых относительно операции взятия минора, может быть выполнена аппроксимация путевой ширины с постоянным коэффициентом.
Сжатие ребра или его удаление не может привести к повышению путевой ширины. Согласно теории о минорах графов, из этого следует, что для любого фиксированного k существует конечное число минимальных относительно миноров графов, путевая ширина которых превышает k; обозначим это множество графов за [math]\displaystyle{ \mathfrak{B}_k }[/math]. Проверить, содержит ли граф G фиксированный граф в качестве минора, можно за полиномиальное время [27]. Таким образом, из знания [math]\displaystyle{ \mathfrak{B}_k }[/math] следует возможность построения полиномиального по времени алгоритма для выяснения верности соотношения [math]\displaystyle{ branchwidth(G) \le k }[/math] для любого фиксированного k. К сожалению, [math]\displaystyle{ \mathfrak{B}_k }[/math] известно только для небольших значений k; в частности, [math]\displaystyle{ \mathfrak{B}_0 = \big\{ P_2 \big\} }[/math]}; [math]\displaystyle{ \mathfrak{B}_1 = \big\{ P_4 , K_3 \big\} }[/math]; [math]\displaystyle{ \mathfrak{B}_2 = \big\{ K_4 \big\} }[/math], а [math]\displaystyle{ \mathfrak{B}_3 = \big\{ K_5; V_8; M_6; Q_3 \big\} }[/math] (здесь [math]\displaystyle{ K_r \, }[/math] – это клика из r вершин; [math]\displaystyle{ P_r \, }[/math] – путь из r ребер; [math]\displaystyle{ V_8 \, }[/math] – граф, получаемый из контура с 8 вершинами, если соединить все пары вершин с расстоянием в контуре, равным 4; [math]\displaystyle{ M_6 \, }[/math] – октаэдр; а [math]\displaystyle{ Q_3 \, }[/math] – трехмерный куб). Однако для любого фиксированного k можно построить линейный относительно [math]\displaystyle{ n = |V(G)| \, }[/math] алгоритм, который определяет, выполняется ли для входного графа G соотношение [math]\displaystyle{ branchwidth(G) \le k }[/math] и, в случае положительного ответа, выдает соответствующую декомпозицию в форме ветвления [3]. Технически из этого следует, что нахождение ответа на вопрос, верно ли для конкретного графа G соотношение [math]\displaystyle{ branchwidth(G) \le k }[/math], в отношении параметра k является FPT-сложной задачей (иначе говоря, принадлежит к параметризованному классу сложности FPT). Более детальные сведения о параметризованных алгоритмах и классах сложности можно найти в [12]. Алгоритм, приведенный в статье [3], довольно сложен и использует технику характеристических последовательностей, которая также применялась для доказательства аналогичного результата в случае древесной ширины. Для конкретных случаев с [math]\displaystyle{ k \le 3 \, }[/math] существуют более простые алгоритмы, использующие технику «правило редукции» [4]. Следует понимать, что [math]\displaystyle{ \mathfrak{B}_4 }[/math] остается неизвестным, несмотря на то, что некоторые его элементы уже были обнаружены (включая графы додекаэдра и икосаэдра). Существует несколько алгоритмов, которые для заданного k могут за время [math]\displaystyle{ 2^{O(k)} \cdot n^{O(1)} }[/math] либо определить верность утверждения о том, что путевая ширина данного графа G составляет не менее k, либо построить декомпозицию в форме ветвления ширины O(k) ([26]). Эти результаты можно обобщить, чтобы вычислить путевую ширину матроидов и даже более общие параметры.
Точный алгоритм вычисления путевой ширины был приведен в [14]. Он имеет сложность [math]\displaystyle{ O((2 \cdot \sqrt{3})^n \cdot n^{O(1)}) }[/math]. Алгоритм использует особые свойства путевой ширины (см. также [24]).
В отличие от древесной ширины, максимальные по количеству ребер графы заданной путевой ширины не так легко поддаются характеризации (в случае древесной ширины они представляют собой просто k-деревья, то есть хордальные графы, все максимальные клики которых имеют размер k + 1). Алгоритм генерации таких графов, приведенный в [23], выявляет несколько структурных задач, связанных с этим параметром.
Известно, что большое число теоретико-графовых задач может быть решено за линейное время в случае, если их входные данные ограничены графами небольшой (иначе говоря, фиксированной) древесной или путевой ширины [2].
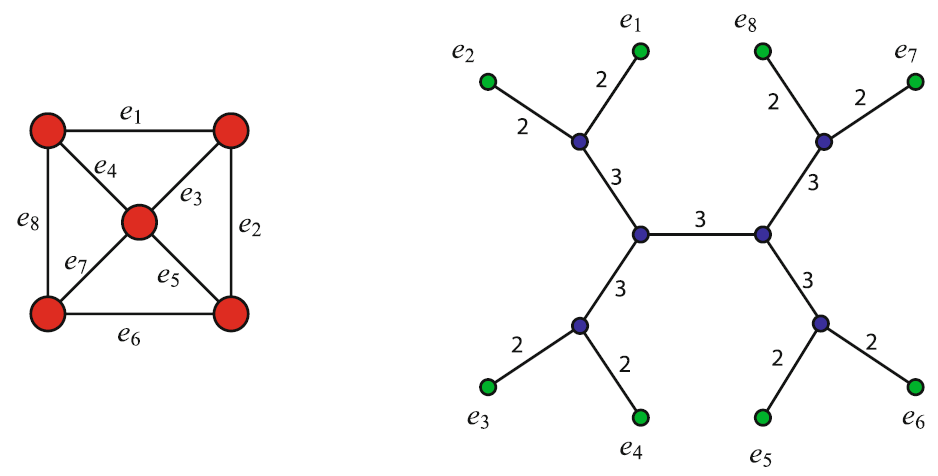
Рис. 1. Путевая ширина графа
Пример графа и его декомпозиция в форме ветвления с путевой шириной 3
Понятие путевой ширины оказалось удобным инструментом при разработке точных субэкспоненциальных алгоритмов на планарных графах и их обобщениях. Основная идея этого подхода очень проста. Пусть P – задача на графах, а [math]\displaystyle{ \mathcal{G} }[/math] – класс графов, такой, что:
для каждого графа [math]\displaystyle{ G \in \mathcal{G} }[/math] с путевой шириной, не превышающей [math]\displaystyle{ \ell \, }[/math], задача P может быть решена за время [math]\displaystyle{ 2^{c \cdot \ell} \cdot n^{O(1)} }[/math], где c является константой;
для каждого графа [math]\displaystyle{ G \in \mathcal{G} }[/math] с n вершинами декомпозиция G в форме ветвления (не обязательно оптимальная) с шириной не более h(n) может быть построена за полиномиальное время, причем h(n) является функцией.
В таком случае для каждого графа [math]\displaystyle{ G \in \mathcal{G} }[/math] задача P может быть решена за время [math]\displaystyle{ 2^{c \cdot h(n)} \cdot n^{O(1)} }[/math]. Таким образом, все сводится к вычислению констант c и функций h(n). Эти вычисления могут быть весьма сложными. В частности, как показано в [17], для каждого планарного графа G с n вершинами путевая ширина G не превышает [math]\displaystyle{ \sqrt{4.5n} \lt 2.1214 \sqrt{n} }[/math]. Расширения этой границы для графов, допускающих вложение на поверхности рода g, приведены в [15].
Дорн [9] использует подход с матричным умножением в динамическом программировании для оценки констант c для различных задач. К примеру, в задаче нахождения максимального независимого множества [math]\displaystyle{ c \le \omega/2 }[/math], где [math]\displaystyle{ \omega }[/math] < 2.376 представляет собой экспоненту матричного умножения над кольцом, из чего следует, что эта задача на планарных графах разрешима за время [math]\displaystyle{ O(2^{2.52 \sqrt{n}}) }[/math]. В задаче нахождения минимального доминирующего множества имеем [math]\displaystyle{ c \le 4 \, }[/math], что дает время работы метода декомпозиции в форме ветвления [math]\displaystyle{ O(2^{3.99 \sqrt{n}}) }[/math]. Представляется, что алгоритмы с временем исполнения [math]\displaystyle{ 2^{O( \sqrt{n})} }[/math] могут быть построены даже для некоторых «нелокальных» задач – таких как нахождение гамильтонова цикла, связного доминирующего множества и минимального дерева Штейнера, для которых нет известных алгоритмов для графов общего вида с путевой шириной [math]\displaystyle{ \ell \, }[/math], имеющих время исполнения [math]\displaystyle{ 2^{O( \ell)} \cdot n^{O(1)} }[/math] [11]. В этом случае необходимы специальные свойства некоторых оптимальных декомпозиций планарных графов в форме ветвления; грубо говоря, должно иметь место следующее: каждое ребро T соответствует диску на плоскости, такому, что все ребра G, соответствующие одному компоненту T — e, находятся внутри диска, а все остальные ребра – снаружи. Некоторые субэкспоненциальные алгоритмы на планарных графах могут быть обобщены для графов, вложенных на поверхности [10] и, далее, для классов графов, замкнутых относительно операции взятия минора [8].
Подобный же подход может использоваться для параметризованных задач на планарных графах. К примеру, параметризованный алгоритм для нахождения доминирующего множества с размером, не превышающим k (или сообщения о том, что такого множества не существует) за время [math]\displaystyle{ 2^{O( \sqrt{k} )} n^{O(1)} }[/math] может быть найден благодаря следующим наблюдениям: существует константа c, такая, что любой планарный граф, имеющий путевую ширину не менее [math]\displaystyle{ c \sqrt{k} }[/math], не содержит доминирующего множества с размером не более k. Тогда для данного k алгоритм вычисляет оптимальную декомпозицию в форме ветвления для планарного графа G, и если его ширина превышает [math]\displaystyle{ c \sqrt{k} }[/math], делает вывод, что у G не имеется доминирующего множества размера k. В ином случае оптимальное доминирующее множество вычисляется при помощи алгоритма динамического программирования за время [math]\displaystyle{ 2^{O( \sqrt{k} )} n^{O(1)} }[/math]. Имеется несколько способов ограничения параметра планарного графа в терминах его путевой или древесной ширины, включая техники, сходные с подходом Бэйкер к аппроксимационным алгоритмам [1], использование сепараторов либо некоторые комбинаторные методы, представленные в [16]. Другой обобщенный подход к ограничению путевой ширины планарного графа параметрами основан на исследованиях Робертсона и коллег [28], относящихся к быстрому исключению планарного графа, что приводит нас к понятию двумерности [6]. Параметризованные алгоритмы, основанные на декомпозиции в форме ветвления, могут быть обобщены с планарных графов на графы, вложенные в поверхности, и далее на графы, исключающие фиксированный граф в качестве минора.
Применение
В работе [5] можно ознакомиться с применением понятия путевой ширины для решения задачи коммивояжера.
Открытые вопросы
1. Известно, что любой планарный граф G имеет путевую ширину не более [math]\displaystyle{ \sqrt{4.5} \cdot \sqrt{|V(G)|} }[/math] (или не более [math]\displaystyle{ \frac{3}{2} \cdot \sqrt{|E(G)|} + 2 }[/math]) [17]. Возможно ли улучшить эту верхнюю границу? Любое возможное улучшение приведет к ускорению работы многих известных точных и параметризованных алгоритмов на планарных графах, использующих динамическое программирование или декомпозицию в форме ветвления.
2. В отличие от древесной ширины, известны очень немногие классы графов, путевая ширина которых может быть вычислена за полиномиальное время. Найти классы графов, путевая ширина которых может быть вычислена или аппроксимирована за полиномиальное время.
3. Найти [math]\displaystyle{ \mathfrak{B}_k }[/math] для значений k больше 3. Единственный структурный результат [math]\displaystyle{ \mathfrak{B}_k }[/math] заключается в том, что его планарные элементы являются либо самодвойственными, либо попарно двойственными. Это заключение следует из того факта, что двойственные планарные графы имеют одинаковую путевую ширину [29, 16].
4. Найти точный алгоритм для вычисления путевой ширины сложности [math]\displaystyle{ O*(2^n) \, }[/math] (нотация O*() предполагает, что неэкспоненциальные члены классической нотации O() отбрасываются).
5. Зависимость линейного по времени алгоритма вычисления путевой ширины от k очень велика [3]. Найти алгоритм, состоящий из [math]\displaystyle{ 2^{O(k)} \cdot n^{O(1)} }[/math] шагов, который определяет верность утверждения о том, что путевая ширина входного графа с n вершинами составляет не более k.
См. также
Литература
1. Alber, J., Bodlaender, H.L., Fernau, H., Kloks, T., Niedermeier, R.: Fixed parameter algorithms for dominating set and related problems on planar graphs. Algorithmica 33,461-493 (2002)
2. Arnborg, S.: Efficient algorithms for combinatorial problems on graphs with bounded decomposability-A survey. BIT 25,2-23 (1985)
3. Bodlaender, H.L., Thilikos, D.M.: Constructive linear time algorithms for branchwidth. In: Automata, languages and programming (Bologna, 1997). Lecture Notes in Computer Science, vol. 1256, pp. 627-637. Springer, Berlin (1997)
4. Bodlaender, H.L., Thilikos, D.M.: Graphs with branchwidth at most three. J. Algorithms 32,167-194(1999)
5. Cook, W., Seymour, P.D.: Tour merging via branch-decomposition. Inf. J. Comput. 15, 233-248 (2003)
6. Demaine, E.D., Fomin, F.V., Hajiaghayi, M., Thilikos, D.M.: Bidimensional parameters and local treewidth. SIAM J. Discret. Math. 18,501-511 (2004)
7. Demaine, E.D., Hajiaghayi, M.T., Nishimura, N., Ragde, P., Thilikos, D. M.: Approximation algorithms for classes of graphs excluding single-crossing graphs as minors. J. Comput. Syst. Sci. 69,166-195(2004)
8. Dorn, F., Fomin, F.V., Thilikos, D.M.: Subexponential algorithms for non-local problems on H-minor-free graphs. In: Proceedings of the nineteenth annual ACM-SIAM symposium on Discrete algorithms (SODA 2008). pp. 631-640. Society for Industrial and Applied Mathematics, Philadelphia (2006)
9. Dorn, F.: Dynamic programming and fast matrix multiplication. In: Proceedings of the 14th Annual European Symposium on Algorithms (ESA 2006). Lecture Notes in Computer Science, vol. 4168, pp. 280-291. Springer, Berlin (2006)
10. Dorn, F., Fomin, F.V., Thilikos, D.M.: Fast subexponential algorithm for non-local problems on graphs of bounded genus. In: Proceedings of the 10th Scandinavian Workshop on Algorithm Theory (SWAT 2006). Lecture Notes in Computer Science. Springer, Berlin (2005)
11. Dorn, F., Penninkx, E., Bodlaender, H., Fomin, F.V.: Efficient exact algorithms on planar graphs: Exploiting sphere cut branch decompositions. In: Proceedings of the 13th Annual European Symposium on Algorithms (ESA 2005). Lecture Notes in Computer Science, vol. 3669, pp. 95-106. Springer, Berlin (2005)
12. Downey, R.G., Fellows, M.R.: Parameterized complexity. In: Monographs in Computer Science. Springer, New York (1999)
13. Feige, U., Hajiaghayi, M., Lee, J.R.: Improved approximation algorithms for minimum-weight vertex separators. In: Proceedings of the 37th annual ACM Symposium on Theory of computing (STOC 2005), pp. 563-572. ACM Press, New York (2005)
14. Fomin, F.V., Mazoit, F., Todinca, I.: Computing branchwidth via efficient triangulations and blocks. In: Proceedings of the 31 st Workshop on Graph Theoretic Concepts in Computer Science (WG 2005). Lecture Notes Computer Science, vol. 3787, pp. 374-384. Springer, Berlin (2005)
15. Fomin, F.V., Thilikos, D.M.: Fast parameterized algorithms for graphs on surfaces: Linear kernel and exponential speed-up. In: Proceedings of the 31st International Colloquium on Automata, Languages and Programming (ICALP 2004). Lecture Notes Computer Science, vol. 3142, pp. 581-592. Springer, Berlin (2004)
16. Fomin, F.V., Thilikos, D.M.: Dominating sets in planar graphs: Branch-width and exponential speed-up. SIAM J. Comput. 36, 281-309(2006)
17. Fomin, F.V., Thilikos, D.M.: New upper bounds on the decomposability of planar graphs. J. Graph Theor. 51, 53-81 (2006)
18. Gu, Q.P., Tamaki, H.: Optimal branch-decomposition of planar graphs in O(n3) time. In: Proceedings of the 32nd International Colloquium on Automata, Languages and Programming (ICALP 2005). Lecture Notes Computer Science, vol. 3580, pp. 373-384. Springer, Berlin (2005)
19. Gu, Q.P., Tamaki, H.: Branch-width, parse trees, and monadic second-order logic for matroids. J. Combin. Theor. Ser. B 96, 325-351 (2006)
20. Kloks, T., Kratochvfl, J., MCiller, H.: Computing the branchwidth of interval graphs. Discret. Appl. Math. 145, 266-275 (2005)
21. Mazoit, F.:The branch-width of circular-arc graphs. In: 7th Latin American Symposium on Theoretical Informatics (LATIN 2006), 2006, pp. 727-736
22. Oum, S.I., Seymour, P.: Approximating clique-width and branch-width. J. Combin. Theor. Ser. B 96,514-528 (2006)
23. Paul, C., Proskurowski, A., Telle, J.A.: Generating graphs of bounded branchwidth. In: Proceedings of the 32nd Workshop on Graph Theoretic Concepts in Computer Science (WG 2006). Lecture Notes Computer Science, vol. 4271, pp. 205-216. Springer, Berlin (2006)
24. Paul, C., Telle, J.A.: New tools and simpler algorithms for branchwidth. In: Proceedings of the 13th Annual European Symposium on Algorithms (ESA 2005), 2005 pp. 379-390
25. Robertson, N. Seymour, P.D.: Graph minors. X. Obstructions to tree-decomposition J. Combin. Theor. Ser. B 52, 153-190 (1991)
26. Robertson, N. Seymour, P.D.: Graph minors. XII. Distance on a surface. J. Combin.Theor. Ser. B 64, 240-272 (1995)
27. Robertson, N. Seymour, P.D.: Graph minors. XIII. The disjoint paths problem. J. Combin.Theor. Ser. B 63,65-110 (1995)
28. Robertson, N., Seymour, P.D., Thomas, R.: Quickly excluding a planar graph. J. Combin. Theor. Ser. B 62, 323-348 (1994)
29. Seymour, P.D., Thomas, R.: Call routing and the ratcatcher. Combinatorica 14,217-241 (1994)