Маршрутизация в дорожных сетях с транзитными узлами: различия между версиями
Irina (обсуждение | вклад) (Новая страница: «== Ключевые слова и синонимы == Поиск кратчайших путей == Постановка задачи == Пусть дан ори…») |
(нет различий)
|
Версия от 17:06, 9 июня 2019
Ключевые слова и синонимы
Поиск кратчайших путей
Постановка задачи
Пусть дан ориентированный граф G = (V, E) с неотрицательными весами ребер. Необходимо вычислит кратчайший путь по графу G из вершины-источника s в целевую вершину t для заданных s и t. Предполагая, что граф G остается неизменными и что будет много запросов с указанием источника и цели, имеет смысл потратить некоторое время на этап предварительной обработки, который позволит очень быстро отвечать на запросы. На выходе, в зависимости от приложения, ожидается либо полное описание кратчайшего пути, либо только его длина d(s, t).
Классический алгоритм Дейкстры для решения этой задачи [ ] итеративно посещает все вершины по порядку расстояния от источника до тех пор, пока не будет достигнута целевая вершина. При обработке очень больших графов алгоритм начинает работать слишком медленно для многих приложений, из-за чего возникает необходимость в применении более специфичных техник, использующих особые свойства конкретного графа. Крайне важным на практике случаем является маршрутизация в дорожных сетях, в которых слияния и пересечения дорог трактуются как узлы, а участки дорог – как ребра, вес которых определяется некоторой весовой функцией, например, от ожидаемого времени в пути, расстояни и потребления топлива. Дорожные сети обычно являются разреженными (т. е. |E| = O(|V|)), почти планарными (т. е. в них очень небольшое число переездов) и иерархическими (т. е. можно выделить более или менее «важные» дороги). Обзор различных технологий ускорения для этой конкретной задачи приведен в работе [7].
Основные результаты
Маршрутизация в сетях с транзитными узлами [2, 3] основывается на простом наблюдении, интуитивно используемом людьми: Если вы начинаете движение из исходного узла s и движетесь куда-то «далеко», вы покинете свое текущее местоположение через одну из нескольких «важных» точек пересечений дорог, зазываемых (прямыми) узлами доступа A (s). Аналогичное рассуждение применяется и к целевому узлу, в который можно попасть только из одного из нескольких обратных узлов доступа A it). Более того, объединение всех прямых и обратных узлов доступа всех узлов, называемое множеством транзитных вершин T, весьма невелико. Из этого следуют два наблюдения, заключающиеся в том, что для каждого узла можно хранить расстояния до и из его прямых и обратных узлов доступа, а для каждой пары транзитных узлов (u, v) – расстояние между u и v. Для заданных исходного и целевого узлов s и t длина кратчайшего путь, проходящего как минимум через один транзитный узел, задается соотношением t) = minfd(s; u) + d(u; v) + d(v; t) j и € ~A(s),v 2 'Ait)}.
Заметим, что все входящие в него расстояния d(s, u), d(u, v) и d(v, t) могут быть непосредственно получены из предварительно вычисленных структур данных. Наконец, необходим также фильтр локальности 1:Ух7^ ftrue; falseg, определяющий, не находятся ли узлы s и t слишком близко друг к другу для того, чтобы перемещаться между ними через транзитный узел. Значение L должно удовлетворять свойству :L(s; t), из чего следует d(s;t) = dT(s;t). Заметим, что в общем случае обратное не обязательно должно быть справедливо, поскольку это может стать препятствием для эффективной реализации фильтра локальности.
Таким образом, могут встречаться ложноположительные значения, т. е."L(s; t) Л d(s; t) = dT(s; t)".
Следующий алгоритм может использоваться для вычисления d(s,t):
If :L(s; t), then вычислить вернуть dT(s; t); else использовать любой другой алгоритм маршрутизации.
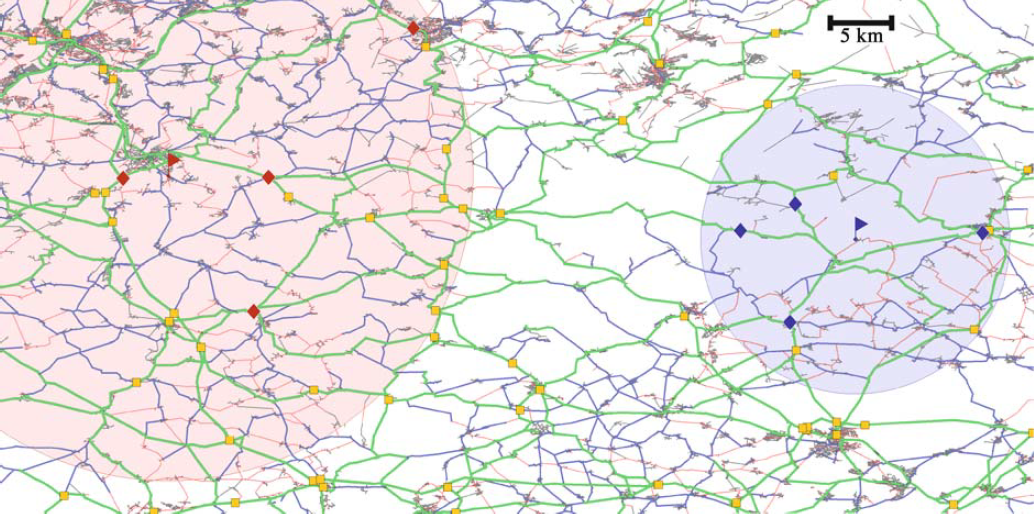
Рисунок 1. Поиск оптимального времени поездки между двумя точками (отмеченными флажками) где-то между Саарбрюккеном и Карлсруэ сводится к получению 2x4 узлов доступа (отмечены ромбами), выполнению 16 поисков по таблице между всеми парами узлов доступа и проверке, не перекрываются ли два диска, определяющие фильтр локальности. Транзитные узлы, не принадлежащие к множествам узлов доступа выбранных исходного и целевого узлов, изображены в виде маленьких квадратиков. Уровни иерархии дорог обозначены цветом: серым, красным, синим и зеленым для уровней 0-1, 2, 3 и 4, соответственно
Пример приведен на рис. 1.