Маршрутизация в дорожных сетях с транзитными узлами
Ключевые слова и синонимы
Поиск кратчайших путей
Постановка задачи
Пусть дан ориентированный граф G = (V, E) с неотрицательными весами ребер. Необходимо вычислить кратчайший путь по графу G из вершины-источника s в целевую вершину t для заданных s и t. Предполагая, что граф G остается неизменным и что будет много запросов с указанием источника и цели, имеет смысл потратить некоторое время на этап предварительной обработки, который позволит очень быстро отвечать на запросы. На выходе, в зависимости от приложения, ожидается либо полное описание кратчайшего пути, либо только его длина d(s, t).
Классический алгоритм Дейкстры для решения этой задачи [4] итеративно посещает все вершины по порядку расстояния от источника до тех пор, пока не будет достигнута целевая вершина. При обработке очень больших графов алгоритм начинает работать слишком медленно для многих приложений, из-за чего возникает необходимость в применении более специфичных техник, использующих особые свойства конкретного графа. Крайне важным на практике случаем является маршрутизация в дорожных сетях, в которых слияния и пересечения дорог трактуются как узлы, а участки дорог – как ребра, вес которых определяется некоторой весовой функцией, например, от ожидаемого времени в пути, расстояния и потребления топлива. Дорожные сети обычно являются разреженными (т. е. |E| = O(|V|)), почти планарными (т. е. в них очень небольшое число переездов) и иерархическими (т. е. можно выделить более или менее «важные» дороги). Обзор различных технологий ускорения для этой конкретной задачи приведен в работе [7].
Основные результаты
Маршрутизация при помощи транзитных узлов [2, 3] основывается на простом наблюдении, интуитивно используемом людьми: если вы начинаете движение из исходного узла s и движетесь куда-то «далеко», вы покинете свое текущее местоположение через одну из нескольких «важных» точек пересечений дорог, называемых (прямыми) узлами доступа [math]\displaystyle{ \overrightarrow{A}(s) }[/math]. Аналогичное рассуждение применяется и к целевому узлу t, в который можно попасть только из одного из нескольких обратных узлов доступа [math]\displaystyle{ \overleftarrow{A}(t) }[/math]. Более того, объединение всех прямых и обратных узлов доступа всех узлов, называемое множеством транзитных узлов [math]\displaystyle{ \mathcal{T} }[/math], весьма невелико. Из этого следуют два наблюдения, заключающиеся в том, что для каждого узла можно хранить расстояния до и из его прямых и обратных узлов доступа, а для каждой пары транзитных узлов (u, v) – расстояние между u и v. Для заданных исходного и целевого узлов s и t длина кратчайшего пути, проходящего как минимум через один транзитный узел, задается соотношением [math]\displaystyle{ d_{\mathcal{T}} (s, t) = min \{ d(s, u) + d(u, v) + d(v, t) | u \in \overrightarrow{A}(s), v \in \overleftarrow{A}(t) \} }[/math].
Заметим, что все входящие в него расстояния d(s, u), d(u, v) и d(v, t) могут быть непосредственно получены из предварительно вычисленных структур данных. Наконец, необходим также фильтр локальности [math]\displaystyle{ L: V \times V \to \{ true, false \} }[/math], определяющий, не находятся ли узлы s и t слишком близко друг к другу для того, чтобы перемещаться между ними через транзитный узел. Значение [math]\displaystyle{ L }[/math] должно удовлетворять свойству, заключающемуся в том, что из [math]\displaystyle{ \lnot{L}(s, t) }[/math] следует [math]\displaystyle{ d(s, t) = d_{\mathcal{T}}(s, t) }[/math]. Заметим, что в общем случае обратное не обязательно должно быть справедливо, поскольку это может стать препятствием для эффективной реализации фильтра локальности. Таким образом, могут встречаться ложноположительные утверждения, т. е. "[math]\displaystyle{ L(s, t) \and d(s, t) = d_{\mathcal{T}} (s, t) }[/math]".
Следующий алгоритм может использоваться для вычисления d(s, t):
Если [math]\displaystyle{ \lnot{L}(s, t) }[/math], то вычислить и вернуть [math]\displaystyle{ d_{\mathcal{T}} (s, t) }[/math]; в противном случае использовать любой другой алгоритм маршрутизации.
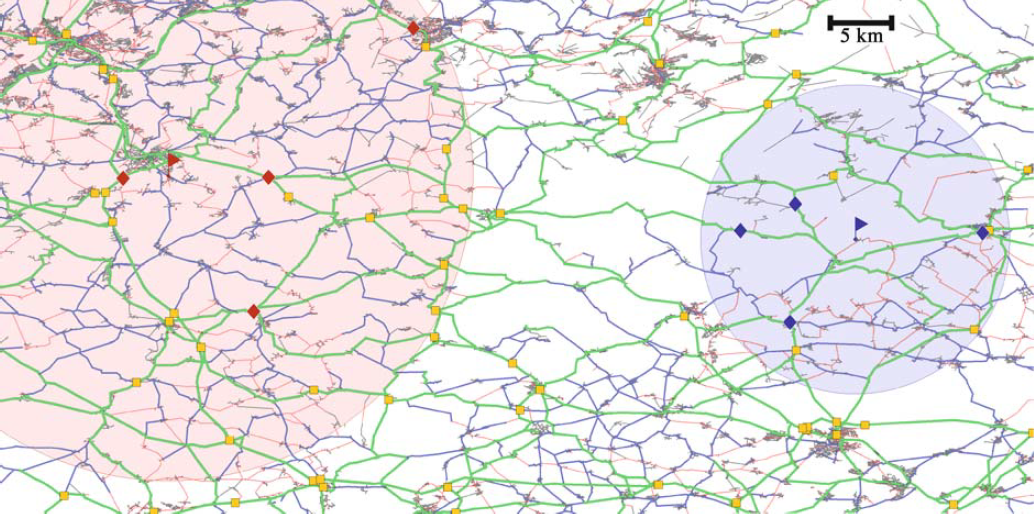
Рисунок 1. Поиск оптимального времени поездки между двумя точками (отмеченными флажками) где-то между Саарбрюккеном и Карлсруэ сводится к получению 2x4 узлов доступа (отмеченных ромбами), выполнению 16 поисков по таблице между всеми парами узлов доступа и проверке, не перекрываются ли два диска, определяющие фильтр локальности. Транзитные узлы, не принадлежащие к множествам узлов доступа выбранных исходного и целевого узлов, изображены в виде маленьких квадратиков. Уровни иерархии дорог обозначены цветом: серым, красным, синим и зеленым для уровней 0-1, 2, 3 и 4, соответственно
Пример приведен на рис. 1. Зная длину кратчайшего пути, можно эффективно вывести его полное описание при помощи итеративных поисков по таблице и заранее вычисленных представлений путей между транзитными узлами. При условии, что вышеупомянутые наблюдения справедливы, а процент ложноположительных срабатываний мал, данный алгоритм работает очень эффективно, поскольку значительная часть всех запросов может быть обработана в строке 1, [math]\displaystyle{ d_{\mathcal{T}} (s, t) }[/math] может быть вычислено при помощи нескольких поисков в таблице, а источник и цель оставшихся запросов в строке 2 оказываются достаточно близки. И в самом деле, поиск ответов на оставшиеся запросы может быть ускорен за счет введения вторичного уровня маршрутизации при помощи транзитных узлов, основанного на множестве вторичных транзитных узлов [math]\displaystyle{ {\mathcal{T}}_2 \supset {\mathcal{T}} }[/math]. В данном случае нет необходимости в вычислении и хранении полной таблицы расстояний [math]\displaystyle{ {\mathcal{T}}_2 \times {\mathcal{T}}_2 }[/math], достаточно хранить только расстояния [math]\displaystyle{ \{d(u, v) | u, v \in {\mathcal{T}}_2 \and d(u, v) \ne d_{{\mathcal{T}}}(s, t) \} }[/math], т. е. расстояния, которые не могут быть получены при помощи первичного уровня. Аналогичным образом можно добавить и более глубокие уровни.
Существуют две разных реализации, одна из которых основана на простой геометрической решетке, а другая – на иерархии дорог, самом быстром из предыдущих подходов [5, 6]. Иерархия дорог состоит из последовательности уровней (рис. 1), где уровень i + 1 строится из уровня i путем обхода узлов низкой степени и удаления ребер, которые никогда не встречаются вдали от источника или цели кратчайшего пути. Любопытно, что эти уровни постепенно геометрически уменьшаются в размере, во всех прочих отношениях они похожи друг на друга. Наивысший уровень содержит самые «важные» узлы и становится множеством первичных транзитных узлов. Узлы более низких уровней используются для формирования множеств транзитных узлов подчиненных уровней.
Применение
Помимо самого очевидного применения в автомобильных навигационных системах и серверных системах планирования маршрутов, маршрутизация при помощи транзитных узлов может применяться в нескольких других областях – например, для массового моделирования транспортных потоков и для различных задач оптимизации в логистике.
Открытые вопросы
До сих пор неизвестно, можно ли найти более эффективные множества транзитных узлов или лучший фильтр локальности для дальнейшего улучшения производительности. Неясно также, может ли маршрутизация при помощи транзитных узлов успешно применяться к другим типам графов, отличным от дорожных сетей. В этом контексте было бы желательно получить какие-либо теоретические гарантии, применимые к любому графу, обладающему определенными свойствами. Для некоторых практических областей применения пригодилась бы динамическая версия маршрутизации при помощи транзитных узлов для работы с сетями, зависящими от времени, или непредсказуемыми изменениями весов дуг, вызванными, к примеру, заторами на дорогах. Последний сценарий может обрабатываться с помощью родственного подхода из работы [8], однако он работает гораздо медленнее, чем маршрутизация при помощи транзитных узлов.
Экспериментальные результаты
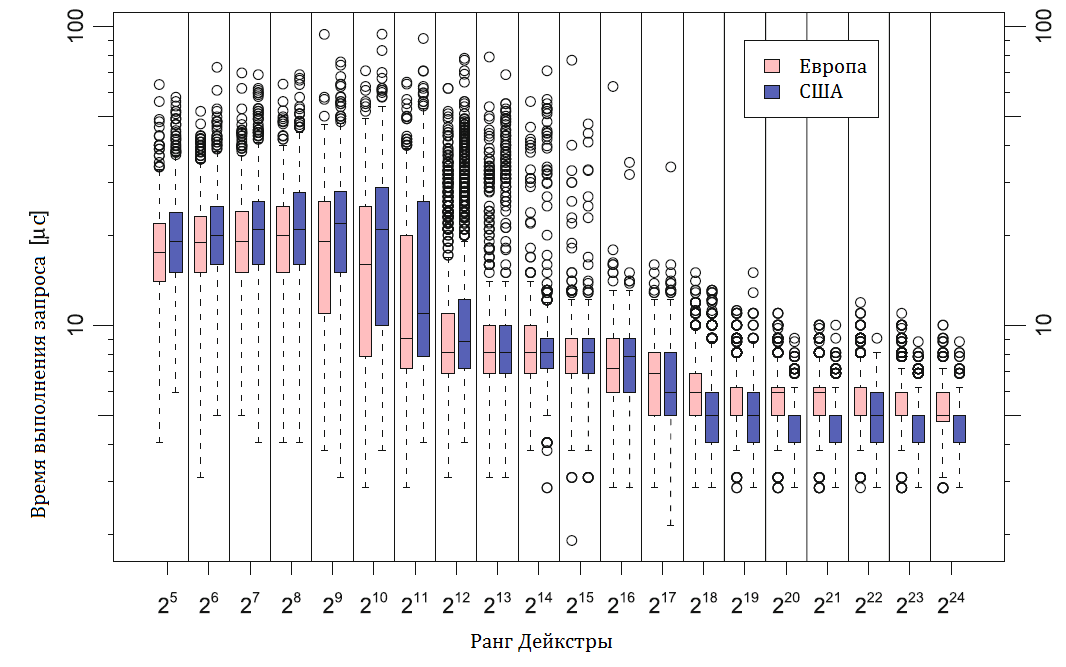
Эксперименты проводились на дорожных сетях Западной Европы и США с использованием целевой функции, учитывающей только ожидаемое время в пути. Результаты отражают различные компромиссы между средним временем выполнения запроса (от 5 до 63 микросекунд для США), продолжительностью предварительной обработки (от 59 до 1200 минут) и затратами на хранение (от 21 до 244 байт на узел). Для варианта, использующего три уровня и настроенного для минимального времени выполнения запроса, в таблицах 1 и 2 показана статистика для продолжительности предварительной обработки и эффективности запросов, соответственно. Среднее время выполнения запроса, около 5 микросекунд, на шесть порядков величины меньше, чем у алгоритма Дейкстры. На рис. 2 для каждого ранга r на оси x приведено распределение для 1000 запросов со случайной исходной точкой s и целевым узлом t, для нахождения ответа на которые алгоритму Дейкстры требуется r итераций. Можно различить три уровня маршрутизации при помощи транзитных узлов с небольшими зонами перехода между ними: для больших рангов достаточно обращения только к первичному уровню, что дает время выполнения запроса около 5 микросекунд, для меньших рангов требуются дополнительные уровни и медианное время выполнения запроса возрастает до 20 микросекунд.
| уровень 1 | уровень 2 | уровень 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ | \mathcal{T} | }[/math] | [math]\displaystyle{ |A| }[/math] ср. | [math]\displaystyle{ | \mathcal{T}_2 | }[/math] | [math]\displaystyle{ | table_2 | [ \times 10^6 ] }[/math] | [math]\displaystyle{ |A_2| }[/math] ср. | [math]\displaystyle{ | \mathcal{T}_3 | }[/math] | [math]\displaystyle{ | table_3 | [ \times 10^6 ] }[/math] | память [байт/узел] | время [ч] | |
| Европа | 11 293 | 9,9 | 323 356 | 130 | 4,1 | 2 954 721 | 119 | 251 | 2:44 |
| США | 10 674 | 5,7 | 485 410 | 204 | 4,2 | 3 855 407 | 173 | 244 | 3:25 |
Таблица 1. Статистика по предварительной обработке. Представлены мощность множеств транзитных узлов, число записей в таблицах расстояний и среднее число узлов доступа на соответствующем уровне, а также расход памяти и время предварительной обработки
| к-во узлов | к-во ребер | уровень 1 | уровень 2 | уровень 3 | запрос | |
|---|---|---|---|---|---|---|
| Европа | 18 029 721 | 42 199 587 | 99,74% | 99,9984% | 99,99981% | 5,6 [math]\displaystyle{ \mu c }[/math] |
| США | 24 278 285 | 58 213 192 | 99,89% | 99,9986% | 99,99986% | 4,9 [math]\displaystyle{ \mu c }[/math] |
Таблица 2. Эффективность алгоритма маршрутизации при помощи транзитных узлов на 10 000 000 случайных запросов. Столбец для уровня i показывает, на какую часть запросов был дан точный ответ с использованием только информации, доступной на уровнях не выше i. Каждый «ящик» простирается от нижнего до верхнего квартиля и содержит медианное значение, «усы» простираются до минимального и максимального значений, исключая выбросы, изображенные отдельно
Рисунок 2. Распределение времени ответа на запросы как функция от ранга Дейкстры – количества итераций, которое требуется алгоритму Дейкстры для решения данного экземпляра задачи. Распределения представлены в виде «ящика с усами»: каждый «ящик» простирается от нижнего до верхнего квартиля и содержит медианное значение, «усы» простираются до минимального и максимального значений, исключая выбросы, изображенные отдельно
Наборы данных
Карта дорожной сети Европы была предоставлена компанией PTV AG, карта сети США была получена из файлов TIGER/Line [9]. Оба графа также использовались в ходе 9-го конкурса DIMACS по реализации алгоритмов поиска кратчайших путей [1].
Ссылка на код
Исходный код будет в свое время опубликован на сайте http://algo2.iti.uka.de/schultes/hwy/.
См. также
- Алгоритм поиска кратчайших путей в разреженных графах
- Алгоритм поиска кратчайших путей при помощи матричного произведения
- Декрементный алгоритм нахождения кратчайших путей между всеми парами
- Разработка алгоритмов для применения в больших сетях
- Полностью динамический алгоритм нахождения кратчайших путей между всеми парами
- Географическая маршрутизация
- Конкурс по реализации алгоритмов поиска кратчайших путей
- Подход к составлению расписания при помощи кратчайших путей
- Поиск кратчайших путей в планарных графах с отрицательными весами ребер
- Алгоритм поиска кратчайших путей с единственным источником
Литература
1. 9th DIMACS Implementation Challenge: Shortest Paths. http://www.dis.uniroma1.it/~challenge9/(2006)
2. Bast, H., Funke, S., Matijevic, D., Sanders, P., Schultes, D.: In transit to constant time shortest-path queries in road networks. In: Workshop on Algorithm Engineering and Experiments, 2007, pp. 46-59
3. Bast, H., Funke, S., Sanders, P., Schultes, D.: Fast routing in road networks with transit nodes. Science 316(5824), 566 (2007)
4. Dijkstra, E.W.: A note on two problems in connexion with graphs. Numer. Math. 1 269-271 (1959)
5. Sanders, P., Schultes, D.: Highway hierarchies hasten exact shortest path queries. In: 13th European Symposium on Algorithms. LNCS, vol. 3669, pp. 568-579. Springer, Berlin (2005)
6. Sanders, P., Schultes, D.: Engineering highway hierarchies. In: 14th European Symposium on Algorithms. LNCS, vol. 4168, pp. 804-816. Springer, Berlin (2006)
7. Sanders, P., Schultes, D.: Engineering fast route planning algorithms. In: 6th Workshop on Experimental Algorithms. LNCS, vol. 4525, pp. 23-36. Springer, Berlin (2007)
8. Schultes, D., Sanders, P.: Dynamic highway-node routing. In: 6th Workshop on Experimental Algorithms. LNCS, vol. 4525, pp. 66-79. Springer, Berlin (2007)
9. U.S. Census Bureau, Washington, DC: UA Census 2000 TIGER/Line Files. http://www.census.gov/geo/www/tiger/tigerua/ua_tgr2k.html (2002)