Миграция данных

Ключевые слова и синонимы

Перенос файлов; перемещение данных

Постановка задачи

Задача обусловлена необходимостью управления данными, хранящимися на множестве устройств, для обработки динамически меняющихся потребностей. Чтобы обеспечить максимально эффективное использование данных, их расположение (т.е. отображение, определяющее местонахождение подмножеств элементов данных на каждом диске) необходимо вычислять с учетом емкостей дисков и потребностей в данных. По мере изменения потребности в данных со временем системе необходимо создавать новое расположение. Задача миграции данных заключается в вычислении эффективного графика для множества дисков, позволяющего преобразовать исходное расположение в целевое.

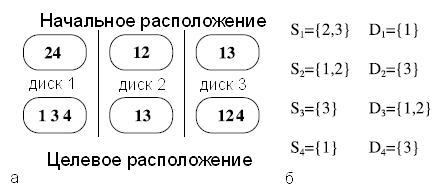
Рисунок 1. Слева: примеры исходного и целевого расположения данных. Справа: соответствующие множества $S_i$ и $D_i$

Определение задачи выглядит следующим образом. Предположим, что имеется N дисков и $\mathrm{\Delta }$ элементов данных и что заданы исходное и целевое расположения (см. пример на рис. 1а). Для каждого элемента i его диски-источники $S_i$ определяются как подмножество дисков, содержащих элемент i в своем исходном расположении. Диски-назначения $D_i$ представляют собой подмножество дисков, желающих получить элемент i. Иными словами, диски из $D_i$ должны хранить элемент i в целевом расположении, но не в исходном. На рис. 1б представлены соответствующие множества $S_i$ и $D_i$. Предполагается, что $S_i\ne \mathrm{\varnothing }$ и $D_i\ne \mathrm{\varnothing }$ для каждого элемента i. Миграция данных представляет собой перенос данных таким образом, чтобы все множества $D_i$ получили элемент i, изначально находившийся в $S_i$, а задача заключается в минимизации общего времени, необходимого для переносов.

Предположим, что в основе системы лежит полностью связная сеть, а все элементы данных имеют один и тот же размер. Иными словами, перемещение элемента данных с одного диска на другой всегда занимает одно и то же время.

Следовательно, миграция осуществляется в несколько раундов. Рассмотрим полудуплексную модель, в которой каждый диск может участвовать в передаче только одного элемента данных – в качестве отправителя либо получателя. Задача заключается в построении графика миграции с минимальным количеством раундов. Использование обходных вершин не допускается (то есть вершин, не являющихся целью операции перемещения, но используемых как промежуточные точки хранения элемента данных), так что все элементы данных направляются только дискам, которым они требуются.

Основные результаты

Хуллер и др. [11] разработали 9,5-аппроксимацию для задачи миграции данных, коэффициент которой был впоследствии улучшен до 6.5 + o(1). Далее мы рассмотрим нижние границы задачи.

Нотация и нижние границы

1. Максимальная полустепень захода ( $\beta$): Пусть ${\beta }_j$ – количество элементов данных, которые собирается получить диск j. Иными словами, ${\beta }_j=|\{i|j\in D_i\}|$. Тогда $\beta =ma{x}_j{\beta }_j$ является нижней границей оптимума, поскольку диск может получить только один элемент данных в одном раунде.

2. Максимальное количество элементов, источником или назначением которых может быть диск $(\alpha$): Для каждого элемента i по меньшей мере один диск в $S_i$ должен быть использован в качестве источника элемента, этот диск называется первичным источником. Уникальный первичный источник $s_i\in S_i$ для каждого элемента i, минимизирующего значение $\alpha =ma{x}_{j=1,...,N}(|\{i|j=s_i\}|)$, может быть найден при помощи алгоритма вычисления потока в сети. Отметим, что $\alpha \ge \beta$; $\alpha$ также является нижней границей оптимального решения.

3. Минимальное время, необходимое для клонирования (M): Пусть диск j делает копию элемента i в k-м раунде. В конце m-го раунда количество копий, которые могут быть созданы из этой копии, не превышает $2^{m-k}$, поскольку в каждом раунде количество копий может только удваиваться. Отметим также, что каждый диск может в одном раунде сделать копию только одного элемента. Поскольку нужно создать не менее $|D_i|$ копий элемента i, минимальное значение m, удовлетворяющее следующей линейной программе, задает нижнюю границу оптимального решения:

L(m):

Алгоритм миграции данных

9,5-аппроксимацию можно получить следующим образом.

Алгоритм вначале вычисляет множества представителей для каждого элемента и отправляет элемент в множество, которое, в свою очередь, пересылает элемент в оставшееся множество. Множества представителей вычисляются по-разному в зависимости от размера $D_i$.

Представители для больших множеств

Для множеств размером не менее $\beta$ непересекающаяся коллекция множеств представителей $R_i,i=l,...,\mathrm{\Delta }$ должна удовлетворять следующим свойствам: (1) каждое множество $R_i$ должно быть подмножеством $D_i$, (2) $|R_i|=\lfloor |D_i|/\beta \rfloor$. Множества представителей могут быть найдены при помощи алгоритма вычисления потока в сети.

Представители для маленьких множеств

Для каждого элемента i положим ${\gamma }_i=|D_i|modk$. Необходимо вычислить вторичного представителя $r_iвD_i$ для элементов с ${\gamma }_i\ne 0$. Диск j может быть вторичным представителем $r_i$ для нескольких элементов, если $\sum _{i\in I_j}{\gamma }_i\le 2\beta +1$, где $I_j$ – множество элементов, для которых j является вторичным представителем. Это можно сделать при помощи алгоритма Шмойса-Тардош [17] для обобщенной задачи о назначениях.

Планирование миграций

Если имеются представители для всех элементов данных, миграцию можно выполнить в три этапа следующим образом:

1. Миграция в $R_i$: каждый элемент данных вначале отправляется в множество $R_i$. Преобразуя дробное решение, приведенное в L(M), можно найти график миграции из $s_i$ в $R_i$, требующий не более $2M+\alpha$ раундов.

2. Миграция в $r_i$: элемент i отправляется из первичного источника $s_i$ в $r_i$. Эту миграцию можно выполнить за $1,5\alpha$ раундов при помощи раскраски ребер [16].

3. Миграция на оставшиеся диски: Теперь можно создать граф переноса из представителей на оставшиеся диски следующим образом. Для каждого элемента i добавьте ориентированные ребра от дисков в Ri к ф - 1) |_^J дискам в D \ Rt, такие, что полустепень выхода каждой вершины в Ri не превышает f$ — 1, а полустепень входа каждой вершины в Д \ Ri из Ri равна 1. Также добавляется ориентированное ребро от вторичного представителя ri элемента i к оставшимся дискам в D, не имеющим входящих ребер из Ri. Было показано, что максимальная степень графа переносов не превышает 4/3 – 5, а кратность равна f$ + 2. Следовательно, миграцию из графа переносов можно выполнить за 5f$ - 3 раундов при помощи алгоритма раскраски ребер мультиграфа [18].

Анализ

Заметим, что общее количество раундов, необходимых для выполнения вышеописанного алгоритма, не превышает 2M + 2.5a + 5f$ - 3. Поскольку a, f$ и M являются нижними границами оптимального количества раундов, этот алгоритм дает 9,5-аппроксимацию.

Теорема 1 ([11]). Существует алгоритм 9,5-аппроксимации для задачи миграции данных. Хуллер и др. [10] позднее улучшили его, получив (6,5 + o(1))-аппроксимацию.

Теорема 2 ([10]). Существует алгоритм (6.5 + o(1))-аппроксимации для задачи миграции данных.

Применение

Миграция данных в системах хранения