Миграция данных

Ключевые слова и синонимы

Перенос файлов; перемещение данных

Постановка задачи

Задача обусловлена необходимостью управления данными, хранящимися на множестве устройств, для обработки динамически меняющихся потребностей. Чтобы обеспечить максимально эффективное использование данных, их расположение (т.е. отображение, определяющее местонахождение подмножеств элементов данных на каждом диске) необходимо вычислять с учетом емкостей дисков и потребностей в данных. По мере изменения потребности в данных со временем системе необходимо создавать новое расположение. Задача миграции данных заключается в вычислении эффективного графика для множества дисков, позволяющего преобразовать исходное расположение в целевое.

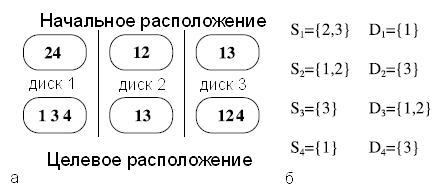
Рисунок 1. Слева: примеры исходного и целевого расположения данных. Справа: соответствующие множества [math]\displaystyle{ S_i \; }[/math] и [math]\displaystyle{ D_i \; }[/math]

Определение задачи выглядит следующим образом. Предположим, что имеется N дисков и [math]\displaystyle{ \Delta \; }[/math] элементов данных и что заданы исходное и целевое расположения (см. пример на рис. 1а). Для каждого элемента i его диски-источники [math]\displaystyle{ S_i \; }[/math] определяются как подмножество дисков, содержащих элемент i в своем исходном расположении. Диски-назначения [math]\displaystyle{ D_i \; }[/math] представляют собой подмножество дисков, желающих получить элемент i. Иными словами, диски из [math]\displaystyle{ D_i \; }[/math] должны хранить элемент i в целевом расположении, но не в исходном. На рис. 1б представлены соответствующие множества [math]\displaystyle{ S_i \; }[/math] и [math]\displaystyle{ D_i \; }[/math]. Предполагается, что [math]\displaystyle{ S_i \ne \empty \; }[/math] и [math]\displaystyle{ D_i \ne \empty \; }[/math] для каждого элемента i. Миграция данных представляет собой перенос данных таким образом, чтобы все множества [math]\displaystyle{ D_i \; }[/math] получили элемент i, изначально находившийся в [math]\displaystyle{ S_i \; }[/math], а задача заключается в минимизации общего времени, необходимого для переносов.

Предположим, что в основе системы лежит полностью связная сеть, а все элементы данных имеют один и тот же размер. Иными словами, перемещение элемента данных с одного диска на другой всегда занимает одно и то же время. Следовательно, миграция осуществляется в несколько раундов. Рассмотрим полудуплексную модель, в которой каждый диск может участвовать в передаче только одного элемента данных – в качестве отправителя либо получателя. Задача заключается в построении графика миграции с минимальным количеством раундов. Использование обходных вершин не допускается (то есть вершин, не являющихся целью операции перемещения, но используемых как промежуточные точки хранения элемента данных), так что все элементы данных направляются только дискам, которым они требуются.

Основные результаты

Хуллер и др. [11] разработали 9,5-аппроксимацию для задачи миграции данных, коэффициент которой был впоследствии улучшен до 6.5 + o(1). Далее мы рассмотрим нижние границы задачи.

Нотация и нижние границы

1. Максимальная полустепень захода ([math]\displaystyle{ \beta \; }[/math]): Пусть [math]\displaystyle{ \beta_j \; }[/math] – количество элементов данных, которые собирается получить диск j. Иными словами, [math]\displaystyle{ \beta_j = | \{i | j \in D_i\} | }[/math]. Тогда [math]\displaystyle{ \beta = max_j \beta_j \; }[/math] является нижней границей оптимума, поскольку диск может получить только один элемент данных в одном раунде.

2. Максимальное количество элементов, источником или назначением которых может быть диск [math]\displaystyle{ (\alpha \; }[/math]): Для каждого элемента i по меньшей мере один диск в [math]\displaystyle{ S_i \; }[/math] должен быть использован в качестве источника элемента, этот диск называется первичным источником. Уникальный первичный источник [math]\displaystyle{ s_i \in S_i \; }[/math] для каждого элемента i, минимизирующий значение [math]\displaystyle{ \alpha = max_{j = 1, ..., N} (| \{ i | j = s_i \} | + \beta_j) \; }[/math], может быть найден при помощи алгоритма вычисления потока в сети. Отметим, что [math]\displaystyle{ \alpha \ge \beta \; }[/math]; [math]\displaystyle{ \alpha \; }[/math] также является нижней границей оптимального решения.

3. Минимальное время, необходимое для клонирования (M): Пусть диск j делает копию элемента i в k-м раунде. В конце m-го раунда количество копий, которые могут быть созданы из этой копии, не превышает [math]\displaystyle{ 2^{m - k} \; }[/math], поскольку в каждом раунде количество копий может только удваиваться. Отметим также, что каждый диск может в одном раунде сделать копию только одного элемента. Поскольку нужно создать не менее [math]\displaystyle{ |D_i| \; }[/math] копий элемента i, минимальное значение m, удовлетворяющее следующей линейной программе, задает нижнюю границу оптимального решения:

L(m):

(1) [math]\displaystyle{ \sum_j \sum_{k = 1}^m 2^{m - k} \; x_{ijk} \ge | D_i| }[/math] для всех i

(2) [math]\displaystyle{ \sum_i x_{ijk} \le 1 }[/math] для всех j, k

(3) [math]\displaystyle{ 0 \le x_{ijk} \le 1 \; }[/math]

Алгоритм миграции данных

9,5-аппроксимацию можно получить следующим образом.

Алгоритм вначале вычисляет множества представителей для каждого элемента и отправляет элемент в множества представителей, которые, в свою очередь, пересылают элемент в оставшееся множество. Множества представителей вычисляются по-разному в зависимости от размера [math]\displaystyle{ D_i \; }[/math].

Представители для больших множеств

Для множеств размером не менее [math]\displaystyle{ \beta \; }[/math] непересекающаяся коллекция множеств представителей [math]\displaystyle{ R_i, i = l, ..., \Delta \; }[/math], должна удовлетворять следующим свойствам:

(1) каждое множество [math]\displaystyle{ R_i \; }[/math] должно быть подмножеством [math]\displaystyle{ D_i \; }[/math],

(2) [math]\displaystyle{ |R_i| = \lfloor| D_i | / \beta \rfloor \; }[/math].

Множества представителей могут быть найдены при помощи алгоритма вычисления потока в сети.

Представители для маленьких множеств

Для каждого элемента i положим [math]\displaystyle{ \gamma_i = | D_i | \; mod \; k }[/math]. Необходимо вычислить вторичного представителя [math]\displaystyle{ r_i \; }[/math] в [math]\displaystyle{ D_i \; }[/math] для элементов с [math]\displaystyle{ \gamma_i \ne 0 \; }[/math]. Диск j может быть вторичным представителем [math]\displaystyle{ r_i \; }[/math] для нескольких элементов, если [math]\displaystyle{ \sum_{i \in I_j} \gamma_i \le 2 \beta - 1 \; }[/math], где [math]\displaystyle{ I_j \; }[/math] – множество элементов, для которых j является вторичным представителем. Это можно сделать при помощи алгоритма Шмойса-Тардош [17] для обобщенной задачи о назначениях.

Планирование миграций

Если имеются представители для всех элементов данных, миграцию можно выполнить в три этапа следующим образом:

1. Миграция в [math]\displaystyle{ R_i \; }[/math]: каждый элемент данных вначале отправляется в множество [math]\displaystyle{ R_i \; }[/math]. Преобразуя дробное решение, приведенное в L(M), можно найти график миграции из [math]\displaystyle{ s_i \; }[/math] в [math]\displaystyle{ R_i \; }[/math], требующий не более [math]\displaystyle{ 2M + \alpha \; }[/math] раундов.

2. Миграция в [math]\displaystyle{ r_i \; }[/math]: элемент i отправляется из первичного источника [math]\displaystyle{ s_i \; }[/math] в [math]\displaystyle{ r_i \; }[/math]. Эту миграцию можно выполнить за [math]\displaystyle{ 1,5 \alpha \; }[/math] раундов при помощи алгоритма раскраски ребер [16].

3. Миграция на оставшиеся диски: Теперь можно создать граф переноса из представителей на оставшиеся диски следующим образом. Для каждого элемента i добавьте ориентированные ребра от дисков в [math]\displaystyle{ R_i \; }[/math] к [math]\displaystyle{ (\beta - 1) \lfloor \frac{|D_i|}{\beta} \rfloor \; }[/math] дисков в [math]\displaystyle{ D_i \backslash R_i \; }[/math], такие, чтобы полустепень выхода каждой вершины в [math]\displaystyle{ R_i \; }[/math] не превышала [math]\displaystyle{ \beta - 1 \; }[/math], а полустепень входа каждой вершины в [math]\displaystyle{ D_i \backslash R_i \; }[/math] из [math]\displaystyle{ R_i \; }[/math] была равна 1. Также добавляется ориентированное ребро от вторичного представителя [math]\displaystyle{ r_i \; }[/math] элемента i к оставшимся дискам в [math]\displaystyle{ D_i \; }[/math], не имеющим входящих ребер из [math]\displaystyle{ R_i \; }[/math]. Было показано, что максимальная степень графа переносов не превышает [math]\displaystyle{ 4 \beta - 5 \; }[/math], а кратность равна [math]\displaystyle{ \beta + 2 \; }[/math]. Следовательно, миграцию из графа переносов можно выполнить за [math]\displaystyle{ 5 \beta - 3 \; }[/math] раундов при помощи алгоритма раскраски ребер мультиграфа [18].

Анализ

Заметим, что общее количество раундов, необходимых для выполнения вышеописанного алгоритма, не превышает [math]\displaystyle{ 2M + 2,5 \alpha + 5 \beta - 3 \; }[/math]. Поскольку [math]\displaystyle{ \alpha \; }[/math], [math]\displaystyle{ \beta \; }[/math] и M являются нижними границами оптимального количества раундов, этот алгоритм дает 9,5-аппроксимацию.

Теорема 1 ([11]). Существует алгоритм 9,5-аппроксимации для задачи миграции данных.

Хуллер и др. [10] позднее улучшили его, получив (6,5 + o(1))-аппроксимацию.

Теорема 2 ([10]). Существует алгоритм (6.5 + o(1))-аппроксимации для задачи миграции данных.

Применение

Миграция данных в системах хранения

Обычно большой сервер, хранящий данные, состоит из нескольких дисков, соединенных в сеть, называемую сетью хранения данных. Для удовлетворения высокого спроса, особенно в случае мультимедийных данных, обычно практикуется репликация объектов данных в рамках системы хранения. У дисков обычно имеются ограничения на объем хранимых данных, а также на количество клиентов, которые могут одновременно обращаться к данным с одного диска. Было разработано несколько аппроксимационных алгоритмов для сопоставления известной потребности в данных с конкретной схемой расположения данных для максимально продуктивного их использования [под использованием понимается общее количество клиентов, которые могут быть назначены диску, содержащему нужные им данные] [4, 8, 14, 15]. Для этого они вычисляют не только количество копий каждого элемента, которые необходимо создать, но и схему расположения, определяющую точное подмножество элементов на каждом диске. Эта задача является NP-полной, однако для нее существуют аппроксимационные схемы с полиномиальным временем выполнения [4, 8, 14]. Если известен относительный спрос на данные, алгоритм вычисляет почти оптимальную схему.

По мере изменения потребности в данных со временем системе необходимо создавать новые схемы расположения. Для удовлетворения высокого спроса на популярные объекты необходимо динамически создавать новые копии и размещать их на разных дисках. Задача миграции данных заключается в вычислении конкретного графика для множества дисков, позволяющего преобразовать изначальную схему расположения в целевую. Миграция должна выполняться насколько возможно быстро, поскольку во время ее выполнения эффективность системы будет ниже оптимальной.

Мгновенный обмен сообщениями и широковещательная передача

Задачу миграции данных можно рассматривать как обобщение задач мгновенного обмена сообщениями и широковещательной передачи. Последние играют важную роль в разработке протоколов коммуникации в сетях различных типов и были многократно исследованы (см., например, [6, 7] и ссылки в этих работах). Задача мгновенного обмена сообщениями выглядит следующим образом. Пусть имеется n человек, и у каждого человека имеется элемент сообщения («слух»), которым он или она желает поделиться со всеми остальными. Коммуникация обычно выполняется поэтапно, и на каждом этапе любой человек может связываться не более чем с одним другим человеком. Некоторые модели коммуникаций допускают полный обмен всеми слухами, известными каждому человеку, на одном этапе. Возможно наличие графа коммуникаций, ребра которого обозначают, между какими парами людей допускается непосредственная коммуникация на каждом этапе. В задаче широковещательной передачи одному человеку необходимо передать слух каждому другому человеку. Задача миграции данных обобщает эти две задачи тремя способами: (1) каждый слух необходимо передать только некоторому подмножеству людей; (2) одному человеку могут быть известны несколько слухов; (3) один и тот же слух изначально может быть известен нескольким людям.

Открытые вопросы

Задача миграции данных является NP-полной в силу редукции задачи раскраски ребер. Однако для этой задачи неизвестны доказательства неаппроксимируемости. На данный момент лучший коэффициент аппроксимации достаточно высок (6,5 + o(1)), и было бы любопытно сузить разрыв между гарантией аппроксимации и неаппроксимируемостью.

Еще один открытый вопрос заключается в объединении задач размещения и миграции данных. Этот вопрос изучали Хуллер и др. [9]. Пусть даны изначальное расположение и новая модель спроса. Задача заключается в поиске серии перемещений данных, которая может быть выполнена за определенное число этапов и обеспечивает наилучшее возможное расположение для имеющейся модели спроса. Они показали, что даже одноэтапная миграция является NP-полной задачей, и предложили эвристический алгоритм для ее решения. Эксперименты показали, что последовательное многократное выполнение одноэтапной миграции дает высокий практический результат. В дальнейшем было бы любопытно получить нетривиальные аппроксимационные алгоритмы для этой задачи.

Еще одно перспективное направление будущих исследований – миграция данных в гетерогенной системе хранения. Большинство исследований миграции данных были посвящены главным образом гомогенным системам хранения и предполагали, что все диски имеют одни и те же фиксированные свойства, а все сетевые соединения – одну и ту же фиксированную пропускную способность. Однако на практике крупные системы хранения могут быть гетерогенными. Например, диски могут иметь разные свойства, поскольку добавляются со временем из-за возросшего спроса на емкость памяти. Лу и др. [13] изучали случай с различной пропускной способностью дисков, связанной с разной нагрузкой. Они использовали подход на базе теории управления для генерации адаптивных коэффициентов миграции данных, обеспечивающих минимальное снижение качества предоставления услуги. Этот алгоритм значительно уменьшает время задержки для клиентов по сравнению с предыдущими схемами. Однако теоретических границ эффективности миграции данных представлено не было. Коффман и др. [2] изучали случай, в котором каждый диск i может одновременно обрабатывать [math]\displaystyle{ p_i \; }[/math] передач, и предложили аппроксимационные алгоритмы. В некоторых статьях [2, 12] рассматривался случай с гетерогенной длиной элементов данных (однако сама система при этом была гомогенной) и были предложены аппроксимационные алгоритмы для этой задачи.

Экспериментальные результаты

Голубчик и др. [3] провели обширное исследование эффективности алгоритмов миграции данных при различных изменениях схем доступа пользователей. Они сравнивали алгоритм 9,5-аппроксимации [11] и несколько других эвристических алгоритмов. Некоторые из этих эвристических алгоритмов не способны предоставить константные гарантии аппроксимации, для других алгоритмов такие гарантии вообще неизвестны. Алгоритм Хуллера и др. [11] имеет коэффициент 9,5 в наихудшем случае, однако в экспериментах количество необходимых раундов превышало нижнюю границу менее чем в 3,25 раз.

Эти исследователи также сформулировали задачу соответствия, в которой вычисляется сопоставление дисков в исходном расположении с дисками в целевом расположении, обеспечивающее минимальное количество изменений. Как показали их эксперименты, хорошее решение задачи соответствия может повысить эффективность алгоритмов миграции данных в 4,4 раза по сравнению с плохим решением.

Ссылка на код

http://www.cs.umd.edu/projects/smart/data-migration/

См. также

• Широковещательная передача в геометрических радиосетях
• Детерминированная широковещательная передача в радиосетях

Литература

Специальный случай задачи миграции данных изучали Андерсон и др. [1] и Холл и др. [5]. Они предположили, что имеется граф переносов данных, вершины которого соответствуют дискам, а ориентированные ребра – каждой обозначенной операции перемещения (создание новых копий элементов данных не допускается). Вычисление графика перемещения данных в точности соответствует задаче раскраски ребер графа переноса. Теперь можно применить алгоритмы раскраски ребер мультиграфов для расчета графика миграции, поскольку каждый класс цветов представляет сопоставление в графе, которое можно спланировать одновременно. Вычисление решения с минимальным количеством раундов является NP-полной задачей, однако для раскраски ребер разработано несколько эффективных аппроксимационных алгоритмов. Задача становится сложнее при наличии ограничений на объем диска. Холл и др. [5] показали, что в предположении, что на каждом диске имеется один свободный элемент памяти, можно разработать очень эффективные аппроксимации с константным коэффициентом. Такие алгоритмы используют не более [math]\displaystyle{ 4 \lceil \Delta / 4 \rceil \; }[/math] цветов и не более n/3 обходных вершин, либо не более [math]\displaystyle{ 6 \lceil \Delta / 4 \rceil \; }[/math] цветов – без обходных вершин.

Большинство результатов задачи миграции данных получены для полудуплексной модели. Еще одна интересная модель коммуникаций – полнодуплексная модель, в которой каждый диск может на каждом этапе выступать в качестве отправителя и получателя одного элемента. Существует алгоритм (4 + o(1))-аппроксимации для полнодуплексной модели [10].

1. Anderson, E., Hall, J., Hartline, J., Hobbes, M., Karlin, A., Saia, J., Swaminathan, R., Wilkes, J.: An experimental study of data migration algorithms. In: Workshop on Algorithm Engineering (2001)

2. Coffman, E., Garey, M., Jr., Johnson, D., Lapaugh, A.: Scheduling file transfers. SIAM J. Comput. 14(3), 744-780 (1985)

3. Golubchik, L., Khuller, S., Kim, Y., Shargorodskaya, S., Wan., Y.: Data migration on parallel disks. In: 12th Annual European Symposium on Algorithms (ESA) (2004)

4. Golubchik, L., Khanna, S., Khuller, S.,Thurimella, R., Zhu, A.: Approximation algorithms for data placement on parallel disks. In: Symposium on Discrete Algorithms, pp. 223-232. Society for Industrial and Applied Mathematics, Philadelphia (2000)

5. Hall, J., Hartline, J., Karlin, A., Saia, J., Wilkes, J.: On algorithms for efficient data migration. In: SODA, pp. 620-629. Society for Industrial and Applied Mathematics, Philadelphia (2001)

6. Hedetniemi, S.M., Hedetniemi, S.T., Liestman, A.: A survey of gossiping and broadcasting in communication networks. Networks 18,129-134 (1988)

7. Hromkovic, J., Klasing, R., Monien, B., Peine, R.: Dissemination of information in interconnection networks (broadcasting and gossiping). In: Du, D.Z., Hsu, F. (eds.) Combinatorial Network Theory, pp. 125-212. Kluwer Academic Publishers, Dordrecht (1996)

8. Kashyap, S., Khuller, S.: Algorithms for non-uniform size data placement on parallel disks. In: Conference on FST&TCS Conference. LNCS, vol. 2914, pp. 265-276. Springer, Heidelberg (2003)

9. Kashyap, S., Khuller, S., Wan, Y-C., Golubchik, L.: Fast reconfiguration of data placement in parallel disks. In: Workshop on Algorithm Engineering and Experiments (2006)

10. Khuller, S., Kim, Y., Malekian, A.: Improved algorithms for data migration. In: 9th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems (2006)

11. Khuller, S., Kim, Y., Wan, Y.-C.: Algorithms for data migration with cloning. SIAM J. Comput. 33(2), 448-461 (2004)

12. Yoo-Ah Kim. Data migration to minimize the average completion time. J. Algorithms 55,42-57 (2005)

13. Lu, C., Alvarez, G.A., Wilkes, J.: Aqueduct:online data migration with performance guarantees. In: Proceedings of the Conference on File and Storage Technologies (2002)

14. Shachnai, H., Tamir, T.: Polynomial time approximation schemes for class-constrained packing problems. J. Sched. 4(6) 313-338(2001)

15. Shachnai, H., Tamir, T.: On two class-constrained versions of the multiple knapsack problem. Algorithmica 29(3), 442-467 (2001)

16. Shannon, C.E.: A theorem on colouring lines of a network. J. Math. Phys. 28,148-151 (1949)

17. Shmoys, D.B., Tardos, E.: An approximation algorithm for the generalized assignment problem. Math. Program. 62(3), 461^74(1993)

18. Vizing,V.G.: On an estimate of the chromatic class of a p-graph (Russian). Diskret. Analiz. 3, 25-30 (1964)