Метрическая задача коммивояжера
Постановка задачи
Задачей коммивояжера (Traveling Salesman Problem, TSP) является следующая задача оптимизации:
Дано: полный неориентированный граф без циклов G = (V, E) и весовая функция [math]\displaystyle{ w: E \to \mathbb{Q}_{ \ge 0} }[/math], присваивающая каждому ребру неотрицательный вес.
Допустимые решения: все гамильтоновы обходы, т.е. подграфы H графа G, которые являются связными и каждая вершина которых имеет степень 2.
Целевая функция: весовая функция [math]\displaystyle{ w(H) = \sum_{e \in H} w(e) \; }[/math] обхода.
Цель: минимизация значения весовой функции.
Задача коммивояжера представляет собой NP-полную задачу. Это означает, что для ее решения не существует алгоритма с полиномиальным временем выполнения, если только не окажется верным P = NP. Одним из способов разрешения этой проблемы являются аппроксимационные алгоритмы. Аппроксимационный алгоритм задачи TSP с полиномиальным временем выполнения называется алгоритмом [math]\displaystyle{ \alpha \; }[/math]-аппроксимации, если обход H, полученный с его помощью, удовлетворяет неравенству [math]\displaystyle{ w(H) \le \alpha \cdot OPT(G) \; }[/math]. Здесь OPT(G) – вес обхода с минимальным весом для графа G. Если граф G понятен из контекста, можно записывать его просто в виде «OPT». Алгоритм [math]\displaystyle{ \alpha \; }[/math]-аппроксимации всегда дает в итоге допустимое решение, целевое значение которого не более чем в [math]\displaystyle{ \alpha \; }[/math] раз отличается от оптимального значения. Коэффициент [math]\displaystyle{ \alpha \; }[/math] также называется коэффициентом аппроксимации или гарантией эффективности. [math]\displaystyle{ \alpha \; }[/math] не обязательно должен быть константой; он может быть функцией, зависящей от размера входного экземпляра или количества вершин n.
Если существует алгоритм с полиномиальным временем выполнения для решения задачи TSP, коэффициент аппроксимации которого зависит от n, то P = NP [6]. Таким образом, следует рассматривать ограниченные экземпляры. Наиболее естественным ограничением является неравенство треугольника, которое выглядит следующим образом:
[math]\displaystyle{ w(u, v) \le w(u, x) + w(x, v) \; }[/math] для всех [math]\displaystyle{ u, v, x \in V \; }[/math].
Соответствующая задача носит название метрической задачи коммивояжера (Metric TSP). Для этой задачи существуют аппроксимационные алгоритмы с константным коэффициентом. Отметим, что для решения метрической задачи коммивояжера достаточно найти обход, который посещает любую вершину не менее одного раза. При наличии такого обхода мы сможем найти гамильтонов обход с меньшим или равным весом, просто пропуская любую вершину, которую мы уже посещали. Согласно неравенству треугольника, вес нового обхода не может возрастать.
Основные результаты
Простой 2-аппроксимацией метрической задачи коммивояжера является алгоритм удвоения дерева. Он использует минимальные остовные деревья для вычисления гамильтоновых обходов. Остовное дерево T графа G = (V, E, w) представляет собой связный ациклический подграф G, содержащий все вершины V. Вес w(T) такого остовного дерева равен сумме весов его ребер, т.е. [math]\displaystyle{ w(T) = \sum_{e \in T} w(e) \; }[/math]. Остовное дерево является минимальным, если его вес минимален среди всех остовных деревьев G. Можно эффективно вычислить минимальное остовное дерево, например, при помощи алгоритмов Прима или Крускала (см., к примеру, [5]).
Алгоритм удвоения дерева известен с давних времен. Следующая лемма необходима для доказательства верхней границы гарантии эффективности алгоритма удвоения дерева.
Дано: полный неориентированный граф без циклов G = (V, E, w) с взвешенными ребрами и весовой функцей [math]\displaystyle{ w: E \to \mathbb{Q}_{ \ge 0} }[/math], удовлетворяющей неравенству треугольника.
Требуется: найти гамильтонов обход для G, являющийся 2-аппроксимацией.
1: Вычислить минимальное остовное дерево T графа G.
2: Продублировать каждое ребро T и получить эйлеров мультиграф T’.
3: Вычислить эйлеров обход для T' (например, при помощи поиска в глубину по T). При посещении вершины эйлерова обхода, которая ранее уже была посещена, пропускаем эту вершину
и переходим к следующей непосещенной вершине эйлерова обхода. (Этот процесс называется сокращением обхода).
Вернуть полученный гамильтонов обход H.
Алгоритм 1. Алгоритм удвоения дерева
Лемма 1. Пусть T – минимальное остовное дерево G = (V, E, w). Тогда [math]\displaystyle{ w(T) \le OPT \; }[/math].
Доказательство. Если удалить любое ребро гамильтонова обхода G, получим остовное дерево G. [math]\displaystyle{ \Box }[/math]
Теорема 2. Алгоритм 1 всегда возвращает гамильтонов обход, вес которого не более чем вдвое превышает вес оптимального обхода. Он имеет полиномиальное время выполнения.
Доказательство. Согласно лемме 1, [math]\displaystyle{ w(T) \le OPT \; }[/math]. Поскольку мы удваиваем каждое ребро T, вес T' составляет [math]\displaystyle{ w(T') = 2w(T) \le 2 OPT \; }[/math]. В результате сокращения обхода на шаге 3 путь в T' заменяется одним ребром. Согласно неравенству треугольника, сумма весов ребер на таком пути не меньше веса ребра, которым он заменяется. (Для произвольных весовых функций данный алгоритм оказывается недействительным). Следовательно, [math]\displaystyle{ w(H) \le w(T') \; }[/math]. Это доказывает утверждение по поводу эффективности аппроксимации.
Время выполнения определяется главным образом временем вычисления минимального остовного дерева – которое, очевидно, является полиномиальным. [math]\displaystyle{ \Box }[/math]
Алгоритм Кристофидеса (алгоритм 2) представляет собой продуманное уточнение алгоритма удвоения дерева. Вначале он вычисляет минимальное остовное дерево. Затем для всех вершин, имеющих нечетную степень в T, он вычисляет совершенное паросочетание с минимальным весом. Паросочетание M для графа G называется паросочетанием на [math]\displaystyle{ U \subseteq V \; }[/math], если все ребра M состоят из двух вершин подмножества U. Такое паросочетание называется совершенным, если каждая вершина из U инцидентна ребру из M.
Дано: полный неориентированный граф без циклов G = (V, E, w) с взвешенными ребрами и весовой функцей [math]\displaystyle{ w: E \to \mathbb{Q}_{ \ge 0} }[/math], удовлетворяющей неравенству треугольника. Требуется: найти гамильтонов обход для G, являющийся 3/2-аппроксимацией. 1: Вычислить минимальное остовное дерево T графа G. 2: Пусть [math]\displaystyle{ U \subseteq V \; }[/math] – множество всех вершин, имеющих нечетную степень в T. Для графа G вычислить совершенное паросочетание с минимальным весом M на U. 3: Вычислить эйлеров обход для [math]\displaystyle{ T \cup M \; }[/math] (рассматриваемый как мультиграф). 4: Выполнить сокращение путей этого эйлерова обхода до гамильтонова обхода H.
Алгоритм 2. Алгоритм Кристофидеса
Лемма 3. Пусть [math]\displaystyle{ U \subseteq V \; }[/math], #U четно. Пусть M – совершенное паросочетание с минимальным весом на U. Тогда [math]\displaystyle{ w(M) \le OPT/2 \; }[/math].
Доказательство. Пусть H – оптимальный гамильтонов обход на G. Выполняем сокращения в H, получая обход H' на [math]\displaystyle{ G|_U \; }[/math] следующим образом: H порождает перестановку вершин в U, представляющую собой порядок, в котором они посещаются по ходу H. Соединим вершины U в порядке, заданном перестановкой. Каждому ребру в H' соответствует путь в H, соединяющий две вершины этого ребра. Согласно неравенству треугольника, [math]\displaystyle{ w(H') \le w(H) \; }[/math]. Поскольку #U является четным, H' представляет собой объединение двух паросочетаний. Вес более легкого из них не превышает [math]\displaystyle{ w(H')/2 \le OPT/2 \; }[/math]. [math]\displaystyle{ \Box }[/math]
Можно вычислить совершенное паросочетание с минимальным весом за время [math]\displaystyle{ O(n^3) \; }[/math]; см., например, [5].
Теорема 4. Алгоритм 2 представляет собой алгоритм 3/2-аппроксимации с полиномиальным временем выполнения.
Доказательство. Вначале отметим, что количество вершин с нечетной степенью в остовном дереве является четным, поскольку сумма степеней всех вершин равна 2(n - 1), а это четное число. Таким образом, совершенное паросочетание на U существует. Вес эйлерова обхода, очевидно, составляет w(T) + w(M). Согласно лемме 1, [math]\displaystyle{ w(T) \le OPT \; }[/math]. Согласно лемме 3, [math]\displaystyle{ w(M) \le OPT/2 \; }[/math]. Вес w(H) вычисленного обхода H не превышает веса эйлерова обхода согласно неравенству треугольника, т.е. [math]\displaystyle{ w(H) \le \frac{3}{2} OPT \; }[/math]. Таким образом, полученный алгоритм представляет собой алгоритм 3/2-аппроксимации, а его время выполнения составляет [math]\displaystyle{ O(n^3) \; }[/math]. [math]\displaystyle{ \Box }[/math]
Применение
Экспериментальный анализ показывает, что алгоритм Кристофидеса сам отклоняется от оптимального обхода на величину от 10 до 15% [3]. Однако он может служить хорошей отправной точкой для других эвристик обхода – таких как эвристика Лина-Кернигана.
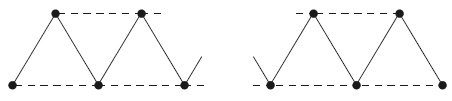
Рисунок 1. Пример для алгоритма Кристофидеса. В графе 2n + 1 вершин. Сплошные ребра имеют вес 1, пунктирные – вес [math]\displaystyle{ 1 + \epsilon \; }[/math].
Открытые вопросы
Анализ алгоритма 2 несложен. Примером может служить метрическое пополнение графа, изображенного на рис. 1. Его единственное минимальное остовное дерево состоит из всех сплошных ребер. Оно содержит только две вершины с нечетными степенями. Ребро между этими двумя вершинами имеет вес [math]\displaystyle{ (1 + \epsilon)(n + 1) \; }[/math]. Сокращения путей не требуется; вес обхода, вычисленного алгоритмом, равен [math]\displaystyle{ \approx 3 n \; }[/math]. Оптимальный обход состоит из всех пунктирных ребер, а также самого левого и самого правого сплошных ребер. Вес этого обхода составляет [math]\displaystyle{ (2n - 1)(1 + \epsilon) + 2 \approx 2n \; }[/math].
Вопрос о существовании аппроксимационного алгоритма с лучшей гарантией эффективности является главным нерешенным вопросом в теории аппроксимационных алгоритмов.
Хельд и Карп [2] разработали алгоритм на основе линейного программирования, вычисляющий нижнюю границу веса оптимального обхода для задачи коммивояжера. Была предложена гипотеза, что вес оптимального обхода для задачи коммивояжера не более чем в 4/3 раза превышает его нижнюю границу; однако эта гипотеза уже более 30 лет остается недоказанной. Алгоритмическое доказательство гипотезы позволило бы получить алгоритм 4/3-аппроксимации для метрической задачи коммивояжера.
Экспериментальные результаты
В работе [3] было отмечено отклонение в 10-15% от оптимального (точнее говоря, от границы Хельда-Карпа) на различных экземплярах задачи.
Наборы данных
На странице 8-го тура задач по реализации DIMACS по адресу http://www.research.att.com/~dsj/chtsp/ можно найти множество экземпляров.
См. также
Литература
Кристофидес не публиковал самостоятельно свой алгоритм. Он обычно цитируется по одному из двух технических отчетов Университета Карнеги-Меллона – TR 388 Института индустриальных исследований (теперь он называется Школой бизнеса Теппера) и CS-93-13. Ни один из них в настоящее время не доступен в Университете Карнеги-Меллона [из личной переписки с Фрэнком Бальбахом Balbach, 2006 г.]. В материалах конференции были приведены тезисы объемом в 1 страницу. Однако алгоритм быстро проложил себе дорогу в учебники по теории алгоритмов; см., например, [7].
1. Christofides, N.: Worst case analysis of a new heuristic for the traveling salesman problem, Technical Report 388, Graduate School of Industrial Administration, Carnegie-Mellon University, Pittsburgh, (1976). Also: Carnegie-Mellon University Technical Report CS-93-13, 1976. Abstract in Traub, J.F. (ed.) Symposium on new directions and recent results in algorithms and complexity, pp. 441. Academic Press, New York (1976)
2. Held, M., Karp, R.M.: The traveling salesman problem and minimum spanning trees. Oper. Res. 18,1138-1162 (1970)
3. Johnson, D.S., McGeoch, L.A.: Experimental analysis of heuristics for the STSP. In: Gutin, G., Punnen, A.P. (eds.) The Traveling Salesman Problem and its Variations. Kluwer, Dordrecht (2002)
4. Lawler, E.L., Lenstra, J.K., Rinnooy Kan, A.H.G., Shmoys, D.B. (eds.): The Traveling Salesman Problem. A Guided Tour of Combinatorial Optimization. Wiley, Chichester (1985)
5. Papadimitriou, C., Steiglitz, K.: Combinatorial Optimization: Algorithms and Complexity. Prentice-Hall, Englewood Cliffs (1982)
6. Sahni, S., Gonzalez, T.: P-complete approximation problems. J.ACM 23, 555-565 (1976)
7. Vazirani,V.V.: Approximation Algorithms. Springer, Berlin (2001)
8. Traveling Salesman Problem. www.tsp.gatech.edu (2006). Accessed 28 Mar 2008