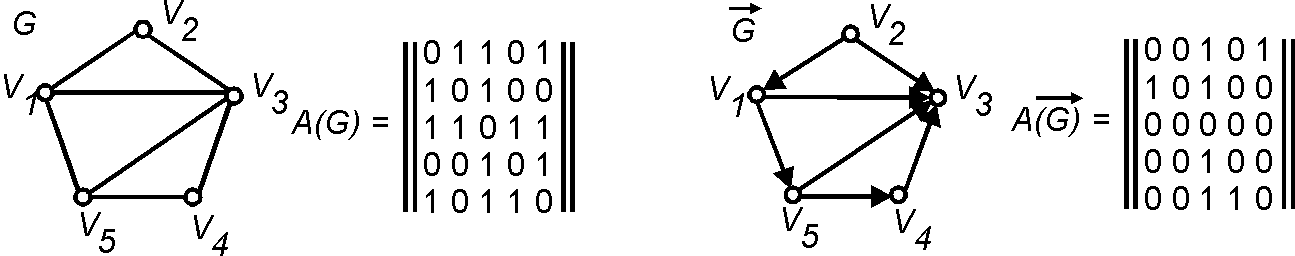Матрица смежности
Матрица смежности (Adjacency matrix, connectivity matrix, vertex incidence matrix) — [math]\displaystyle{ \,(0,1) }[/math]-матрица [math]\displaystyle{ \,A(G) }[/math] размером [math]\displaystyle{ n \times n }[/math] ([math]\displaystyle{ \,n }[/math] — число вершин в [math]\displaystyle{ \,G }[/math]), [math]\displaystyle{ \,(i,j) }[/math]-й элемент [math]\displaystyle{ \,a_{ij} }[/math] которой равен [math]\displaystyle{ \,1 }[/math], если вершины [math]\displaystyle{ \,v_{i} }[/math] и [math]\displaystyle{ \,v_{j} }[/math] смежны, т.е. соединены дугой (или ребром) [math]\displaystyle{ \,(v_{i}, v_{j}) }[/math] и равен [math]\displaystyle{ \,0 }[/math] в противном случае. Для неориентированного графа матрица смежности есть симметричная матрица с нулями на главной диагонали. В матрице смежности для мультиграфов и псевдографов [math]\displaystyle{ \,(i,j) }[/math]-й элемент равен числу ребер, соединяющих вершины [math]\displaystyle{ \,v_{i} }[/math]и [math]\displaystyle{ \,v_{j} }[/math] (при этом петля считается как два ребра).
Матрица смежности определяет граф (орграф, мультиграф, псевдограф) с точностью до изоморфизма.
См. также
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.