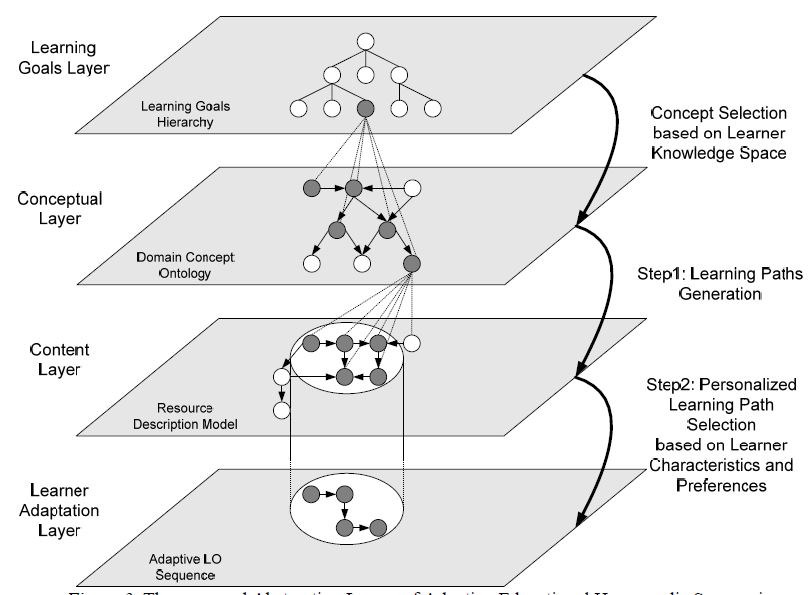
Граф путей концептов

Граф путей концептов (Concepts Path Graph (CPG))

Граф путей концептов - бесконтурный орграф, который представляет множество правил упорядочения, которые определяют последовательность концептов.

Граф путей концептов представляет структуру концептов онтологии предметной области, соответствующей рассматриваемой цели обучения. Концепты, содержащиеся в графе путей концептов выбираются, основываясь на связи между иерархией целей обучения и онтологией предметной области. Структура графа полностью копирует структуру онтологии предметной области. Граф путей концептов - простой бесконтурный орграф, то есть, орграф, не имеющий множественных вершин. Это означает, что каждый концепт содержится только раз в графе путей концептов. Кроме этого, граф путей концептов - бесконтурный орграф, то есть орграф, не содержащий циклов. Это означает, что в любой возможной последовательности концептов, представленной в графе путей концептов, каждый концепт имеет единственное вхождение.

Литература

• Carchiolo V., Longheu A., Malgeri M., Mangioni G. Automatic generation of learning paths. — In Proceedings of the 10th IEEE International Conference on Electronics, Circuits and Systems ICECS 2003, IEEE, Vol. 3 (2003), 1236–1239.
• Karampiperis P., Sampson D. Adaptive learning resources sequencing in educational hypermedia systems. — Educational Technology & Society, 8, 4 (2005), 128–147.
• Pukkhem N., Evens M.W., Vatanawood W. The Concept Path Combination Model for Supporting a Personalized Learning Path in Adaptive Educational Systems. — In the Proceedings of the 2006 International Conference on e-Learning, e-Business, Enterprise Information Systems, e-Government, and Outsourcing (EEE’06), (2006), 10-16.
• Grubišić A., Stankov S., Žitko B. Adaptive Courseware: A Literature Review. — Journal of Universal Computer Science, vol. 21, no. 9 (2015), 1168-1209.