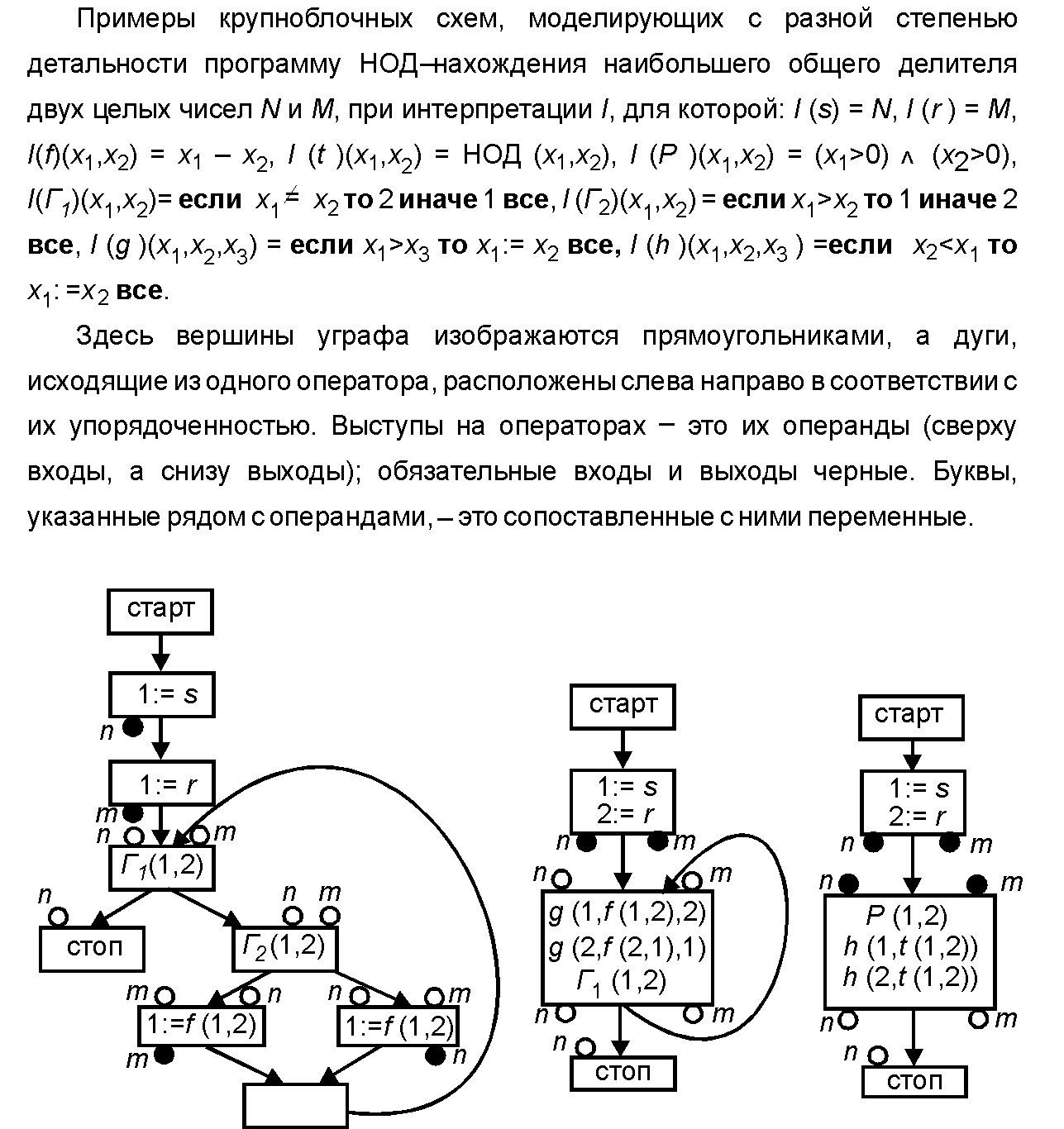
Крупноблочная схема программ

Крупноблочная схема программ (Large-block program schemata) — операторная схема программ, которая рассматривает моделируемую программу в виде совокупности структурных операторов, обрабатывающих структурные значения совокупности переменных. Введена в литературу В.Н.Касьяновым в 1980 г.

Базис $\,\Sigma$, над которым строятся схемы, содержит символы переменных, операций, доступов, предикатов выполнимости, выбора и операндов: обязательных и необязательных входов и выходов. Крупноблочная схема $\,\alpha$ — это тройка

$\,(G_{\alpha}, R_{\alpha},\Omega_{\alpha}),$

в которой $\,G_{\alpha}$ — управляющий граф (уграф), $\,R_{\alpha}$ — раскраска операндов операторов из $\,G_{\alpha},$ сопоставляющая с каждым операндом некоторую переменную, а $\,\Omega_{\alpha}$ — множество интерпретаций.

Переменные, поставленные в соответствие входам операторов, называются их аргументами, а выходам — результатами. Аргументы и результаты разделяются на обязательные и необязательные в зависимости от того, являются ли таковыми операнды, с которыми они сопоставлены.

Каждая интерпретация $\,I\in\Omega_{\alpha}$ — это совокупность, состоящая из области интерпретации $\,D_I$ и двух функций. Одна из них ставит в соответствие элементам базиса $\,\Sigma$ элементы $\,D_I$ и функции, заданные на $\,D^r_I$, а вторая — выделяет используемые и неиспользуемые части аргументов интерпретирующих функций при вычислении указанных частей их результатов. Предполагается, что $\,D_I$ может содержать как простые значения, так и составные. Каждое из составных значений — это множество упорядоченных пар элементов из $\,D_I$, попарно различающихся по первым компонентам и называемых именами. Таким образом, одно значение может образовывать нетривиальную часть другого значения с некоторым адресом, представляющим собой последовательность имен.

Оператор (в общем случае) — это совокупность, состоящая из слова применимости — выражения, описывающего условия применимости оператора и построенного из обязательных входов и операций, слова выбора — выражения, построенного из входов и операций и описывающего правила выбора той из исходящих дуг, по которой будет осуществлен переход, а также из множества обязательных и необязательных присваиваний, описывающих правила перевычисления состояния памяти. Обязательное присваивание имеет вид $\,a:=F$, где $\,a$ — получатель (обязательный выход), а $\,F$ — источник, представляющий собой выражение, построенное из входов и операций и описывающее правило вычисления значения, которое будет присвоено переменной $\,R(a)$. Необязательное присваивание имеет вид

$g(F_1,\ldots, F_r, F, a),$

где $\,g$ — символ доступа, $\,a$ — получатель (необязательный выход), $\,F$ — источник, $F_1,\ldots,F_r$ — ключи, представляющие собой выражения, построенные из входов и операций. В зависимости от интерпретации $\,g$ и текущих значений ключей определены используемые и неиспользуемые части переменной $\,x=R(a)$. Необязательное присваивание сохраняет значения используемой части $\,x$ и перевычисляет неиспользуемую часть $\,x$, размещая в ней используемые части значения результата источника.

Крупноблочная модель программ вместе с концепцией крупноблочного моделирования одних схем другими дает единую позицию для комплексного исследования оптимизирующих преобразований программ со структурами данных и действий и их применения в системах конструирования программ. Существенными свойствами, отличающими класс крупноблочных схем от других моделей программ, являются его универсальность в смысле широты описания класса последовательных программ и способов их оптимизации, а также его полнота — возможность построения по любой крупноблочной схеме (в частности, программе) и любому ее укрупнению операторов и переменных такой другой крупноблочной схемы, которая моделирует исходную при заданном ее укрупнении.

См. также

• Неинтерпретированные схемы,
• Стандартные схемы,
• Схема программ,
• Схема с косвенной адресацией,
• Схема с распределенной памятью,
• Схемы Мартынюка.

Литература

• Касьянов В.Н. Теоретико-графовые задачи анализа управляющих графов транслируемых программ // Исследования по прикладной теории графов. — Новосибирск: Наука. Сиб. отд-ние, 1986.

• Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.