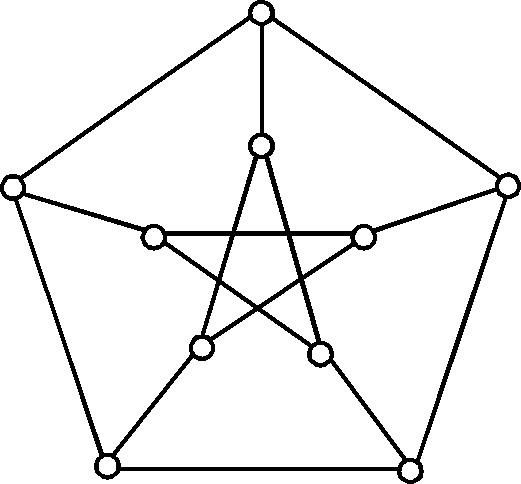
Граф Петерсена

Граф Петерсена (J.Petersen, 1891) — граф $P_{10}( = P)$, допускающий следующее представление:

Пусть $\Omega = \{1,2,3,4,5\}$ — 5-элементное множество. Вершины графа $P_{10}$ — это двухэлементные подмножества из $\Omega$. Две вершины в $P_{10}$ смежны тогда и только тогда, когда соответствующие им подмножества не пересекаются. Граф Петерсена представляет собой сумму 1-фактора и 2-фактора, состоящего из двух 5-циклов. Граф Петерсена есть наименьший 3-регулярный граф с обхватом 5, без гамильтонова цикла, с повышенным хроматическим числом.

Гиперсетью Петерсена называется граф $HP_{n} = Q_{n-3} \times P$, где $Q_{n-3}$ — $(n-3)$-мерный гиперкуб.

$n$-складной граф Петерсена ($n$-folded Petersen graph) есть граф $FP_{n} = \underbrace{P \times \cdots \times P}_{n}$. Здесь $\times$ обозначает декартово произведение.

Литература

• Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.

• Харари Ф. Теория графов. — М.: Мир, 1973.

• Workshop. Utrecht, 1993 // Lect. Notes Comp. Sci., 1994, vol. 790.