Рандомизированная широковещательная передача в радиосетях

Ключевые слова и синонимы

Многоскачковые радиосети (Multi-hop radio networks); децентрализованные сети (Ad hoc networks)

Постановка задачи

В данной статье исследуются детерминированные и рандомизированные протоколы для обеспечения широковещательной передачи (распространения сообщения от источника ко всем другим узлам) в произвольных многоскачковых синхронных радиосетях.

Модель состоит из произвольной (неориентированной) сети, процессоры которой общаются в синхронных временных интервалах, подчиняясь следующим правилам. В каждом временном интервале каждый процессор выступает либо в роли передатчика, либо в роли приемника. Мы говорим, что процессор, выступающий в роли приемника, получает сообщение во временном интервале [math]\displaystyle{ t }[/math], если ровно один из его соседей ведет передачу в этом временном интервале. Полученное сообщение соответствует переданному. Если в данном временном интервале несколько соседей ведут передачу, возникает конфликт. В этом случае приемник может либо получить сообщение от одного из передающих соседей, либо не получить никакого сообщения. Предполагается, что конфликты (или коллизии) необнаружимы, поэтому процессор не может отличить случай, когда ни один сосед не ведет передачу, от случая, когда два или более его соседей передают в этом временном интервале. Процессоры не обязаны иметь идентификаторы и не знают своих соседей; в частности, процессорам неизвестна топология сети.

Единственными входными данными, необходимыми протоколу, являются [math]\displaystyle{ n }[/math] – количество процессоров в сети, [math]\displaystyle{ \Delta }[/math] – априорно известная верхняя граница максимальной степени сети и граница ошибки – [math]\displaystyle{ \epsilon }[/math]. (Все границы априорно известны алгоритму).

Широковещательная передача – это задача, инициируемая одним процессором, называемым источником, который передает одно сообщение. Цель состоит в том, чтобы сообщение достигло всех процессоров в сети.

Основные результаты

Основным результатом является рандомизированный протокол, который обеспечивает широковещательную передачу за время, оптимальное с точностью до логарифмического множителя. В частности, с вероятностью [math]\displaystyle{ 1 - \epsilon }[/math] протокол обеспечивает широковещательную передачу за [math]\displaystyle{ O((D + log \; n / \epsilon) \cdot log \; n) }[/math] временных интервалов.

С другой стороны, была доказана линейная нижняя граница временной сложности широковещательной передачи в детерминированном варианте. А именно, любой детерминированный протокол широковещательной передачи требует [math]\displaystyle{ \Omega(n) }[/math] временных интервалов, даже если сеть имеет диаметр 3, а [math]\displaystyle{ n }[/math] известно всем процессорам. Эти два результата демонстрируют экспоненциальный разрыв в сложности между рандомизацией и детерминизмом.

Рандомизированные протоколы

Процедура Decay

Основная идея, используемая в протоколе, заключается в разрешении потенциальных конфликтов путем случайного исключения половины передатчиков. Этот процесс «урезания наполовину» повторяется каждый временной интервал в надежде, что будет существовать временной интервал с одним активным передатчиком. Процесс «урезания наполовину» легко реализовать распределенным образом, позволив каждому процессору случайным образом решать, исключать ли себя. Далее будет показано, что если все соседи приемника следуют процедуре исключения, то с положительной вероятностью существует временной интервал, в котором передачу ведет ровно один сосед.

Далее следует описание процедуры отправки сообщения m, которая выполняется каждым процессором после получения m:

  procedure Decay(k, m);
  repeat не более k раз (но не менее одного раза!)
    отправить m всем соседям;
    задать значение броска монеты coin равным 0 или 1 с равной вероятностью, 
  until coin = 0.

Используя элементарные вероятностные аргументы, можно доказать следующую теорему:

Теорема 1. Пусть [math]\displaystyle{ y }[/math] – вершина из [math]\displaystyle{ G }[/math]. Пусть [math]\displaystyle{ d \ge 2 }[/math] соседей [math]\displaystyle{ y }[/math] выполняют процедуру Decay в течение интервала времени [0, k) (предполагается, что все они начинают выполнение в Time = 0). Тогда [math]\displaystyle{ P(k, d) }[/math] – вероятность того, что [math]\displaystyle{ y }[/math] получит сообщение к моменту Time = k – удовлетворяет следующим свойствам:

1. [math]\displaystyle{ lim_{k \to \infty} P(k, d) \ge 2/3 }[/math];

2. для [math]\displaystyle{ k \ge 2 \lceil log \; d \rceil }[/math] верно [math]\displaystyle{ P(k, d) \gt 1/2 }[/math].

(Все логарифмы приведены к основанию 2).

Ожидаемое время завершения алгоритма зависит от вероятности того, что coin = 0. Здесь эта вероятность равна половине. Анализ преимуществ использования других вероятностей был проведен Хофри в работе [4].

Протокол широковещательной передачи (Broadcast)

Протокол широковещательной передачи выполняет несколько вызовов процедуры Decay(k, m). Согласно теореме 1 (2), чтобы вероятность получения сообщения процессором [math]\displaystyle{ y }[/math] была не ниже 1/2, параметр [math]\displaystyle{ k }[/math] должен быть не меньше [math]\displaystyle{ 2 \; log \; d }[/math] (где [math]\displaystyle{ d }[/math] – число соседей, посылающих сообщение процессору [math]\displaystyle{ y }[/math]). Поскольку [math]\displaystyle{ d }[/math] неизвестно, параметр был выбран равным [math]\displaystyle{ k = 2 \lceil log \; \Delta \rceil }[/math] (напомним, что параметр [math]\displaystyle{ \Delta }[/math] был определен как верхняя граница полустепени захода). Теорема 1 также требует, чтобы все участники начинали выполнять процедуру Decay в один и тот же временной интервал. Поэтому Decay запускается только при целочисленных кратных [math]\displaystyle{ 2 \lceil log \; \Delta \rceil }[/math].

  procedure Broadcast;
  [math]\displaystyle{ k = 2 \lceil log \; \Delta \rceil }[/math];
  [math]\displaystyle{ t = 2 \lceil log(N / \epsilon \rceil }[/math];
  дождаться получения сообщения, скажем m;
  выполнить t раз {
    дождаться (Time mod k) = 0;
  Decay(k, m); }

Считается, что сеть выполняет схему широковещательной передачи Broadcast_scheme, если некоторый процессор, обозначаемый s, передает начальное сообщение, и каждый процессор выполняет описанную выше процедуру Broadcast.

Теорема 2. Пусть [math]\displaystyle{ T = 2D + 5 max \{ \sqrt{D}, \sqrt{log(n / \epsilon}) \} \cdot \sqrt{log(n / \epsilon}) }[/math]. Предположим, что Broadcast_scheme запускается в момент времени Time = 0. Тогда с вероятностью выше [math]\displaystyle{ 1 - 2 \epsilon }[/math] к моменту времени [math]\displaystyle{ 2 \lceil log \; \Delta \rceil \cdot T }[/math] все узлы получат сообщение. Более того, с вероятностью выше [math]\displaystyle{ 1 - 2 \epsilon }[/math] все узлы завершат работу к моменту времени [math]\displaystyle{ 2 \lceil log \; \Delta \rceil \cdot (T + \lceil log(N / \epsilon) \rceil ) }[/math].

Граница, приведенная в теореме 2, содержит два аддитивных члена: первый представляет собой диаметр сети, а второй – задержки, вызванные конфликтами (которые возникают редко, но все же имеют место).

Дополнительные свойства протокола широковещательной передачи:

• Идентификаторы процессоров: протокол не использует идентификаторы процессоров и, следовательно, не требует, чтобы процессоры имели различные идентификаторы (или чтобы они знали идентификаторы своих соседей). Более того, процессор даже не обязан знать количество своих соседей. Это свойство делает протокол адаптивным к изменениям топологии, происходящим на протяжении выполнения, и устойчивым к незлонамеренным сбоям.

• Знание размера сети: протокол работает почти так же хорошо, если вместо фактического числа процессоров (т. е. [math]\displaystyle{ n }[/math]) дать «хорошую» верхнюю границу этого числа (обозначается [math]\displaystyle{ N }[/math]). Верхняя граница, полиномиальная от [math]\displaystyle{ n }[/math], дает ту же самую временную сложность с поправкой на константный коэффициент (поскольку сложность логарифмически зависит от [math]\displaystyle{ N }[/math]).

• Обнаружение конфликтов: алгоритм и его сложность остаются действительными, даже если при возникновении конфликта не может быть получено ни одного сообщения.

• Простота и быстрота локальных вычислений: в каждый временной интервал каждый процессор выполняет постоянный объем локальных вычислений.

• Сложность по числу сообщений: каждый процессор активен в течение [math]\displaystyle{ \lceil log(N / \epsilon) \rceil }[/math] последовательных фаз, а среднее число передач за фазу составляет не более 2. Таким образом, ожидаемое число передач всей сети ограничено [math]\displaystyle{ 2n \cdot \lceil log(N / \epsilon) \rceil }[/math].

• Адаптивность к изменению топологии и отказоустойчивость: протокол устойчив к некоторым изменениям в топологии сети. Например, ребра могут быть добавляться или удаляться в любое время, при условии, что сеть неизменных ребер остается связной. Это соответствует отказам или остановке работы ребер, так что система демонстрирует устойчивость к некоторым незлонамеренным сбоям.

• Ориентированные сети: протокол не использует подтверждения. Таким образом, он может применяться даже тогда, когда каналы связи не симметричны; иначе говоря, тот факт, что процессор [math]\displaystyle{ v }[/math] может передать сообщение процессору [math]\displaystyle{ u }[/math], не означает, что [math]\displaystyle{ u }[/math] может передать сообщение [math]\displaystyle{ v }[/math]. (Соответствующей моделью сети, таким образом, является ориентированный граф). В реальной жизни такая ситуация возникает, например, когда [math]\displaystyle{ v }[/math] имеет более мощный передатчик, чем [math]\displaystyle{ u }[/math].

Нижняя граница для детерминированных алгоритмов

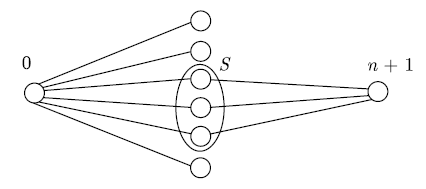
Для детерминированных алгоритмов можно продемонстрировать нижнюю границу: для любого [math]\displaystyle{ n }[/math] существует семейство [math]\displaystyle{ n }[/math]-узловых сетей, такое, что каждая детерминированная широковещательная схема требует [math]\displaystyle{ \Omega(n) }[/math] времени. Для любого непустого подмножества [math]\displaystyle{ S \subseteq \{1, 2, ...n \} }[/math] рассмотрим следующую сеть [math]\displaystyle{ G_s }[/math] (рис. 1).

Рисунок 1. Сеть, используемая для получения нижней границы

Узел 0 является источником, а узел n + 1 – стоком. Источник инициирует сообщение, и задача широковещательной передачи в [math]\displaystyle{ G_S }[/math] заключается в том, чтобы достичь стока. Сложность проистекает из того факта, что разбиение среднего уровня (т. е. [math]\displaystyle{ S }[/math]) не известно заранее. Следующая теорема может быть доказана путем ряда сокращений до определенной «игры на попадание»:

Теорема 3. Каждый детерминированный протокол широковещательной передачи, корректный для всех [math]\displaystyle{ n }[/math]-узловых сетей, требует [math]\displaystyle{ \Omega(n) }[/math] времени.

В работе [2] была допущена некоторая путаница в отношении модели широковещательной передачи. В ней ошибочно утверждалось, что нижняя граница справедлива и тогда, когда коллизия неотличима от отсутствия передачи. Ковальски и Пелц [5] опровергли это утверждение, показав, как можно вести широковещательную передачу за логарифмическое время во всех сетях типа [math]\displaystyle{ G_S }[/math].

Применение

Процедура Decay использовалась для разрешения соперничества устройств в радиосетях и сетях сотовой связи.

См. также

• Широковещательная передача в геометрических радиосетях
• Коммуникация в децентрализованных мобильных сетях с использованием метода случайного блуждания
• Детерминированная широковещательная передача в радиосетях
• Рандомизированный мгновенный обмен сообщениями в радиосетях

Литература

Последующие работы продемонстрировали оптимальность рандомизированного алгоритма:

• Алон и др. [1] доказали существование семейства сетей радиуса 2 с [math]\displaystyle{ n }[/math] вершинами, для которых любое расписание широковещательной передачи требует не менее [math]\displaystyle{ \Omega(log^2 \; n) }[/math] временных слотов.

• Кушилевиц и Мансур [7] показали, что для любого рандомизированного широковещательного протокола существует сеть, в которой ожидаемое время передачи сообщения равно [math]\displaystyle{ \Omega(D \; log(N/D)) }[/math].

• Бруски и Дель Пинто [3] показали, что для любого детерминированного алгоритма распределенной трансляции, любых [math]\displaystyle{ n }[/math] и [math]\displaystyle{ D \le n/2 }[/math] существует сеть с [math]\displaystyle{ n }[/math] узлами диаметром [math]\displaystyle{ D }[/math], такая, что время, необходимое для широковещательной передачи, равно [math]\displaystyle{ \Omega(D \; log \; n) }[/math].

• Ковальски и Пелц [6] обсудили сети, в которых коллизии неотличимы от отсутствия передачи. Они представили нижнюю границу [math]\displaystyle{ \Omega(n \; log \; n/log(n/D)) }[/math] и верхнюю границу [math]\displaystyle{ O(n \; log \; n) }[/math]. Для этой модели они также предложили рандомизированный алгоритм [math]\displaystyle{ O(D \; log \; n + log^2 \; n) }[/math], подтвердив нижнюю границу из [1] и улучшив границу из работы [2] для графов, для которых [math]\displaystyle{ D = \theta(n/log \;n) }[/math].

1. Alon, N., Bar-Noy, A., Linial, N., Peleg,D.: A lower bound for radio broadcast. J. Comput. Syst. Sci. 43(2), 290-298 (1991)

2. Bar-Yehuda, R., Goldreich, O., Itai, A.: On the time-complexity of broadcast in multi-hop radio networks: An exponential gap between determinism and randomization. J. Comput. Syst. Sci. 45(1),104-126(1992)

3. Bruschi, D., Del Pinto, M.: Lower bounds for the broadcast problem in mobile radio networks. Distrib. Comput. 10(3), 129-135(1997)

4. Hofri, M.: A feedback-less distributed broadcast algorithm for multihop radio networks with time-varying structure. In: Computer Performance and Reliability, pp. 353-368. (1987)

5. Kowalski, D.R., Pelc, A.: Deterministic broadcasting time in radio networks of unknown topology. In: FOCS '02: Proceedings of the 43rd Symposium on Foundations of Computer Science, Washington, DC, USA, pp. 63-72. IEEE Computer Society (2002)

6. Kowalski, D.R., Pelc, A.: Broadcasting in undirected ad hoc radio networks. Distrib. Comput. 18(1), 43-57 (2005)

7. Kushilevitz, E., Mansour, Y.: An Q(d\oq(n/d)) lower bound for broadcast in radio networks. In: PODC, 1993, pp. 65-74