Протяженность геометрических сетей
Ключевые слова и синонимы
Обход; коэффициент растяжения; показатель растяжения
Постановка задачи
Нотация
Пусть G = (V, E) – плоская геометрическая сеть, множество вершин V которой является конечным множеством местоположений точек в пространстве [math]\displaystyle{ \mathbb{R}^2 \; }[/math], связанных множеством ребер E, состоящим из непересекающихся прямолинейных отрезков с конечными точками в V. Обозначим для двух точек [math]\displaystyle{ p \ne q \in V \; }[/math] за [math]\displaystyle{ \xi_G (p,q) \; }[/math] кратчайший путь из p в q в сети G. Тогда
(1) [math]\displaystyle{ \sigma (p,q) := \frac{| \xi_G (p,q) |}{|pq|} }[/math]
представляет собой обход, по которому необходимо идти при перемещении по сети G из точки p в точку q, вместо того чтобы пройти напрямую. Здесь |.| обозначает евклидову длину.
Протяженность сети G задается следующим образом:
(2) [math]\displaystyle{ \sigma(G) := max_{p \ne q \in V} \; \sigma(p, q) }[/math]
Это значение также называется коэффициентом растяжения G. Его не следует смешивать с геометрической протяженностью сети, в которой помимо вершин учитываются также точки на ребрах.
Пусть дано конечное множество S точек на плоскости. Требуется найти плоскую геометрическую сеть G = (V, E) с насколько возможно малой протяженностью [math]\displaystyle{ \sigma(G) \; }[/math], такую, что S содержится в V. Значение
[math]\displaystyle{ \Sigma(S) := inf \{ \sigma(G); G = (V, E) \; }[/math] – конечная плоская геометрическая сеть, где [math]\displaystyle{ S \subset V \} \; }[/math]
называется протяженностью множества точек S. Задача заключается в вычислении или ограничении [math]\displaystyle{ \Sigma(S) \; }[/math] для данного множества S.
Родственные работы
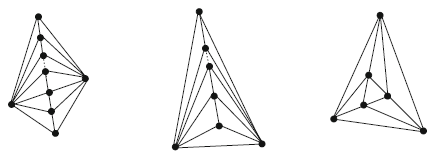
Если разрешены пересечения ребер, можно использовать остовы, протяженность которых может быть сделана произвольно близкой к 1; подробнее см. в монографиях Эпштейна [6] либо Нарасимхана и Смида [12]. Известны различные типы триангуляций S с коэффициентами растяжения, ограниченными сверху небольшими константами; среди них стоит упомянуть триангуляцию Делоне с коэффициентом растяжения, не превышающим 2,42; см. Добкин и др. [3], Кил и Гутвин [10], Дас и Джозеф [2]. Эпштейн [5] дал характеристику всех триангуляций T протяженностью [math]\displaystyle{ \sigma(T) = 1 \; }[/math]; эти триангуляции представлены на рис. 1. Очевидно, [math]\displaystyle{ \Sigma(S) = 1 \; }[/math] выполняется для любого множества точек S, содержащегося в множестве вершин подобной триангуляции T.
Рис. 1. Триангуляции протяженности 1
Основные результаты
Обращение предыдущего замечания также оказывается истинным.
Теорема 1 ([11]). Если множество S не содержится в одном из множеств вершин, изображенных на рис. 1, то [math]\displaystyle{ \Sigma(S) \gt 1 \; }[/math].
Иначе говоря, если множество точек S не является одним из этих специальных множеств, то любая плоская сеть, множество вершин которой включает S, имеет протяженность выше некоторой нижней границы [math]\displaystyle{ 1 + \eta(S) \; }[/math]. Доказательство теоремы 1 использует следующее соображение о плотности. Предположим, что каждая пара точек из S соединена отрезком прямой. Обозначим за S1 объединение S и всех получившихся точек пересечения. Применим то же самое построение к S1 и затем повторим процесс. Для множества предельных точек [math]\displaystyle{ S^\infty \; }[/math] верна следующая теорема. Она обобщает работы Хиллара и Ри [8], а также Исмаилеску и Радойчича [9], посвященные пересечениям линий.
Теорема 2 ([11]). Если множество S не содержится в одном из множеств вершин, изображенных на рис. 1, то [math]\displaystyle{ S^\infty \; }[/math] плотно располагается в некоторой многоугольной части плоскости.
Для определенных бесконечных структур могут быть доказаны конкретные нижние границы.
Теорема 3 ([4]). Пусть N – бесконечная плоская сеть, все грани которой имеют диаметр, ограниченный сверху некоторой константой. Тогда имеет место соотношение [math]\displaystyle{ \sigma(N) \gt 1,00156 \; }[/math].
Теорема 4 ([4]). Обозначим за C (бесконечное) множество всех точек на замкнутой выпуклой кривой. Тогда имеет место соотношение [math]\displaystyle{ \Sigma(C) \gt 1,00157 \; }[/math].
Теорема 5 ([4]). Пусть дано n семейств [math]\displaystyle{ F_i, 2 \le i \le n \; }[/math], каждое из которых состоит из бесконечного числа равноудаленных параллельных прямых. Предположим, что эти семейства находятся в общем положении. Тогда протяженность их графа пересечений G составляет не менее [math]\displaystyle{ 2 / \sqrt{3} \; }[/math].
Доказательство теоремы 5 основано на теореме Кронекера об одновременной аппроксимации. Граница достигается при помощи упаковки равноугольных треугольников.
Наконец, можно получить общую верхнюю границу протяженности конечных множеств точек.
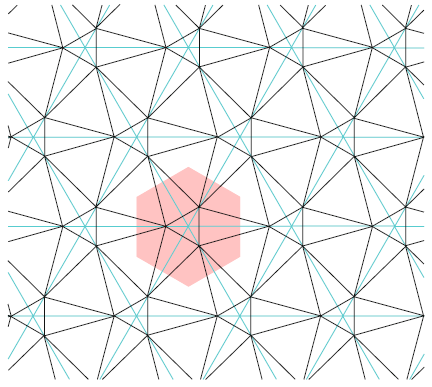
Теорема 6 ([4]). Каждое конечное множество точек S имеет протяженность [math]\displaystyle{ \Sigma(S) \lt 1,1247 \; }[/math].
Для доказательства этой верхней границы встроим любое заданное конечное множество точек S в множество вершин масштабированной и слегка деформированной конечной части сети, представленной на рис. 2. Ее можно получить из упаковки равносторонних треугольников в результате замены каждой вершины маленьким треугольником и соединения соседних треугольников указанным образом.
Рис. 2. Сеть протяженностью ~ 1,1247
Применение
Типичный университетский кампус включает такие места, как лекционные аудитории, общежития, библиотеки, клубы и супермаркеты, связанные некоторой системой путей. Торопящиеся студенты нередко сокращают путь через газоны, если выигрыш во времени кажется им достаточно убедительным. Со временем это приводит к возникновению новых путей. Поскольку их пересечения оказываются многолюдными, на них со временем появляются кофейни и другие новые заведения. Теперь студенты будут срезать дорогу по газонам на пути в кофейню, и так далее.
Д. Эпштейн [5] задался вопросом, что станет с газоном, если этот процесс будет продолжаться достаточно долго. Вышеприведенные результаты говорят о том, что, во-первых, часть газона будет полностью уничтожена и, во-вторых, искушение срезать дорогу через газон не может быть в общем случае сделано произвольно малым при помощи продуманной прокладки сети путей.
Открытые вопросы
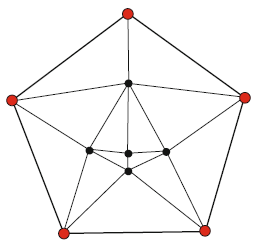
Для практического применения в дополнение к верхним границам протяженности пригодились бы верхние границы веса (т.е. общей длины ребер) геометрической сети. Некоторые теоретические вопросы также требуют дополнительного исследования. Всегда ли [math]\displaystyle{ \Sigma(S) \; }[/math] достигается для конечной сети? Как вычислить (точно или приближенно) [math]\displaystyle{ \Sigma(S) \; }[/math] для заданного конечного множества S? Даже для такого простого множества, как [math]\displaystyle{ S_5 \; }[/math], представляющего собой углы правильного пятиугольника, протяженность неизвестна. Наименьшее известное значение протяженности для триангуляции, среди вершин которой содержится [math]\displaystyle{ S_5 \; }[/math], равно 1,0204 (см. рис. 3). Наконец, чему равно точное значение [math]\displaystyle{ sup \{ \Sigma(S); S \; finite \} }[/math]?
Рис. 3. Наилучшее известное вложение для S5
См. также
Литература
1. Aronov, B., de Berg, M., Cheong, O., Gudmundsson, J., Haverkort, H., Vigneron, A.: Sparse Geometric Graphs with Small Dilation. 16th International Symposium ISAAC 2005, Sanya. In: Deng, X., Du, D. (eds.) Algorithms and Computation, Proceedings. LNCS, vol. 3827, pp. 50-59. Springer, Berlin (2005)
2. Das, G., Joseph, D.: Which Triangulations Approximate the Complete Graph? In: Proc. Int. Symp. Optimal Algorithms. LNCS 401, pp. 168-192. Springer, Berlin (1989)
3. Dobkin, D.P., Friedman, S.J., Supowit, K.J.: Delaunay Graphs Are Almost as Good as Complete Graphs. Discret. Comput. Geom. 5,399-407(1990)
4. Ebbers-Baumann, A., Gruene,A., Karpinski, M., Klein, R., Knauer, C., Lingas, A.: Embedding Point Sets into Plane Graphs of Small Dilation. Int. J. Comput. Geom. Appl. 17(3), 201-230 (2007)
5. Eppstein, D.: The Geometry Junkyard. http://www.ics.uci.edu/ ~eppstein/junkyard/dilation-free/
6. Eppstein, D.: Spanning Trees and Spanners. In: Sack, J.-R., Urrutia, J. (eds.) Handbook of Computational Geometry, pp. 425-461. Elsevier, Amsterdam (1999)
7. Eppstein, D., Wortman, K.A.: Minimum Dilation Stars. In: Proc. 21 st ACM Symp. Comp. Geom. (SoCG), Pisa, 2005, pp. 321-326
8. Hillar, C.J., Rhea, D.L A Result about the Density of Iterated Line Intersections. Comput. Geom.: Theory Appl. 33(3), 106-114(2006)
9. Ismailescu, D., Radoicic, R.: A Dense Planar Point Set from Iterated Line Intersections. Comput. Geom. Theory Appl. 27(3), 257-267 (2004)
10. Keil, J.M., Gutwin, C.A.: The Delaunay Triangulation Closely Approximates the Complete Euclidean Graph. Discret. Comput. Geom. 7,13-28(1992)
11. Klein, R., Kutz, M.: The Density of Iterated Plane Intersection Graphs and a Gap Result for Triangulations of Finite Point Sets. In: Proc. 22nd ACM Symp. Comp. Geom. (SoCG), Sedona (AZ), 2006, pp. 264-272
12. Narasimhan, G., Smid, M.: Geometric Spanner Networks. Cambridge University Press (2007)