Геометрические остовы

Ключевые слова и синонимы

Протяженность; t-остовы

Постановка задачи

Рассмотрим множество S из n точек в d-мерном Евклидовом пространстве. Сеть на множестве S может быть смоделирована при помощи неориентированного графа G с множеством вершин S размера n и множеством ребер E, в котором каждое ребро (г, м) имеет вес. Геометрическая (евклидова) сеть представляет собой сеть, в которой весом ребра (u, v) является евклидово расстояние |uv| между его конечными точками. Пусть дано вещественное число t > 1. Мы говорим, что граф G является t-остовом множества S, если для каждой пары точек [math]\displaystyle{ u, v \in S \; }[/math] существует путь в G, вес которого не более чем в t раз превышает евклидово расстояние между u и v. Минимальное значение t, при котором граф G является t-остовом S, называется коэффициентом растяжения, или протяженностью, G. Более детальное изложение процедуры построения t-остовов можно найти в книге Нарасимхана и Смида [18]. В данной статье рассматривается построение t-остовов для заданного множества S из n точек в пространстве [math]\displaystyle{ \mathcal{R}^d \; }[/math] и положительного вещественного числа t > 1, где d является константой.

Задача заключается в построении хорошего t-остова для S относительно следующих мер качества:

размер: количество ребер в графе;

степень: максимальное количество ребер, инцидентных вершине;

вес: сумма весов ребер;

диаметр остова: наименьшее целое число k, такое, что для любой пары вершин u и v из S существует путь в графе между u и v, длиной не более t • |uv| и содержащий не более k ребер;

отказоустойчивость: сохранение работоспособности графа при отказе ребра, вершины или области.

Таким образом, хорошие t-остовы должны иметь высокое значение отказоустойчивости и малые размер, степень, вес и диаметр.

Основные результаты

Далее будут изложены три самых распространенных подхода к построению t-остова на множестве точек в евклидовом пространстве, а также приведено описание процесса построения отказоустойчивых остовов и остовов в присутствии многоугольных препятствий; и, наконец, будут вкратце описаны динамические и кинетические остовы.

Остовы на точках в евклидовом пространстве

Максимально изученными классами t-остовных сетей для точек в евклидовом пространстве являются [math]\displaystyle{ \Theta \; }[/math]-графы, WSPD-графы и жадные остовы. В следующих разделах будут изложены базовые идеи, лежащие в основе каждого из этих классов, а также приведены известные границы мер качества.

[math]\displaystyle{ \Theta \; }[/math]-граф

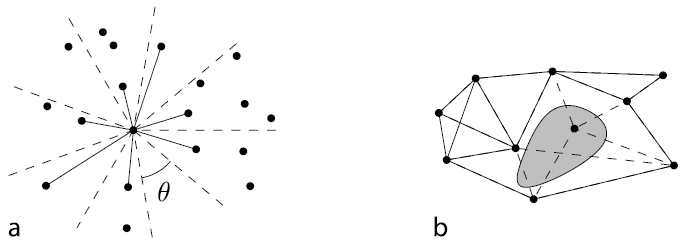
[math]\displaystyle{ \Theta \; }[/math]-графы были независимо разработаны в конце 80-х Кларксоном и Кейлом. Основная идея заключается в независимой обработке каждой точки [math]\displaystyle{ p \in S \; }[/math] следующим образом. Разобьем пространство [math]\displaystyle{ \mathcal{R}^d \; }[/math] на k симплициальных конусов с угловым диаметром не более [math]\displaystyle{ \theta \; }[/math] и вершиной в точке p, где [math]\displaystyle{ k = O(1 / \theta^{d - 1}) \; }[/math]. Для каждого непустого конуса C добавляется ребро, связывающее p и точку в C, ортогональная проекция которой на некоторый фиксированный луч в C, исходящий из p, является максимально близкой к p (см. рис. 1a). Полученный граф называется [math]\displaystyle{ \Theta \; }[/math]-графом на S.

Рисунок 1. a: [math]\displaystyle{ \Theta \; }[/math]-граф. b: граф с нерабочей областью

Теорема 1. [math]\displaystyle{ \Theta \; }[/math]-граф представляет собой t-остов на множестве S для [math]\displaystyle{ t = 1 / (cos \; \theta - sin \; \theta) }[/math], имеющий [math]\displaystyle{ O(n / \theta^{d - 1}) \; }[/math] ребер, и может быть вычислен за время [math]\displaystyle{ O((n / \theta^{d - 1}) log^{d - 1} \; n) }[/math] с использованием [math]\displaystyle{ O(n / \theta^{d - 1} + n \; log^{d - 2} \; n) }[/math] памяти.

Следующие варианты [math]\displaystyle{ \Theta \; }[/math]-графов задают границы на степень, диаметр и вес.

Остовы на базе списков с пропусками

Задача заключается в обобщении понятия списков с пропусками и применения их к построению остовов. Построим последовательность из h подмножеств, [math]\displaystyle{ S_1, ... S_h \; }[/math], где [math]\displaystyle{ S_1 = S \; }[/math], а [math]\displaystyle{ S_i \; }[/math] строится из [math]\displaystyle{ S_{i - 1} \; }[/math] следующим образом (напоминающим уровни в списке пропусков). Для каждой точки в [math]\displaystyle{ S_{i - 1} \; }[/math] подбросим симметричную монету. Множество [math]\displaystyle{ S_i \; }[/math] включает все точки [math]\displaystyle{ S_{i - 1} \; }[/math], для которых монета упала лицевой стороной вверх. Процесс построения заканчивается, когда [math]\displaystyle{ S_i = \empty \; }[/math]. Для каждого подмножества строится [math]\displaystyle{ \Theta \; }[/math]-граф. Объединение графов представляет собой остов S на базе списков с пропусками, имеющий протяженность t, [math]\displaystyle{ O(n / \theta^{d - 1}) \; }[/math] ребер и диаметр O(log n) с высокой вероятностью [3].

Жадный подход с пробелами

Множество ориентированных ребер удовлетворяет свойству пробелов, если источники любых двух разных ребер в множестве разделены расстоянием, по крайней мере в несколько раз превышающим длины кратчайшего из двух ребер. Арья и Смид [5] предложили алгоритм, использующий свойство пробелов для определения того, следует ли добавлять некоторое ребро к t-остовному графу. Используя свойство пробелов, можно доказать, что построенный остов имеет степень [math]\displaystyle{ O (1 / \theta^{d - 1}) \; }[/math] и вес O(log n • wt(MST(S))), где wt(MST(S)) – вес минимального остовного дерева S.

WSPD-граф

Пусть A и B – два конечных множества точек в [math]\displaystyle{ \mathcal{R}^d }[/math]. Будем называть A и B значительно удаленными по отношению к вещественному числу s > 0, если существуют два непересекающихся шара [math]\displaystyle{ C_A \; }[/math] и [math]\displaystyle{ C_B \; }[/math] одного и того же радиуса, такие, что [math]\displaystyle{ C_A \; }[/math] содержит A, [math]\displaystyle{ C_B \; }[/math] содержит B, а расстояние между [math]\displaystyle{ C_A \; }[/math] и [math]\displaystyle{ C_B \; }[/math] по меньшей мере в s раз превышает радиус [math]\displaystyle{ C_A \; }[/math]. Значение s называется коэффициентом удаления.

Определение 1 [6]. Пусть S – множество точек в пространстве [math]\displaystyle{ \mathcal{R}^d \; }[/math], а s > 0 – вещественное число. Декомпозицией значительно удаленных пар (well-separated pair decomposition, WSPD) для S относительно s является последовательность [math]\displaystyle{ \{ A_i, B_i \} , 1 \le i \le m \; }[/math], пар непустых подмножеств S, таких, что:

(1) [math]\displaystyle{ A_i \cap B_i = \empty \; }[/math] для всех i = 1, 2, ... , m;

(2) для каждой неориентированной пары {p, q} различных точек S существует ровно одна пара [math]\displaystyle{ \{ A_i, B_i \} \; }[/math] в последовательности, такая, что [math]\displaystyle{ p \in A_i \; }[/math] и [math]\displaystyle{ q \in B_i \; }[/math] либо [math]\displaystyle{ p \in B_i \; }[/math] и [math]\displaystyle{ q \in A_i \; }[/math];

(3) [math]\displaystyle{ A_i \; }[/math] и [math]\displaystyle{ B_i \; }[/math] являются значительно удаленными относительно s для всех i = 1, 2, ... , m.

Декомпозицию значительно удаленных пар разработали Кэллахан и Косарайю [6]. Построение t-остова при помощи этого подхода начинается с построения WSPD-декомпозиции S относительно коэффициента удаления s = (4(t + 1))/(t - 1). Вначале положим остовный граф равным [math]\displaystyle{ G = (S, \empty) \; }[/math] и будем итеративно добавлять ребра следующим образом. Для каждой значительно удаленной пары {A, B} из декомпозиции к графу добавляется ребро (a, b), где a и b – произвольные точки из A и B, соответственно. Полученный граф называется WSPD-графом на S.

Теорема 2. WSPD-граф представляет собой t-остов на множестве S, имеющий [math]\displaystyle{ O(s^d \cdot n) \; }[/math] ребер, и может быть построен за время [math]\displaystyle{ O(s^dn + n \; log \; n) }[/math], где s = 4(t + 1)/(t - 1).

В алгоритм можно внести модификации для получения графа с ограниченным диаметром или ограниченной степенью.

Граф с ограниченным диаметром

Арья, Маунт и Смид [3] предложили модификацию алгоритма построения, в результате которой диаметр графа оказывается ограничен 2 log n. Вместо выбора произвольной точки в каждом значительно удаленном множестве их алгоритм тщательно выбирает особую точку для каждого множества.

Граф с ограниченной степенью

Одна и та же точка v может быть частью нескольких значительно удаленных пар, и каждая из этих пар может сгенерировать ребро с конечной точкой в v. Арья и др. [2] предложили алгоритм, сохраняющий только самое короткое ребро для каждого направления конуса, объединив таким образом подход к построению [math]\displaystyle{ \Theta \; }[/math]-графа с подходом для WSPD-графа. Добавив шаг постобработки, рассматривающий все вершины с высокой степенью, можно получить t-остов степени [math]\displaystyle{ O(1 / (t - 1)^{2d - 1}) \; }[/math].

Жадный остов

Жадный алгоритм был впервые представлен в 1989 году Берном (см. также работу Ленкопулоса и Лингаса [15]) и с тех пор широко исследовался. Граф, построенный при помощи жадного алгоритма, будем называть жадным остовом. Основная идея заключается в итеративном построении графа G. Ребра полного графа обрабатываются в порядке возрастания длины. Проверка ребра (u, v) включает запрос о кратчайшем пути в частичном остовном графе G. Если кратчайший путь в G между u и v не превышает t • |uv|, то ребро (u, v) отбрасывается, в противном случае оно добавляется к частичному остовному графу G.

Дас, Нарасимхан и Салоу [11] доказали, что жадный остов удовлетворяет так называемому свойству прыжков. Множество неориентированных ребер E удовлетворяет свойству t-прыжков, если для любого [math]\displaystyle{ k \ge 2 \; }[/math] и любой возможной последовательности [math]\displaystyle{ \{ (p_1, q_1), ..., (p_k, q_k) \} \; }[/math] попарно различающихся ребер E выполняется соотношение

[math]\displaystyle{ t \cdot |p_1 q_1| \lt \sum^k_{i = 2} |p_i q_i| + t \cdot \Big( \sum^{k - 1}_{i = 1} |q_i p_{i + 1}| + |p_k q_1| \Big) }[/math].

Используя свойство прыжков, можно ограничить вес графа. Дас и Нарасимхан [10] заметили, что жадный остов можно вычислить приближенно при удовлетворении свойства прыжков. Это наблюдение позволило разработать более быстрые алгоритмы для его построения.

Теорема 3 ([14]). Приближенный жадный t-остов на множестве S, имеющий максимальную степень [math]\displaystyle{ O(1/(t - 1)^{2d - 1}) \; }[/math] и вес [math]\displaystyle{ O((1 / (t - 1)^{2d - 1} \cdot wt(MST(S)))) }[/math], может быть построен за время [math]\displaystyle{ O(n/((t - 1)^{2d}) \; log \; n) }[/math].

Отказоустойчивые остовы

Понятие отказоустойчивых остовов было введено Левкопулосом и др. [16] в 1998 году. Оно означает, что при отказе одной или нескольких вершин либо одного или нескольких ребер остов должен сохранить свои основные свойства. В частности, в том, что осталось от остова после отказа вершин или ребер, по-прежнему должен сохраниться короткий путь между любыми двумя вершинами. Шумай и Чжао [8] показали, что жадный подход позволяет получить k-вершинный (или k-реберный) отказоустойчивый геометрический t-остов степени O(k) с общим весом [math]\displaystyle{ O(k^2 \cdot wt(MST(S))) \; }[/math]; эти границы являются асимптотически оптимальными.

Для геометрических остовов естественно рассматривать отказы областей – то есть отказы, уничтожающие все вершины и ребра, пересекающие некоторую нерабочую геометрическую область. Пусть для нерабочей области F граф [math]\displaystyle{ G \ominus F }[/math] представляет собой часть G, оставшуюся после того, как точки из S, находящиеся внутри области F, и все ребра, пересекающие F, были удалены из графа; см. рис. 1b. Абам и др. [1] показали, как строить t-остовы размера O(n log n), являющиеся отказоустойчивыми при отказе любой выпуклой области. Если разрешается использовать точки Штейнера, можно получить t-остов линейного размера.

Остовы с многоугольными препятствиями

Граф видимости на множестве попарно непересекающихся многоугольников называется графом взаимовидимых областей. Каждая многоугольная вершина является вершиной в графе, а каждое ребро представляет видимую связь между ними: если две вершины видят друг друга, между ними строится ребро. Этот граф полезен благодаря тому, что содержит кратчайший путь, огибающий препятствия, между парой любых вершин.

Дас [9] показал, что t-остов графа видимости для множества точек на евклидовой плоскости можно получить при помощи алгоритма построения [math]\displaystyle{ \Theta \; }[/math]-графа с последующим этапом усечения. Полученный граф будет иметь линейный размер и константную степень.

Динамические и кинетические остовы

О динамических или кинетических остовах известно не так уж много. Арья и др. [4] предложили структуру данных размера O(n log n), поддерживающую остов на базе списков с пропусками, описанный выше, с ожидаемым амортизированным временем вставки и удаления [math]\displaystyle{ O(log^d \; n \; log \; log \; n) }[/math] на основе модели случайных обновлений.

Гао и др. [13] показали, как поддерживать t-остов размера [math]\displaystyle{ O(n/(t - 1)^d) \; }[/math] с максимальной степенью [math]\displaystyle{ O(1 / (t - 2)^d \; log \; \alpha) }[/math] и временем вставки и удаления [math]\displaystyle{ O((log \; \alpha)/(t - 1)^d) }[/math], где [math]\displaystyle{ \alpha \; }[/math] обозначает пропорциональность S, т.е. отношение максимального расстояния между парой вершин к минимальному. Алгоритм основан на использовании иерархической структуры T с [math]\displaystyle{ O(log \; \alpha) }[/math] уровнями, каждый уровень которой содержит множество центров (подмножество S). Каждая вершина v на уровне i в структуре T связана ребрами со всеми остальными вершинами уровня i, находящимися на расстоянии не более [math]\displaystyle{ O(2^i / (t - 1)) \; }[/math] от v. Полученный граф является t-остовом S и может поддерживаться вышеописанным образом. Этот подход может быть обобщен до кинетического случая таким образом, чтобы количество событий в процессе поддержки остова составляло [math]\displaystyle{ O(n^2 \; log \; n) }[/math] при псевдоалгебраическом характере перемещения. Каждое событие может быть обновлено за время [math]\displaystyle{ O((log \; \alpha)/(t - 1)^d) }[/math].

Применение

Алгоритмы построения разреженных остовов получили широкое применение в таких областях, как поиск в метрическом пространстве [1], который включает запрос по содержанию в мультимедийных объектах, текстовый информационный поиск, распознавание образов и аппроксимацию функций. Еще одним примером является широковещательная рассылка в сетях коммуникаций [17]. Несколько хорошо известных теоретических работ также основываются на построении t-остовов – к примеру, Рао и Смит [19] совершили прорыв, предложив схему аппроксимации с оптимальным временем O(nlog n) для хорошо известной евклидовой задачи коммивояжера с использованием t-остовов (или баньянов). А Шумай и Лингас [7] предложили схемы аппроксимации для задач о многосвязности с нахождением объектов минимальной стоимости в геометрических сетях.

Открытые вопросы

В этой сфере остается много нерешенных задач. Стоит упомянуть некоторые из них:

1. Разработка алгоритма построения динамического t-остова, который можно обновлять за время [math]\displaystyle{ O(log^c \; n) }[/math] для некоторого константного значения c.

2. Определение, существует ли отказоустойчивый t-остов линейного размера для ситуации отказов выпуклых областей.

3. Алгоритм построения k-вершинного отказоустойчивого остова, который предложили Шумай и Чжао [8], позволяет получить k-вершинный отказоустойчивый t-остов степени O(k) с общим весом [math]\displaystyle{ O(k^2 \cdot wt(MST(S))) \; }[/math]. Однако до сих пор неизвестны способы его эффективной реализации. Можно ли вычислить такой остов за время O(n log n + kn)?

4. Ограничение веса остовов на базе списков с пропусками.

Экспериментальные результаты

Задача построения остовов активно исследовалась с теоретической точки зрения, но получила гораздо меньше внимания с практической, или экспериментальной, стороны. Наварро и Паредес [1] предложили четыре эвристики для множеств точек в пространстве высоких размерностей (d = 20) и эмпирическими методами показали, что время выполнения составило [math]\displaystyle{ O(n^{2,24}) \; }[/math], а количество ребер в полученных графах – [math]\displaystyle{ O(n^{1,13}) \; }[/math]. Недавно Фарши и Гудмундссон [12] провели тщательное сравнение алгоритмов построения остовов, упоминавшихся в разделе «Остовы на точках в евклидовом пространстве».

См. также

• Применение геометрических остовных сетей
• Аппроксимация метрических пространств древесными метриками
• Протяженность геометрических сетей
• Планарные геометрические остовы
• Алгоритм поиска кратчайших путей с единственным источником
• Разреженные остовы графов
• Декомпозиция значительно удаленных пар

Литература

1. Abam, M.A., de Berg, M., Farshi, M., Gudmundsson, J.: Region-fault tolerant geometric spanners. In: Proceedings of the 18th ACM-SIAM Symposium on Discrete Algorithms, New Orleans, 7-9 January 2007

2. Arya, S., Das, G., Mount, D.M., Salowe, J.S., Smid, M.: Euclidean spanners: short, thin, and lanky. In: Proceedings of the 27th ACM Symposium on Theory of Computing, pp. 489-498. Las Vegas, 29 May-1 June 1995

3. Arya, S., Mount, D.M., Smid, M.: Randomized and deterministic algorithms for geometric spanners of small diameter. In: Proceedings of the 35th IEEE Symposium on Foundations of Computer Science, pp. 703-712. Santa Fe, 20-22 November 1994

4. Arya, S., Mount, D.M., Smid, M.: Dynamic algorithms for geometric spanners of small diameter: Randomized solutions. Comput. Geom. Theor. Appl. 13(2), 91 -107 (1999)

5. Arya, S., Smid, M.: Efficient construction of a bounded-degree spanner with low weight. Algorithmica 17, 33-54 (1997)

6. Callahan, P.B., Kosaraju, S.R.: A decomposition of multidimensional point sets with applications to k-nearest-neighbors and n-body potential fields. J. ACM 42,67-90 (1995)

7. Czumaj, A., Lingas, A.: Fast approximation schemes for Euclidean multi-connectivity problems. In: Proceedings of the 27th International Colloquium on Automata, Languages and Programming. Lect. Notes Comput. Sci. 1853,856-868 (2000)

8. Czumaj, A., Zhao, H.: Fault-tolerant geometric spanners. Discret. Comput. Geom. 32(2), 207-230 (2004)

9. Das, G.: The visibility graph contains a bounded-degree spanner. In: Proceedings of the 9th Canadian Conference on Computational Geometry, Kingston, 11-14 August 1997

10. Das, G., Narasimhan, G.: A fast algorithm for constructing sparse Euclidean spanners. Int. J. Comput. Geom. Appl. 7,297-315(1997)

11. Das, G., Narasimhan, G., Salowe, J.: A new way to weigh malnourished Euclidean graphs. In: Proceedings of the 6th ACM-SIAM Symposium on Discrete Algorithms, pp. 215-222. San Francisco, 22-24 January 1995

12. Farshi, M., Gudmundsson, J.: Experimental study of geometric t-spanners. In: Proceedings of the 13th Annual European Symposium on Algorithms. Lect. Notes Comput. Sci. 3669, 556-567 (2005)

13. Gao, J., Guibas, L.J., Nguyen, A.: Deformable spanners and applications. In: Proceedings of the 20th ACM Symposium on Computational Geometry, pp. 190-199, New York, 9-11 June 2004

14. Gudmundsson, J., Levcopoulos, C., Narasimhan, G.: Improved greedy algorithms for constructing sparse geometric spanners. SIAM J. Comput. 31(5), 1479-1500 (2002)

15. Levcopoulos, C., Lingas, A.: There are planar graphs almost as good as the complete graphs and almost as cheap as minimum spanning trees. Algorithmica 8(3), 251-256 (1992)

16. Levcopoulos, C., Narasimhan, G., Smid, M.: Improved algorithms for constructing fault-tolerant spanners. Algorithmica 32, 144-156(2002)

17. Li, X.Y.: Applications of computational geometry in wireless ad hoc networks. In: Cheng, X.Z., Huang, X., Du, D.Z. (eds.) Ad Hoc Wireless Networking, pp. 197-264. Kluwer, Dordrecht (2003)

18. Narasimhan, G., Smid, M.: Geometric spanner networks. Cambridge University Press, New York (2006)

19. Navarro, G., Paredes, R.: Practical construction of metric t-spanners. In: Proceedings of the 5th Workshop on Algorithm Engineering and Experiments, pp. 69-81, 11 January 2003. SIAM Press, Baltimore

20. Rao, S., Smith, W.D.: Approximating geometrical graphs via spanners and banyans. In: Proceedings of the 30th ACM Symposium on Theory of Computing, pp. 540-550. Dallas, 23-26 May 1998