Остовное дерево с максимальным количеством листьев

Ключевые слова и синонимы

Связное доминирующее множество; экстремальная структура

Постановка задачи

Задача построения остовного дерева с максимальным количеством листьев (ОДМЛ; MAX LEAF SPANNING TREE) заключается в нахождении остовного дерева, имеющего не менее k листьев, на неориентированном графе. Версия разрешимости для параметризованной задачи построения ОДМЛ выглядит следующим образом:

Дано: связный граф G, целое число k.

Параметр: целое число k.

Вопрос: имеет ли граф G с не менее чем k листьями?

Параметризованная сложность недетерминированного полного алгоритма ОДМЛ с полиномиальным временем выполнения широко изучалась [2, 3, 9, 11] с использованием кернелизации, ветвления и других техник с фиксированными параметрами (fixed-parameter tractable, FPT). Авторы работы [8] первыми предложили метод на базе экстремальной структуры для решения сложных вычислительных задач. Этот метод, напоминающий подход Гротендика и по духу сходный с проектом миноров графов Робертсона и Сеймура, заключается в том, что математический развивается как серия небольших шагов, выполняемых по общей траектории, описываемой подходящей «математической машиной». Авторы подхода предпочитают высказывания следующего типа: Каждый связный граф с n вершинами, удовлетворяющий определенному набору свойств, имеет остовное дерево с не менее чем k листьями, и это остовное дерево можно найти за время O(f(k) + nc), где c – константа (независимая от k), а / - произвольная функция.

При рассмотрении параметризованной сложности значение k называется параметром, который в определенном смысле отражает структуру входных данных или другой аспект цели вычисления. Например, k может обозначать количество ребер, которые необходимо удалить для получения графа без циклов; количество последовательностей ДНК, подлежащих выравниванию в задаче выравнивания последовательностей; максимальную глубину вложенности объявления типа у компилятора; k = 1/e может обозначать параметризацию при анализе аппроксимации; кроме того, k также может быть составным значением, зависящим от нескольких переменных.

Существуют два основных способа сравнения FPT-алгоритмов, в результате чего появилось два класса FPT-задач. В классе «f(k)» задача заключается в поиске еще более медленно растущих функций от параметра f(k), управляющих сложностью FPT-алгоритмов. Класс «кернелизации» опирается на следующую лемму, утверждающую, что задача принадлежит к разряду FPT-задач в том и только том случае, если входные данные могут быть предварительно обработаны (кернелизованы) за «обычное» полиномиальное время с получением экземпляра, размер которого ограничивается только функцией от k.

Лемма 1. Параметризованная задача П является задачей с фиксированными параметрами (FPT) в том и только том случае, если существует преобразование с полиномиальным временем выполнения (относительно n и k), переводящее (x, k) в (x0; k0), такое, что:

(1) (x, k) является «да-экземпляром» TI в том и только том случае, если (x0; k0) является «да-экземпляром» П,

(2) k0 < k,

(3) \x'\ < g(k) для некоторой фиксированной функции g.

В ситуации, описываемой леммой, можно сказать, что мы можем кернелизовать исходные экземпляры до экземпляров размером не более g(k). Два этих класса задач нередко бывают тесно связаны, однако результаты их выполнения различаются. Наилучший известный FPT-алгоритм задачи построения остовного дерева с максимальным количеством листьев с временем выполнения O*(8.12) предложил Бонсма [ ] на основе подхода на базе экстремальных структур, который разработали Эстивилл-Кастро, Феллоуз, Лэнгстон и Розамонд [8]. Этот алгоритм определяет, имеет ли граф G с n вершинами остовное дерево не менее чем с k листьями. В то же время авторы работы [8] представили FPT-алгоритм с наименьшим размером ядра.

Можно выделить пять независимых объектов, связанных с теорией экстремальных структур и иллюстрирующих все цели алгоритма построения остовного дерева с максимальным количеством листьев. Перечислим эти пять целей:

(а) Более эффективные FPT-алгоритмы, полученные в результате применения теории более глубокой структуры, более мощных правил редукции, связанных с этой теорией, и более сильных доказательств по индукции для улучшенных границ кернелизации.

(б) Правила мощной предварительной обработки (редукции данных / кернелизации) и комбинации правил, которые могут использоваться независимо от того, насколько мал параметр, и могут комбинироваться с другими подходами – например, аппроксимацией и эвристиками. Обычно они несложны для программирования.

(в) Градиенты и правила преобразования для эвристик локального поиска.

(г) Алгоритмы аппроксимации с полиномиальным временем выполнения и границы эффективности, доказанные систематическим образом.

(д) Структура, используемая для решения других задач.

Основные результаты

Основным результатом является метод использования экстремальной структуры в качестве системного подхода к разработке FPT-алгоритмов. Рассмотрим пять перечисленных выше взаимосвязанных целей, проиллюстрировав каждую при помощи данной задачи.

Цель (а): FPT-алгоритмы

Задача заключается в нахождении правил предварительной обработки (кернелизации) с полиномиальным временем выполнения, где g(k) насколько возможно мало. Это будет важно впоследствии в контексте цели (б).

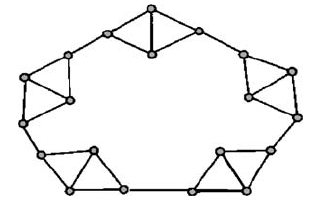
Рис. 1. Правила редукции были выведены для редукции данной структуры графа Клейтмана-Веста

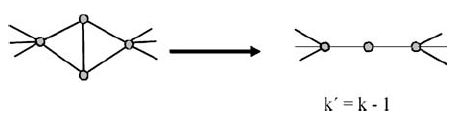
Если перефразировать задачу в терминах структурной теории, важнейший вопрос будет звучать следующим образом: какова структура графов, не имеющих подграфа с k листьями? Результат Клейтмана и Веста из теории графов показывает, что граф с минимальной степенью не менее 3, не включающий подграф с k листьями, имеет не более 4(k - 3) вершин. На рис. 1 показано, что это лучший возможный результат для данной гипотезы. Однако исследование структуры при помощи экстремальных методов выявляет необходимость в применении правила редукции, показанного на рис. 2. Примерно 20 различных правил редукции с полиномиальным временем выполнения (некоторые из них являются намного более сложными и «глобальными» по своей структуре, чем приведенное для примера простое локальное правило редукции) будет достаточно для кернелизации графа с минимальной степенью 2, имеющего не более 3,5k вершин.

Рис. 2. Правило редукции для графа Клейтмана-Веста

В общем случае экземпляр параметризованной задачи состоит из пары (x, k) и «границы», которая вычисляется посредством фиксации x и изменения k с последующим определением, какой ответ имеет задача разрешимости – «да» или «нет. Представляет интерес величина границы при редукции x. Типичная граничная лемма выглядит следующим образом.

Лемма 2. Пусть (G, k) – экземпляр задачи построения остовного дерева с максимальным количеством листьев после редукции, для которого (G, k) является «да-экземпляром», а (G, k + 1) – «нет-экземпляром». Тогда |G| < ck (где c – небольшая константа, значение которой будет вычислено в результате решения).

Доказательство граничной леммы выполняется при помощи минимального контрпримера. Контрпримером будет служить граф, такой, что (1) (G, k) – экземпляр задачи ОДМЛ после редукции; (2) (G, k) является «да-экземпляром»; (3) (G, k + 1) является «нет-экземпляром»; (4) |G| < ck.

Доказательство граничной леммы будет производиться последовательным образом. Изначально неизвестно, при каком значении границы будет достигнут успех, а также точно неизвестно, что подразумевается под редукцией. В ходе доказательства эти аспекты станут ясны. По мере раскрытия аргументов особенности структуры подскажут формулировки новых правил редукции. При доказательстве граничной леммы необходимо будет принимать следующие стратегические решения:

(1) Определение полярности границы и формулировка граничной леммы.

(2) Выбор структуры-свидетеля.

(3) Задание индуктивных приоритетов.

(4) Разработка серии утверждений по поводу структуры, описывающих ситуацию на границе.

(5) Определение правил редукции, выполняющихся за полиномиальное время над релевантными компонентами структуры на границе.

(6) По мере уточнения структуры на границе – заполнение неизвестных компонентов границы кернелизации.

Общая структура аргумента вычисляется при помощи минимального контрпримера согласно приоритетам, заданным в результате выбора (3), который обычно ссылается на выбор (2). Доказательство развивается посредством серии небольших шагов, состоящих из серии утверждений по поводу структуры, которые в сумме ведут к получению детальной картины представления структур на «границе» и, следовательно, позволяют определить границу размера G, на основе которой выводится заключение леммы. Полное доказательство объединяет серию утверждений по поводу дерева-свидетеля, различных множеств вершин и индуктивных приоритетов индукции и формулирует основное неравенство, на основе которого производится доказательство по индукции, и ядро задачи размера 3,5k.

Цель (б): предварительная обработка с полиномиальным временем выполнения и подпрограммы редукции данных

Ниже приводится пример таблицы, используемой для отслеживания каждого возможного состояния границы для возможного решения. Можно привести примеры, демонстрирующие исключительно успешное каскадное применение правил редукции данных к реальным распределениям данных и описывающие разнообразие математических феноменов, относящихся к правилам редукции. Например, некоторые правила редукции – такие как правило разложения на составляющие Клейтмана-Веста для задачи ОДМЛ (рис. 2) – имеют фиксированный «размер границы» (в данном случае равный 2), тогда как правила редукции типа «корона» не имеют такового.

Цель (в): градиенты и преобразования решений для локального поиска

Здесь производится обобщение обычной формулировки для локального поиска, основанное на степени более сложного градиента в процессе получения более высоких границ кернелизации. Первая идея заключается в проведении локального поиска на основе поддержки «текущей структуры-свидетеля», а не полного решения (остовного дерева). Вторая идея состоит в использовании списка индуктивных приоритетов для определения градиента «лучшего решения» для локального поиска.

Цель (г): алгоритмы аппроксимации с полиномиальным временем выполнения

Теория использования экстремальных структур с полиномиальным временем выполнения напрямую приводит к получению алгоритма аппроксимации ОДМЛ с константным множителем и полиномиальным временем выполнения. Вначале выполним редукцию G при помощи правил кернелизации. Правила редукции сохраняют параметры аппроксимации. Возьмем любое дерево T (не обязательно остовное) в G. Если выполняются все утверждения касательно структуры, тогда (согласно рассуждениям граничной леммы) дерево T должно иметь не менее n/c листьев для c = 3,75. Таким образом, восстановив T с учетом произведенной редукции, получим c-аппроксимацию.

Если по меньшей мере одно утверждение касательно структуры не выполняется, то дерево T можно улучшить, опираясь на один из индуктивных приоритетов. Заметим, что каждое утверждение доказано посредством рассуждения, которое можно интерпретировать как подпрограмму улучшения T с полиномиальным временем выполнения в случае противоречия утверждению.

Последовательность этих действий можно применить к исходному дереву T (и его потомкам) только полиномиальное количество раз, определяемое списком индуктивных приоритетов, до того момента, как мы получим дерево V, для которого выполняются все утверждения касательно структуры. В этот момент мы должны получить решение с c-аппроксимацией.

Цель (г): структура, используемая для определения экологии сложности

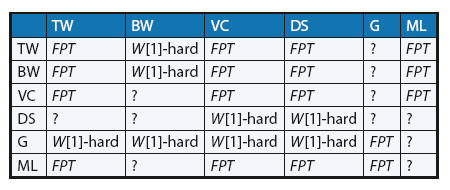
Цель заключается в том, чтобы понять, как именно каждый параметр, определяющий входные данные задачи, влияет на сложность всех других задач. В качестве примера рассмотрим таблицу 1:

Таблица 1. Экология сложности параметров