Обмен ближайшими соседями и относительные расстояния
Ключевые слова и синонимы
Сравнение филогенетических деревьев; сетевые модели эволюции
Постановка задачи
В данном обзоре будут рассмотрены результаты исследований расстояния на базе преобразований для эволюционных деревьев. В различных публикациях было предложено несколько моделей измерения расстояний для эволюционных деревьев. Самой известной из них, вероятно, можно считать модель расстояния обмена ближайшими соседями (nearest neighbor interchange, nni), независимо введенную в [10] и [9]. Помимо расстояния nni, стоит также обратить внимание на родственное понятие, называемое расстоянием переноса поддеревьев и введенное в [5, 6]. Несколько работ, авторами которых были Дасгупта, Хе, Цзян, Ли, Тромп и Чжан, продемонстрировали следующие результаты:
• найдено соответствие между расстоянием обмена ближайшими соседями и расстоянием переноса поддеревьев с линейной стоимостью на невзвешенных деревьях;
• вычисление расстояния обмена ближайшими соседями является NP-полной задачей, однако допускает возможность разрешимости с фиксированными параметрами и применение алгоритмов аппроксимации с логарифмическим коэффициентом;
• разработан алгоритм 2-аппроксимации для вычисления расстояния переноса поддеревьев с линейной стоимостью на взвешенных эволюционных деревьях.
Вначале определим расстояние обмена ближайшими соседями и расстояние переноса поддеревьев с линейной стоимостью для невзвешенных деревьев; затем расширим эти понятия на взвешенные деревья. Далее будет считаться, что эволюционное (или филогенетическое) дерево является неупорядоченным, имеет листья с уникальными метками и непомеченные внутренние вершины, может быть корневым или некорневым, взвешенным или невзвешенным, а все внутренние вершины имеют степень 3.
Невзвешенные деревья
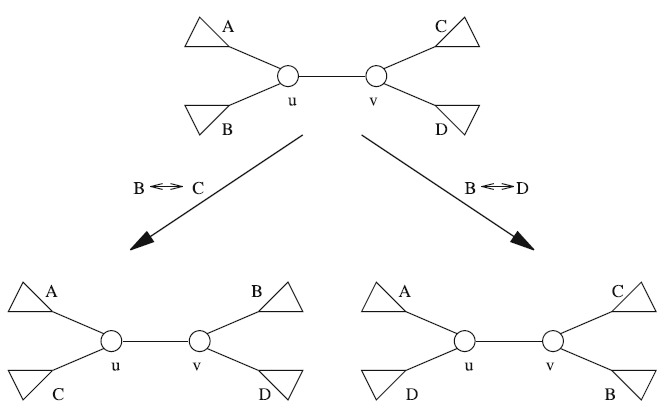
Операция обмена ближайшими соседями (nni) обменивает два поддерева, разделенных внутренним ребром (u, v), как показано на рис. 1.
Считается, что операция nni действует на это внутреннее ребро. Расстояние обмена ближайшими соседями, [math]\displaystyle{ D_{nni}(T_1, T_2) \; }[/math], между двумя деревьями [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] определяется как минимальное число операций nni, необходимое для преобразования одного дерева в другое.
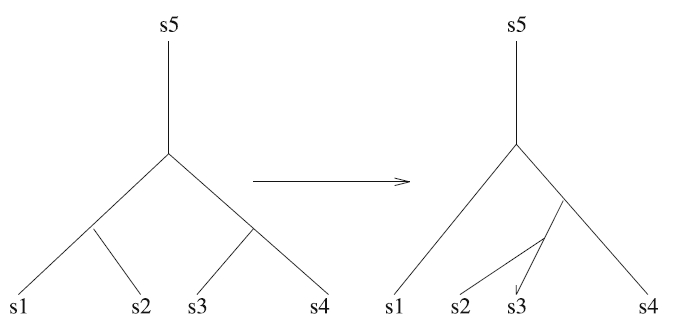
Операцию обмена ближайшими соседями также можно рассматривать как перемещение поддерева за соседнюю внутреннюю вершину. Более общая операция перемещает поддерево из одной точки дерева в другую произвольную точку. На рис. 2 представлена такая операция переноса поддерева.
Рис. 1. Две возможных операции обмена ближайшими соседями на внутреннем ребре (u,v): обмен [math]\displaystyle{ B \leftrightarrow C \; }[/math] или [math]\displaystyle{ B \leftrightarrow D \; }[/math]
Расстояние переноса поддеревьев между двумя деревьями [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] определяется как минимальное количество поддеревьев, необходимое для преобразования [math]\displaystyle{ T_1 \; }[/math] в [math]\displaystyle{ T_2 \; }[/math] [5, 6, 7]. Иногда на практике бывает необходимо проводить различие между разными операциями переноса поддеревьев, поскольку они встречаются с разной частотой. В таком случае можно назначить каждой операции переноса поддерева стоимость, равную расстоянию (в числе пройденных вершин), на которое поддерево перенесено в текущем дереве. Расстояние переноса поддеревьев с линейной стоимостью, [math]\displaystyle{ D_{lcst}(T_1, T_2) \; }[/math], между двумя деревьями [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] определяется как минимальная стоимость, затрачиваемая на преобразование [math]\displaystyle{ T_1 \; }[/math] в [math]\displaystyle{ T_2 \; }[/math] при помощи операций переноса поддеревьев [1, 2].
Рис. 2. Пример переноса одного поддерева
Взвешенные деревья
Модели обмена ближайшими соседями и переноса поддеревьев с линейной стоимостью можно естественным образом расширить на взвешенные деревья. В первом случае расширение выполнить несложно: операции nni просто присваивается стоимость, равная весу ребра, над которым она производится. Чтобы обмен ближайшими соседями между взвешенными деревьями [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] был осуществимым, необходимо, чтобы выполнялись следующие условия: (1) для каждой метки листа a вес ребра в [math]\displaystyle{ T_1 \; }[/math], инцидентного a, равен весу ребра в [math]\displaystyle{ T_2 \; }[/math], инцидентного a; (2) мультимножества весов внутренних ребер [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] совпадают.
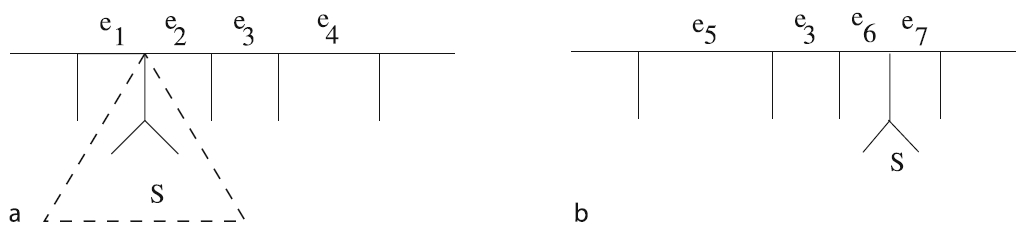
В случае переноса поддеревьев с линейной стоимостью кажется логичным, чтобы за перемещение поддерева взималась «плата» в соответствии с пройденным им расстоянием, однако стоит дать более формальное определение. Рассмотрим (некорневые) деревья, в которых каждому ребру [math]\displaystyle{ e \; }[/math] приписан вес [math]\displaystyle{ w(e) \ge 0 \; }[/math]. Для того чтобы одно дерево можно было преобразовать в другое, необходимо, чтобы полный вес всех ребер был равен единице. Теперь перенос поддеревьев можно определить следующим образом. Выберите поддерево S дерева T в заданной вершине u, выберите ребро [math]\displaystyle{ e \notin S \; }[/math]. Расщепите ребро [math]\displaystyle{ e \; }[/math] на два ребра [math]\displaystyle{ e_1 \; }[/math] и [math]\displaystyle{ e_2 \; }[/math] с весами [math]\displaystyle{ w(e_1) \; }[/math] и [math]\displaystyle{ w(e_2) \; }[/math] [math]\displaystyle{ (w(e_1), w(e_2) \ge 0,w(e_1) + w(e_2) = w(e)) }[/math], и переместите S в общую конечную точку [math]\displaystyle{ e_1 \; }[/math] и [math]\displaystyle{ e_2 \; }[/math]. После этого выполните слияние двух оставшихся ребер e' и e, смежных с u, в одно ребро с весом w(e') + w(e). Стоимость этого переноса поддеревьев представляет собой сумму весов всех ребер, через которые перемещается S. Пример переноса приведен на рис. 1. Веса ребер исходного дерева нормализованы, чтобы их общая сумма была равна 1. Поддерево S переносится таким образом, что ребро [math]\displaystyle{ e_4 \; }[/math] разбивается на [math]\displaystyle{ e_6 \; }[/math] и [math]\displaystyle{ e_7 \; }[/math], при этом [math]\displaystyle{ w(e_6), w(e_7) \ge 0 \; }[/math] и [math]\displaystyle{ w(e_6) + w(e_7) = w(e_4) \; }[/math] наконец, два ребра [math]\displaystyle{ e_1 \; }[/math] и [math]\displaystyle{ e_2 \; }[/math] сливаются вместе, образуя ребро [math]\displaystyle{ e_5 \; }[/math], такое, что [math]\displaystyle{ w(e_5) = w(e_1) + w(e_2) \; }[/math]. Стоимость переноса S составит [math]\displaystyle{ w(e_2) + w(e_3) + w(e_6) \; }[/math].
Заметим, что для взвешенных деревьев модель переноса поддеревьев с линейной стоимостью является более общей, чем модель обмена ближайшими соседями – в том смысле, что поддерево можно переносить вдоль ребра при помощи первой модели, тогда как в рамках второй этого не удастся сделать.
Рис. 3. Перенос поддеревьев на взвешенных филогенетических деревьях. Дерево b получается из дерева a при помощи одного переноса поддерева
Основные результаты
Пусть [math]\displaystyle{ T_1 \; }[/math] и T2 – два дерева, каждое из которых содержит n вершин, используемых при вычислении расстояния.
Теорема 1 ([2, 3, 4]). Предположим, что деревья [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] невзвешенные. Тогда верны следующие утверждения:
• [math]\displaystyle{ D_{nni}(T_1, T_2) = D_{lcst}(T_1, T_2) \; }[/math].
• Вычисление [math]\displaystyle{ D_{nni} (T_1, T_2) \; }[/math] представляет собой NP-полную задачу.
• Предположим, что [math]\displaystyle{ D_{nni}(T_1, T_2) \lt d \; }[/math]. Тогда оптимальная последовательность операций обмена ближайшими соседями, преобразующая [math]\displaystyle{ T_1 \; }[/math] в [math]\displaystyle{ T_2 \; }[/math], может быть вычислена за время [math]\displaystyle{ O(n^2 log \; n + n \cdot 2^{23d/2}) }[/math].
• Значение [math]\displaystyle{ D_{nni}(T_1, T_2) \; }[/math] может быть приближенно вычислено с коэффициентом аппроксимации [math]\displaystyle{ log \; n + O(1) }[/math] за полиномиальное время.
Теорема 2 ([1, 2, 3, 4]). Предположим, что деревья [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] взвешенные. Тогда верны следующие утверждения:
• Значение [math]\displaystyle{ D_{nni}(T_1, T_2) \; }[/math] может быть приближенно вычислено с коэффициентом аппроксимации [math]\displaystyle{ 6 + 6 log \; n }[/math] за время [math]\displaystyle{ O(n^2 log \; n) }[/math].
• Предположим, что [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] могут иметь листья с неуникальными метками. Тогда вычисление [math]\displaystyle{ D_{lcst}(T_1, T_2) \; }[/math] представляет собой NP-полную задачу.
• Значение [math]\displaystyle{ D_{lcst} (T_1, T_2) \; }[/math] может быть приближенно вычислено с коэффициентом аппроксимации 2 за время [math]\displaystyle{ O(n^2 log \; n) }[/math].
Применение
Здесь рассматриваются результаты, касающиеся связанных с преобразованиями расстояний для эволюционных деревьев. Такие деревья могут быть корневыми, если известно эволюционное происхождение, а также взвешенными, если известна продолжительность эволюции по каждому ребру. Реконструкция корректного эволюционного дерева для множества видов является одной из фундаментальных, и при этом весьма сложных, проблем эволюционной генетики. За последние десятилетия было разработано несколько подходов к реконструкции эволюционных деревьев, основанных на таких критериях, как максимальные экономичность, совместимость, расстояние и правдоподобие. Результаты применения этих подходов обычно зависят от объема данных и вычислительных ресурсов, использовавшихся в расчетах. В результате на практике из одних и тех же множеств видов нередко получаются разные эволюционные деревья [8]. Таким образом, представляет интерес возможность сравнения эволюционных деревьев, полученных при помощи разных методов либо при помощи одного и того же метода, но на разных данных.
Еще одна мотивация для исследований в области вычисления расстояния переноса поддеревьев с линейной стоимостью заключается в следующем. Когда в процессе эволюции происходит рекомбинация ДНК, две последовательности встречаются и генерируют новую последовательность, состоящую из генетического материала, взятого слева от точки рекомбинации первой последовательности и справа от точки рекомбинации второй последовательности [5, 6]. С филогенетической точки зрения перед рекомбинацией наследственный материал существующей последовательности был расположен на двух последовательностях – на одной он располагался слева от точки рекомбинации, на второй – справа от точки разрыва. В результате эволюционная история уже не может описываться одним деревом. Событие рекомбинации разбивает последовательности на две соседствующие области. История левой и правой областей может быть описана разными эволюционными деревьями. Рекомбинация создает различие между эволюционными деревьями, описывающими соседние области. Однако два соседних дерева не могут различаться произвольным образом; одно должно получаться из другого при помощи операции переноса поддеревьев. Когда происходит более одной рекомбинации, описать эволюционную историю можно при помощи списка эволюционных деревьев, каждое из которых соответствует некоторой области последовательностей, и каждое из которых может быть получено из предшественника путем нескольких операций переноса поддеревьев [6]. Вычисление расстояния переноса поддеревьев с линейной стоимостью полезно при реконструкции такого списка деревьев на базе подхода с максимальной экономичностью [5,6].
Открытые вопросы
1. Существует ли алгоритм аппроксимации с константным коэффициентом для вычисления расстояния обмена ближайшими соседями на невзвешенных эволюционных деревьях, или O(log n)-аппроксимация – лучшая из всех?
2. Является ли вычисление расстояния переноса поддеревьев с линейной стоимостью на взвешенных эволюционных деревьях NP-полной задачей, если неуникальные метки листьев не допускаются?
3. Можно ли улучшить коэффициент аппроксимации для вычисления расстояния переноса поддерева с линейной стоимостью на взвешенных эволюционных деревьях?
См. также
- Построение галловой филогенетической сети
- Поддерево максимального соответствия (для двух бинарных деревьев)
- Поддерево максимального соответствия (для трех или более деревьев)
- Построение филогенетического дерева из матрицы расстояний
Литература
1. DasGupta, B., He, X., Jiang, T., Li, M., Tromp, J.: On the linear-cost subtree-transfer distance. Algorithmica 25(2), 176-195 (1999)
2. DasGupta, B., He, X., Jiang, T., Li, M., Tromp, J., Zhang, L.: On distances between phylogenetic trees, 8th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 427-436 (1997)
3. DasGupta, B., He, X., Jiang, T., Li, M., Tromp, J., Wang, L., Zhang, L.: Computing Distances between Evolutionary Trees. In: Du, D.Z., Pardalos, P.M. (eds.) Handbook of Combinatorial Optimization. Kluwer Academic Publishers, Norwell, 2, 35-76 (1998)
4. DasGupta, B., He, X., Jiang, T., Li, M., Tromp, J., Zhang, L.: On Computing the Nearest Neighbor Interchange Distance. In: Du, D.Z., Pardalos, P.M., Wang, J. (eds.) Proceedings of the DIMACS Workshop on Discrete Problems with Medical Applications, DIMACS Series in Discrete Mathematics and Theoretical Computer Science. Am. Math. Soc. 55,125-143 (2000)
5. Hein, J.: Reconstructing evolution of sequences subject to recombination using parsimony. Math. Biosci. 98, 185-200 (1990)
6. Hein, J.: A heuristic method to reconstruct the history of sequences subject to recombination. J. Mol. Evol. 36, 396-405 (1993)
7. Hein, J., Jiang, T., Wang, L., Zhang, K.: On the complexity of comparing evolutionary trees. Discret. Appl. Math. 71, 153-169(1996)
8. Kuhner, M., Felsenstein, J.: A simulation comparison of phylogeny algorithms under equal and unequal evolutionary rates. Mol. Biol. Evol. 11(3),459-468 (1994)
9. Moore, G.W., Goodman, M., Barnabas, J.: An iterative approach from the standpoint of the additive hypothesis to the dendrogram problem posed by molecular data sets. J. Theor. Biol. 38, 423^57(1973)
10. Robinson, D.F.: Comparison of labeled trees with valency three. J Combinator. Theory Series B 11,105-119 (1971)