Коды Прюфера

Пусть T - дерево с множеством вершин $\{{\nu }_1,{\nu }_2,...,{\nu }_n\}$. Будем считать, что номер вершины ${\nu }_i$ равен $i$. Сопоставим дереву T последовательность $[a_1,a_2,...,a_{n-2}]$ называемую кодом Прюфера, по следующему правилу:

   функ КОД_ПРЮФЕРА(T: дерево) =
   1.    Пусть n - число вершин в T, а A - целочисленный вектор длины n-2;
   2.    B:= [1 : n];
   3.    для i от 1 до n-2 цикл
   4.        b:=min{k ∈ B; k - номер висячей вершины};
   5.        A[i]:= номер вершины, смежной вершине с номером b;
   6.        B:=B-{b};
   7.        Удалить из T вершину с номером b
         всё
   8     возврат A
   всё

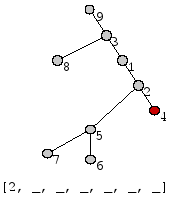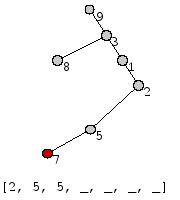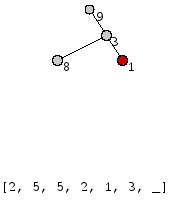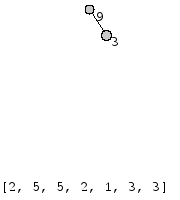
Рассмотрим седующий пример. Для дерева T (рис.) код Прюфера имеет вид:

$P_2(T)$ = [2, 5, 5, 2, 1, 3, 3].

Распаковка кода Прюфера осуществляется следующим образом:

   функ РАСПАКОВКА (A: код)=
   1.    Пусть T состоит из вершин $\{{\nu }_1,{\nu }_2,...,{\nu }_n\}$ таких, что номер вершины ${\nu }_i$ равен $i$,где n - длина кода A плюс 2;
   2.    B: = [1 : n];
   3.    для i от 1 до n+1 цикл
   4.        b:=min{k ∈ B ; k $\ne$ A[j] для любого j $\ge$ i};
   5.        В $T$ добавить ребро, соединяющее вершины с номерами $b$ и $A[i]$;
   6.        B:=B-{b}
         всё;
   7.    возврат T
   всё

В случае корневого ордерева процедуры построения кода Прюфера и его распаковки аналогичны. Необходимо только на последнем месте в $A$ указывать корневую вершину и при распаковке кода $A$ исключать номер этой вершины из множества $B$.

Операции над деревьями и кодами Прюфера

Будем считать, что вершины двух разных деревьев нумеруются различными числами, причём номера одного дерева всегда больше или меньше любого номера другого. Это требование часто выполняется в практических реализациях, т.к для вершин каждого дерева обычно отводят последовательные массивы номеров ячеек памяти. Если все номера дерева $T_1$ (или ориентированного дерева $\overrightarrow{T_1}$) меньше всех номерова дерева $T_2$ (или $\overrightarrow{T_2}$) то пишут $T_1$<$T_2$ (или $\overrightarrow{T_1}$<$\overrightarrow{T_2}$).

Рассмотрим следующие операции над деревьями:

$\stackrel{a}{\underset{b}{\downarrow }}$ - операция замены номера a вершины T на номер b;

$a\stackrel{0}{\to }b$ - операция склеивания двух деревьев по вершинам a и b, т.е. дерево $T_{1}a\stackrel{0}{\to }b{T}_2$ получается из $T_2$ и $T_1$ отождествлением вершин a из $T_1$ b из $T_2$ и присвоением склеенной вершине номера b (при склеивании ордеревьев добавляется требование, чтобы вершина b была корневой).

На рис 2.22 представлен результат выполнения операции $\overrightarrow{T_1}3\stackrel{0}{\to }10T_2$, где $\overrightarrow{T_1}$ и $\overrightarrow{T_2}$ - деревья, изображённые на рис. 2.20 и 2.21.

Рассмотрим некоторые вставки кода Прюфера: [] - операция формального отбрасывания квадратных скобок; определена на всех выражениях вида $[a_1,a_2,...,a_n],b,[b_1,b_2,...,b_m]$ и состоит в отбрасывании всех внутренних квадратных скобок и добавлении двух внешних;

$\stackrel{\ast }{c}$ -операция вставки кода Прюфера; если

$P_2(\overrightarrow{T_1})=[a_1,a_2,...,a_k,c,a_{k+2},...,a_{n-1}]$

и среди чисел $a_{k+2},a_{k+3},a_{n-1}$ нет числа c, то

$P_2(\overrightarrow{T_1})\stackrel{\ast }{c}{P}_2(\overrightarrow{T_2})=[a_1,a_2,...,a_k,P_2(\overrightarrow{T_2}),c,a_{k+2},...,a_{n-1}]$.

Справедливы следующие соотношения, связывающие операции над деревьями и кодами Прюфера:

если $T_1<T_2$, то

$P_2(T_{1}a\stackrel{0}{\to }b{T}_2)=[P_2(\stackrel{a}{\underset{b}{\downarrow }}{T}_1),b,P_2(T_2)];$

если $T_1>T_2$, то необходимо рассматривать дерево $T_{1}b\stackrel{0}{\to }a{T}_2$, и всё сводится к предыдущему случаю;

если $\overrightarrow{T_1}<\overrightarrow{T_2}$, то

$P_2(T_{1}a\stackrel{0}{\to }b{T}_2)=[P_2(\stackrel{a}{\underset{b}{\downarrow }}\overrightarrow{T_1}),\stackrel{\ast }{c},P_2(\overrightarrow{T_2})]$,

где $c$ - непосредственный предок вершины $a$ в дереве $\overrightarrow{T_1}$

если $\overrightarrow{T_1}>\overrightarrow{T_2}$, то

$P_2(T_{1}a\stackrel{0}{\to }b{T}_2)=[P_2(\overrightarrow{T_2}),P_2(\stackrel{a}{\underset{b}{\downarrow }}\overrightarrow{T_1})]$,