Самостабилизация: различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| Строка 47: | Строка 47: | ||
Одним из открытий, сделанных в ходе исследования самостабилизирующихся графовых алгоритмов, является разница между алгоритмами, которые завершают работу, и теми, которые постоянно меняют состояние даже после | Одним из открытий, сделанных в ходе исследования самостабилизирующихся графовых алгоритмов, является разница между алгоритмами, которые завершают работу, и теми, которые постоянно меняют состояние даже после стабилизации выходных результатов. Рассмотрим задачу построения остовного дерева с корнем в процессе r. Некоторые алгоритмы самостабилизируются на свойстве, заключающемся в том, что для каждого <math>p \ne r</math> переменная <math>u_p</math> ссылается на родителя p в остовном дереве, и состояние остается неизменным. Другим примером алгоритмов являются самостабилизирующиеся протоколы для циркуляции маркеров с тем побочным эффектом, что маршрут циркуляции маркеров формирует остовное дерево. Первый тип алгоритмов требует <math>O(lg \; n)</math> памяти на процесс, тогда как второй – <math>O(lg \; \delta)</math>, где <math>\delta</math> – степень (число соседей) процесса. Это различие было формализовано в понятии ''молчаливых'' алгоритмов, которые со временем перестают изменять какое бы то ни было значение в процессе коммуникации; в [5] для модели регистра связей было показано, что молчаливые алгоритмы для многих графовых задач требуют <math>\Omega(lg \; n)</math> памяти. | ||
Версия от 10:34, 1 августа 2022
Ключевые слова и синонимы
Аутопоэзис; гомеостаз; управление автономной системой
Постановка задачи
Алгоритм является самостабилизирующимся, если в конечном итоге он демонстрирует правильное поведение независимо от начального состояния. Общая цель заключается в разработке самостабилизирующихся решений для определенной задачи. В настоящее время известно, что свойство самостабилизации применимо для целого ряда задач в распределенных вычислениях. Самостабилизация важна для распределенных систем и сетевых протоколов, подверженных преходящим сбоям. Самостабилизирующиеся системы автоматически восстанавливаются после сбоев, которые повреждают их состояние.
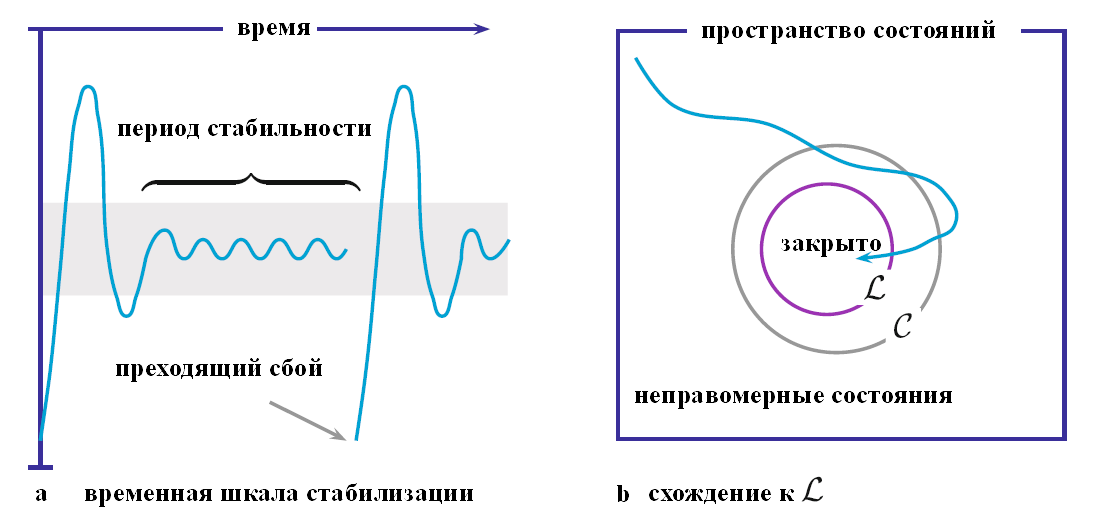
Операциональная интерпретация самостабилизации изображена на рис. 1. Часть (a) рисунка неформально изображает поведение самостабилизирующейся системы, где по оси x отложено время, а по оси y – некоторая неформальная мера корректности. Кривая иллюстрирует траекторию движения системы через последовательность состояний во время выполнения. На начальном этапе состояние системы некорректно; позже система входит в корректное состояние, затем возвращается в некорректное, после чего стабилизируется на неопределенный период, на протяжении которого все состояния корректны. Этот период стабильности нарушается преходящим сбоем, который переводит систему в некорректное состояние, после чего повторяется описанный выше сценарий. Часть (b) рисунка иллюстрирует сценарий в терминах предикатов состояния. В рамке представлен предикат true, который характеризует все возможные состояния. Предикат [math]\displaystyle{ \mathcal{C} }[/math] характеризует корректные состояния системы, а [math]\displaystyle{ \mathcal{L} \subset \mathcal{C} }[/math] представляет закрытый предикат правомерности. Достижение состояния в [math]\displaystyle{ \mathcal{L} }[/math] соответствует вступлению в период стабильности в части (a). Пусть имеется алгоритм A с таким типом поведения. Мы говорим, что A самостабилизируется в [math]\displaystyle{ \mathcal{L} }[/math]; когда имеется неявное понимание [math]\displaystyle{ \mathcal{L} }[/math], это утверждение упрощается до выражения «A самостабилизируется».
Рисунок 1. Траектории самостабилизации
Задача [3]. Первая формулировка задачи самостабилизации, предложенная Дейкстрой, представляет собой кольцо из n процессов с номерами от 0 до n - 1. Обозначим состояние процесса i как x[i]. Коммуникация в кольце однонаправленная с использованием модели совместно используемого состояния. Атомарный шаг процесса i может быть выражен защищенным назначением вида [math]\displaystyle{ g(x[i \ominus 1], x[i]) \to x[i]: = f(x[i \ominus 1], x[i]) }[/math]. Здесь [math]\displaystyle{ \ominus }[/math] – это вычитание по модулю n, так что [math]\displaystyle{ x[i \ominus 1] }[/math] представляет собой состояние предыдущего процесса в кольце по отношению к процессу i. Защищенное присваивание g – это булево выражение; если [math]\displaystyle{ g(x[i \ominus 1], x[i]) }[/math] истинно, то процесс i считается привилегированным (или включенным). Таким образом, за один атомарный шаг привилегированный процесс i считывает состояние предыдущего процесса и вычисляет новое состояние. Планирование выполнения контролируется центральным демоном, который справедливым образом выбирает один из всех разрешенных процессов для выполнения следующего шага. Задача заключается в выводе g и f таким образом, чтобы независимо от начальных состояний [math]\displaystyle{ x[i], 0 \le i \lt n }[/math], в конечном итоге оставалась одна привилегия, и каждый процесс пользовался привилегией бесконечно часто.
Метрики сложности
Сложность самостабилизации оценивается путем измерения ресурса, необходимого для сходимости из произвольного начального состояния. Наиболее широко в литературе по самостабилизации применяются метрики времени сходимости и объема памяти в наихудшем случае, требующиеся решающему данную задачу алгоритму. Кроме того, для реактивных самостабилизирующихся алгоритмов оцениваются метрики для стабильного поведения алгоритма, то есть начиная с его правомерного состояния, и сравниваются с нестабилизирующимися алгоритмами, чтобы измерить затраты на самостабилизацию.
Основные результаты
Композиция
Многие самостабилизирующиеся протоколы имеют многослойную конструкцию. Обозначим за [math]\displaystyle{ \{ A_i \}^{m - 1}_{i = 0} }[/math] множество программ, обладающих следующим свойством: для каждой переменной состояния x, если программа [math]\displaystyle{ A_i }[/math] записывает x, то ни одна программа [math]\displaystyle{ A_j }[/math] для j > i не записывает x. Программы в [math]\displaystyle{ \{ A_j \}^{m - 1}_{j = i + 1} }[/math] могут читать переменные, записанные [math]\displaystyle{ A_i }[/math], то есть использовать выходное значение [math]\displaystyle{ A_i }[/math] в качестве входа. Справедливая композиция программ B и C, записываемая в виде B [] C, предполагает справедливое планирование шагов B и C. Обозначим за [math]\displaystyle{ X_j }[/math] множество переменных, прочитанных [math]\displaystyle{ A_j }[/math] и, возможно, записанных [math]\displaystyle{ \{ A_i \}^{j - 1}_{i = 0} }[/math].
Теорема 1 (теорема о справедливой композиции [4]). Положим, что [math]\displaystyle{ A_i }[/math] самостабилизируется на [math]\displaystyle{ \mathcal{L}_i }[/math] в предположении, что все переменные в [math]\displaystyle{ X_i }[/math] остаются константными на протяжении любого выполнения; тогда [math]\displaystyle{ A_0 [] A_1 [] \cdot \cdot \cdot [] A_{m - 1} }[/math] самостабилизируется на [math]\displaystyle{ \{ \mathcal{L} \}^{m - 1}_{i = 0} }[/math].
Справедливая композиция с многослойным множеством [math]\displaystyle{ \{ A_i \}^{m - 1}_{i = 0} }[/math] соответствует последовательной композиции фаз распределенного алгоритма. Например, пусть B – самостабилизирующийся алгоритм взаимного исключения в сети, предполагающий существование корневого остовного дерева, а алгоритм C – самостабилизирующийся алгоритм построения корневого остовного дерева в связной сети; тогда B [] C – самостабилизирующийся алгоритм взаимного исключения для связной сети.
Задачи синхронизации
Один из вопросов, связанных с проблемой, поставленной в разделе «Постановка задачи», заключается в том, может ли существовать равномерное решение, в котором все процессы имеют идентичные алгоритмы. Результат Дейкстры для однонаправленного кольца представляет собой квазиравномерное решение (все процессы, кроме одного, имеют один и тот же алгоритм), использующее n состояний на процесс. Состояние каждого процесса – это счетчик: процесс 0 увеличивает счетчик по модулю k, где [math]\displaystyle{ k \ge n }[/math] достаточно для сходимости; остальные процессы копируют счетчик предыдущего процесса в кольце. В правомерном состоянии каждый раз, когда процесс 0 увеличивает счетчик, полученное значение отличается от значений всех остальных счетчиков в кольце. Этот кольцевой алгоритм оказывается самостабилизирующимся для распределенного демона (любое подмножество привилегированных процессов может выполняться параллельно), когда к > n. Последующие исследования установили, что взаимное исключение на однонаправленном кольце занимает [math]\displaystyle{ \Theta(1) }[/math] памяти на процесс для неравномерного решения. Детерминированные равномерные решения этой задачи в общем случае невозможны, кроме исключительного случая, когда n является простым. Известны рандомизированные равномерные решения для произвольного n, требующие [math]\displaystyle{ O(lg \; \alpha) }[/math] памяти, где [math]\displaystyle{ \alpha }[/math] – наименьшее число, не являющееся делителем n. Некоторые нижние границы памяти для равномерных решений получены в [7]. Временная сложность алгоритма Дейкстры составляет [math]\displaystyle{ O(n^2) }[/math] раундов, и было показано, что некоторые рандомизированные решения имеют ожидаемое время сходимости [math]\displaystyle{ O(n^2) }[/math].
Дейкстра также представил решение проблемы взаимного исключения для линейного массива процессов, используя O(1) памяти на процесс [3]. Позже этот результат был обобщен на корневое дерево процессов, но при этом взаимное исключение было ослаблено до наличия одной привилегии на любом пути от корня до листа. Последующие исследования развили эту тему, показав, что задачи распределенных вычислений распространения волны имеют самостабилизирующиеся решения. Также были решены задачи синхронизации фазы и синхронизации часов. Пример самостабилизирующегося взаимного исключения в многопроцессорной модели с совместно используемой памятью см. в работе [9].
Графовые алгоритмы
Сети коммуникаций обычно представляются моделями в виде графов, и потребность в распределенных графовых алгоритмах, устойчивых к преходящим сбоям, стимулирует изучение таких задач. В этой области получены такие результаты, как самостабилизирующиеся алгоритмы для остовных деревьев, поиска центра, поиска паросочетаний, проверки на планарность, раскраски, нахождения независимых множеств и другие. В общем случае все графовые задачи могут быть решены при помощи самостабилизирующихся алгоритмов: задачи, которые имеют на входе топологию сети и, возможно, связанные с ней коэффициенты, такие как веса ребер, и определяют выходные данные как функцию от входных, могут быть решены общими методами самостабилизации. Эти общие методы требуют значительных затрат времени и памяти, а также могут использовать более сильные предположения о модели, чем требуется для конкретных задач – например, уникальные идентификаторы процессов и предполагаемое ограничение на диаметр сети. Поэтому исследования алгоритмов на графах продолжаются.
Одним из открытий, сделанных в ходе исследования самостабилизирующихся графовых алгоритмов, является разница между алгоритмами, которые завершают работу, и теми, которые постоянно меняют состояние даже после стабилизации выходных результатов. Рассмотрим задачу построения остовного дерева с корнем в процессе r. Некоторые алгоритмы самостабилизируются на свойстве, заключающемся в том, что для каждого [math]\displaystyle{ p \ne r }[/math] переменная [math]\displaystyle{ u_p }[/math] ссылается на родителя p в остовном дереве, и состояние остается неизменным. Другим примером алгоритмов являются самостабилизирующиеся протоколы для циркуляции маркеров с тем побочным эффектом, что маршрут циркуляции маркеров формирует остовное дерево. Первый тип алгоритмов требует [math]\displaystyle{ O(lg \; n) }[/math] памяти на процесс, тогда как второй – [math]\displaystyle{ O(lg \; \delta) }[/math], где [math]\displaystyle{ \delta }[/math] – степень (число соседей) процесса. Это различие было формализовано в понятии молчаливых алгоритмов, которые со временем перестают изменять какое бы то ни было значение в процессе коммуникации; в [5] для модели регистра связей было показано, что молчаливые алгоритмы для многих графовых задач требуют [math]\displaystyle{ \Omega(lg \; n) }[/math] памяти.
Преобразование
Простое представление [3] обеспечивается абстрактной моделью вычислений, которая скрывает детали коммуникации, управления программой и атомарности. Самостабилизация становится более сложной при рассмотрении обычных архитектур, в которых имеются сообщения, буферы и счетчики команд. Возникает естественный вопрос: как преобразовать или усовершенствовать самостабилизирующиеся алгоритмы, выраженные в абстрактных моделях, превратив их в более практически ценные конкретные модели. В качестве примера рассмотрим проблему преобразования алгоритмов, написанных для центрального демона, в модель распределенного демона. Это преобразование можно свести к нахождению самостабилизирующегося алгоритма передачи маркера для модели распределенного демона, такого, что в конечном итоге никакие два соседних процесса не могут одновременно иметь маркер; несколько маркеров могут повысить эффективность преобразования.
Общие методы
Общая проблема построения самостабилизирующегося алгоритма для входной нереактивной задачи может быть решена с помощью стандартных инструментов распределенных вычислений: моментальный снимок, трансляция, сброс состояния системы и синхронизация – эти задачи являются конструктивными блоками, позволяющими непрерывно проверять глобальное состояние (в некоторых удачных случаях [math]\displaystyle{ \mathcal{L} }[/math] можно локально проверить и исправить). Эти конструктивные блоки имеют самостабилизирующиеся решения, что позволяет использовать общий подход.
Отказоустойчивость
Связь между самостабилизацией и преходящими сбоями явно подразумевается в определении. Самостабилизация также применима при выполнении задач, которые асинхронно изменяют входы, тихо выходят из строя и перезапускаются, а также производят возмущения в коммуникациях [10]. Одно из возражений против механизма самостабилизации, особенно при применении методов общего характера, заключается в том, что небольшой преходящий сбой может привести к необходимости исправления всей системы. Эта проблема была исследована, например, в [8], где было показано, как можно оптимизировать сходимость для ограниченного числа сбоев. Самостабилизация также сочетается с другими типами устойчивости к сбоям, хотя это не всегда возможно: задача подсчета количества процессов в кольце не имеет самостабилизирующегося решения в модели совместно используемого состояния, если возможно аварийное завершение процесса [1] – если только не предусмотрен детектор сбоев.
Применение
Многие сетевые протоколы самостабилизируются благодаря применению следующей простой стратегии: периодически они отбрасывают текущие данные и восстанавливают их из доверенных источников информации. Эта идея не работает в полностью асинхронных системах, но наличие часов реального времени позволяет использовать эту простую стратегию. Аналогичным образом сторожевые устройства с аппаратными таймерами могут обеспечить эффективную основу для самостабилизации [6].
См. также
Литература
1. Anagnostou, E., Hadzilacos, V.: Tolerating Transient and Permanent Failures. In: Distributed Algorithms 7th International Workshop. LNCS, vol. 725, pp. 174-188. Springer, Heidelberg (1993)
2. Cournier, A., Datta, A.K., Petit, F., Villain, V.: Snap-Stabilizing PIF Algorithm in Arbitrary Networks. In: Proceedings of the 22nd International Conference Distributed Computing Systems, pp. 199-206, Vienna, July 2002
3. Dijkstra, E.W.: Self Stabilizing Systems in Spite of Distributed Control. Commun. ACM 17(11), 643-644 (1974). See also EWD391 (1973) In: Selected Writings on Computing: A Personal Perspective, pp. 41-46. Springer, New York (1982)
4. Dolev, S.: Self-Stabilization. MIT Press, Cambrigde (2000)
5. Dolev, S., Gouda, M.G., Schneider, M.: Memory Requirements for Silent Stabilization. In: Proceedings of the 15th Annual ACM Symposium on Principles of Distributed Computing, pp. 27-34, Philadelphia, May 1996
6. Dolev, S., Yagel, R.: Toward Self-Stabilizing Operating Systems. In: 2nd International Workshop on Self-Adaptive and Autonomic Computing Systems, pp. 684-688, Zaragoza, August 2004
7. Israeli, A., Jalfon, M.: Token Management Schemes and Random Walks Yield Self-Stabilizing Mutual Exclusion. In: Proceedings of the 9th Annual ACM Symposium on Principles of Distributed Computing, pp. 119-131, Quebec City, August 1990
8. Kutten, S., Patt-Shamir, B.: Time-Adaptive Self Stabilization. In: Proceedings of the 16th Annual ACM Symposium on Principles of Distributed Computing, pp. 149-158, Santa Barbara, August 1997
9. Lamport, L.: The Mutual Exclusion Problem: Part II-Statement and Solutions. J. ACM 33(2), 327-348 (1986)
10. Varghese, G., Jayaram, M.: The Fault Span of Crash Failures. J. ACM 47(2), 244-293 (2000)