Построение суффиксного дерева в RAM: различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| Строка 39: | Строка 39: | ||
Отметим, что эта граница по памяти не является оптимальной, поскольку существуют <math> | \Sigma |^n\;</math> различных строк и, следовательно, суффиксных деревьев, тогда как n log n | Отметим, что эта граница по памяти не является оптимальной, поскольку существуют <math> | \Sigma |^n\;</math> различных строк и, следовательно, суффиксных деревьев, тогда как n log n бит позволяют представлять n! различных объектов. | ||
'''Теорема 2. Суффиксные деревья могут быть построены за оптимальное время, в частности: | '''Теорема 2. Суффиксные деревья могут быть построены за оптимальное время''', в частности: | ||
1. В случае алфавита константной длины суффиксное дерево T(S) для строки S длины n может быть построено за время O(n) [11, 12, 13]. В случае алфавита общего вида указанные алгоритмы требуют O(n log n) времени. | 1. В случае алфавита константной длины суффиксное дерево T(S) для строки S длины n может быть построено за время O(n) [11, 12, 13]. В случае алфавита общего вида указанные алгоритмы требуют O(n log n) времени. | ||
2. В случае целочисленного алфавита суффиксное дерево для строки S может быть построено за время O(n) [4, 9]. | 2. В случае целочисленного алфавита суффиксное дерево для строки S может быть построено за время O(n) [4, 9]. | ||
В общем случае существует естественная стратегия построения суффиксного дерева: все суффиксы итеративно вставляются в изначально пустую структуру. Такая стратегия непосредственно приводит к алгоритму с линейным временем | В общем случае существует естественная стратегия построения суффиксного дерева: все суффиксы итеративно вставляются в изначально пустую структуру. Такая стратегия непосредственно приводит к алгоритму с линейным временем построения в случае, если каждый суффикс может быть вставлен за константное время. Надо отметить, что нахождение точной позиции, в которую должен быть вставлен суффикс, представляет собой главную проблему алгоритма. | ||
| Строка 54: | Строка 55: | ||
Другой алгоритм в 1976 году предложил МакКрейт [11]. В этом алгоритме суффиксы вставляются в растущее дерево от самого длинного к самому короткому. Это упрощает процедуру обновления, а дополнительной структурой данных является только один вид ссылки: внутренняя вершина v с меткой пути P(v) = aw для некоторого символа <math>a \in \Sigma \;</math> и | Другой алгоритм в 1976 году предложил МакКрейт [11]. В этом алгоритме суффиксы вставляются в растущее дерево от самого длинного к самому короткому. Это упрощает процедуру обновления, а дополнительной структурой данных является только один вид ссылки: внутренняя вершина v с меткой пути P(v) = aw для некоторого символа <math>a \in \Sigma \;</math> и строки <math>w \in \Sigma^* \;</math> имеет суффиксную ссылку на вершину u с меткой пути P(u) = w. На рис. 1 суффиксные ссылки представлены пунктирными стрелками. Они часто соединяют вершины над точками вставки последовательно вставленных суффиксов, как в примере на рис. 1 для вершины с меткой пути «M» и корневой вершины при вставке суффиксов «MAMIA» и «AMIA». Это свойство позволяет перейти в следующую точку вставки без необходимости искать ее от корня дерева, в силу чего обеспечивается амортизированное константное время вставки одного суффикса. Отметим, что поскольку алгоритм МакКрейта обрабатывает суффиксы от самого длинного к самому короткому, а промежуточные структуры не являются суффиксными деревьями, алгоритм не является онлайновым. | ||
Еще один подход с линейным временем выполнения для алфавита константного размера представляет онлайн-алгоритм Укконена [12]; он читает текст слева направо и обновляет суффиксное дерево с амортизированным константным временем добавления одного символа. Этот алгоритм также использует суффиксные ссылки для быстрого поиска точек вставки для следующих суффиксов. Более того, поскольку за время одного обновления метки ребер всех концевых ребер должны быть дополнены новым символом, для расширения всех меток за константное время применяется хитрый фокус: все правые указатели концевых ребер ссылаются на | Еще один подход с линейным временем выполнения для алфавита константного размера представляет онлайн-алгоритм Укконена [12]; он читает текст слева направо и обновляет суффиксное дерево с амортизированным константным временем добавления одного символа. Этот алгоритм также использует суффиксные ссылки для быстрого поиска точек вставки для следующих суффиксов. Более того, поскольку за время одного обновления метки ребер всех концевых ребер должны быть дополнены новым символом, для расширения всех меток за константное время применяется хитрый фокус: все правые указатели концевых ребер ссылаются на одно и то же значение «[[конец строки]]», которое только что получило приращение. | ||
| Строка 92: | Строка 93: | ||
В некоторых приложениях используется так называемое обобщенное суффиксное дерево для нескольких строк; словарь получается путем построения суффиксного дерева для конкатенации соответствующих строк. Важный вопрос в контексте этого построения касается динамического обновления дерева по мере вставки и удаления строк из словаря. Точнее говоря, поскольку метки ребер хранятся в виде пар указателей на исходную строку, после удаления строки из словаря соответствующие указатели могут стать недействительными и будут требовать обновления. Алгоритм для решения этой задачи за амортизированное линейное время предложили Фиала и Грин [6], линейный алгоритм для наихудшего случая (и, следовательно, исполняемый в реальном времени) – Ферраджина и др. [5]. | В некоторых приложениях используется так называемое обобщенное суффиксное дерево для нескольких строк; словарь получается путем построения суффиксного дерева для конкатенации соответствующих строк. Важный вопрос в контексте этого построения касается динамического обновления дерева по мере вставки и удаления строк из словаря. Точнее говоря, поскольку метки ребер хранятся в виде пар указателей на исходную строку, после удаления строки из словаря соответствующие указатели могут стать недействительными и будут требовать обновления. Алгоритм для решения этой задачи за амортизированное линейное время предложили Фиала и Грин [6], линейный алгоритм для наихудшего случая (и, следовательно, исполняемый в реальном времени) – Ферраджина и др. [5]. | ||
== Применение == | == Применение == | ||
Версия от 10:17, 30 июня 2016
Ключевые слова и синонимы
Построение полнотекстового индекса
Постановка задачи
Суффиксное дерево – возможно, самая известная и изученная структура данных для индексирования строк, имеющая приложения во многих областях, связанных с анализом последовательностей. После его изобретения в начале семидесятых было разработано несколько подходов к эффективному построению суффиксного дерева строки для различных моделей вычислений. Наиболее перспективные подходы, строящие суффиксное дерево в оперативной памяти, представлены в данном обзоре.
Нотация
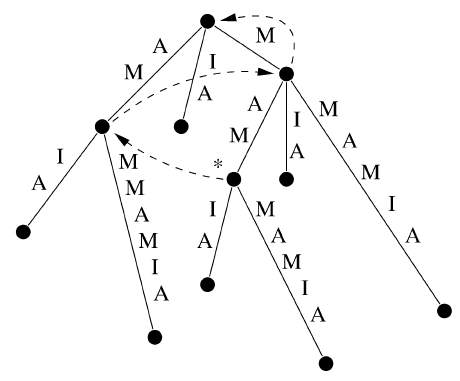
Пусть дан алфавит [math]\displaystyle{ \Sigma \; }[/math]. Trie-деревом над алфавитом [math]\displaystyle{ \Sigma \; }[/math] является корневое дерево, ребра которого помечены строками над S, такими, что никакие две метки ребер, выходящих из одной вершины, не начинаются с одного и того же символа. Trie-дерево является уплотненным, если все его внутренние вершины (возможно, за исключением корня) являются вершинами ветвления. Пусть дана конечная строка [math]\displaystyle{ S \in \Sigma^n \; }[/math]. Суффиксным деревом S, T(S), является уплотненное trie-дерево над [math]\displaystyle{ \Sigma \; }[/math], такое, что конкатенации меток ребер вдоль путей от корня до листьев являются суффиксами S. Пример суффиксного дерева приведен на рис. 1.
Рисунок 1. Суффиксное дерево для строки S = MAMMAMIA. Пунктирные стрелки обозначают суффиксные ссылки, используемые во всех эффективных алгоритмах построения суффиксного дерева
Конкатенация меток ребер от корня до вершины v дерева T(S) называется меткой пути v и обозначается P(v). Например, метка пути вершины, помеченной звездочкой на рис. 1, равна P(*) = MAM.
Ограничения
Временная сложность построения суффиксного дерева для строки S длины n зависит от размера базового алфавита [math]\displaystyle{ \Sigma \; }[/math]. Он может быть константным, может быть целочисленным [math]\displaystyle{ \Sigma = \{1, 2, ..., n \} \; }[/math], а может быть произвольным конечным множеством, элементы которого можно сравнивать за константное время. Заметим, что третий случай можно свести ко второму, если отобразить символы алфавита на множество {1, ..., n}, хотя при этом возникают дополнительные затраты на сортировку [math]\displaystyle{ \Sigma \; }[/math].
Задача 1 (построение суффиксного дерева)
Дано: конечная строка S длины n из символов алфавита [math]\displaystyle{ \Sigma \; }[/math].
Требуется: построить суффиксное дерево T(S).
Если предположить, что ребра, выходящие из каждой вершины, лексикографически упорядочены, что обычно имеет место, суффиксное дерево позволяет получить отсортированный порядок символов строки S за линейное время. Таким образом, построение суффиксного дерева наследует нижние границы сложности задачи сортировки: [math]\displaystyle{ \Omega(n \; log \; n) }[/math] в случае алфавита общего вида и [math]\displaystyle{ \Omega(n) \; }[/math] для целочисленных алфавитов.
Основные результаты
Теорема 1. Суффиксное дерево строки длины n требует [math]\displaystyle{ \Theta (n \; log \; n) }[/math] бит памяти.
Это легко показать, поскольку количество листьев T(S) не превышает n; то же относится к количеству внутренних вершин, которые согласно условию все являются ветвлениями, и к количеству ребер. Чтобы показать, что каждая метка ребра может быть размещена при помощи O(log n) бит памяти, вспомним, что метка ребра всегда является подстрокой строки S. Следовательно, она может быть представлена парой (I, r), состоящей из левого указателя I и правого указателя r для метки S[l, r].
Отметим, что эта граница по памяти не является оптимальной, поскольку существуют [math]\displaystyle{ | \Sigma |^n\; }[/math] различных строк и, следовательно, суффиксных деревьев, тогда как n log n бит позволяют представлять n! различных объектов.
Теорема 2. Суффиксные деревья могут быть построены за оптимальное время, в частности:
1. В случае алфавита константной длины суффиксное дерево T(S) для строки S длины n может быть построено за время O(n) [11, 12, 13]. В случае алфавита общего вида указанные алгоритмы требуют O(n log n) времени.
2. В случае целочисленного алфавита суффиксное дерево для строки S может быть построено за время O(n) [4, 9].
В общем случае существует естественная стратегия построения суффиксного дерева: все суффиксы итеративно вставляются в изначально пустую структуру. Такая стратегия непосредственно приводит к алгоритму с линейным временем построения в случае, если каждый суффикс может быть вставлен за константное время. Надо отметить, что нахождение точной позиции, в которую должен быть вставлен суффикс, представляет собой главную проблему алгоритма.
Первое решение этой задачи предложил Вейнер в своей основополагающей статье 1973 года [13]. Его алгоритм вставляет суффиксы от самого короткого к самому длинному, а точка вставки вычисляется за амортизированное константное время для алгоритма константного размера при помощи непрактичного количества дополнительных структур данных. Более простую версию алгоритма предложили Чен и Сейферас [3]. Они дали более четкое представление трех типов ссылок, необходимых для эффективного нахождения точек вставки суффиксов, а их доказательство сложности легко для понимания. Поскольку суффиксное дерево строится при чтении текста справа налево, эти два алгоритма иногда называют анти-онлайновыми.
Другой алгоритм в 1976 году предложил МакКрейт [11]. В этом алгоритме суффиксы вставляются в растущее дерево от самого длинного к самому короткому. Это упрощает процедуру обновления, а дополнительной структурой данных является только один вид ссылки: внутренняя вершина v с меткой пути P(v) = aw для некоторого символа [math]\displaystyle{ a \in \Sigma \; }[/math] и строки [math]\displaystyle{ w \in \Sigma^* \; }[/math] имеет суффиксную ссылку на вершину u с меткой пути P(u) = w. На рис. 1 суффиксные ссылки представлены пунктирными стрелками. Они часто соединяют вершины над точками вставки последовательно вставленных суффиксов, как в примере на рис. 1 для вершины с меткой пути «M» и корневой вершины при вставке суффиксов «MAMIA» и «AMIA». Это свойство позволяет перейти в следующую точку вставки без необходимости искать ее от корня дерева, в силу чего обеспечивается амортизированное константное время вставки одного суффикса. Отметим, что поскольку алгоритм МакКрейта обрабатывает суффиксы от самого длинного к самому короткому, а промежуточные структуры не являются суффиксными деревьями, алгоритм не является онлайновым.
Еще один подход с линейным временем выполнения для алфавита константного размера представляет онлайн-алгоритм Укконена [12]; он читает текст слева направо и обновляет суффиксное дерево с амортизированным константным временем добавления одного символа. Этот алгоритм также использует суффиксные ссылки для быстрого поиска точек вставки для следующих суффиксов. Более того, поскольку за время одного обновления метки ребер всех концевых ребер должны быть дополнены новым символом, для расширения всех меток за константное время применяется хитрый фокус: все правые указатели концевых ребер ссылаются на одно и то же значение «конец строки», которое только что получило приращение.
Рассматривается еще более строгий подход к онлайн-алгоритму, а именно алгоритм реального времени, имеющий сложность в наихудшем случае вместо амортизированной. Амир и др. [1] представили алгоритм построения суффиксного дерева для алфавита общего вида, требующий O(log n) времени на обновление одного символа в наихудшем случае при чтении текста справа налево; общее время его выполнения составляет O(n log n), как и у других упоминавшихся алгоритмов для алфавита общего вида. Этот показатель достигается благодаря использованию бинарного дерева поиска на суффиксах текста, дополненного добавочными указателями, представляющими лексикографический и текстовый порядок суффиксов; такое дерево получило название сбалансированной структуры индексирования. Оно может быть построено за время O(log n) для одного добавленного символа в наихудшем случае и позволяет поддерживать суффиксное дерево в тех же временных рамках.
Первый алгоритм с линейным временем выполнения для построения суффиксного дерева на целочисленном алфавите предложили Фарах и Колтон [4]. Он использует так называемую четно-нечетную технику в три этапа:
1. Рекурсивно вычислить уплотненное trie-дерево всех суффиксов S, начинающихся с нечетных позиций; обозначим его [math]\displaystyle{ T_o \; }[/math].
2. Вывести из [math]\displaystyle{ T_o \; }[/math] уплотненное trie-дерево всех суффиксов S, начинающихся с четных позиций, обозначаемое [math]\displaystyle{ T_e \; }[/math].
3. Слить [math]\displaystyle{ T_o \; }[/math] и [math]\displaystyle{ T_e \; }[/math] в целое суффиксное дерево T(S).
Основная идея первого этапа заключается в кодировании пар символов как единичных символов. Поскольку могут встретиться только n/2 таких различных символов, они могут быть поразрядно отсортированы с сокращением диапазона до алфавита размера n/2. Таким образом, строка S длины n над целочисленным алфавитом [math]\displaystyle{ \Sigma = \{ 1, ..., n \} \; }[/math] переводится за время O(n) в строку S' длины n/2 над целочисленным алфавитом [math]\displaystyle{ \Sigma' = \{ 1, ..., n/2 \} \; }[/math]. Рекурсивное применение этого алгоритма дает в итоге суффиксное дерево S'. После перевода меток ребер из подстрок S' обратно в подстроки S могут встречаться вершины с исходящими ребрами, метки которых начинаются с одного и того же символа, поскольку два различных символа из [math]\displaystyle{ \Sigma' \; }[/math] могут быть парами с одним и тем же первым символом из [math]\displaystyle{ \Sigma \; }[/math]. В таких случаях свойство trie-дерева может быть восстановлено при помощи локальных модификаций меток ребер или добавления дополнительных вершин, в результате чего будет получено требуемое дерево [math]\displaystyle{ T_o \; }[/math].
На втором этапе полученное «нечетное» дерево [math]\displaystyle{ T_o \; }[/math] используется для генерации лексикографически отсортированного списка суффиксов, начинающихся с нечетных позиций. Поразрядная сортировка этих суффиксов со значениями символов в предшествующих четных позициях в качестве ключей позволяет получить лексикографически отсортированный список четных суффиксов за линейное время. Наряду с самыми длинными общими префиксами последовательных позиций, которые могут быть вычислены из [math]\displaystyle{ T_o \; }[/math] за линейное время при помощи запросов по поводу самого низкого общего предка и равенства
[math]\displaystyle{ lcp(l_{2i}, l_{2j}) = lcp(l_{2i + 1}, l_{2j + 1}) \; }[/math], если S[2i] = S[2j], и 0 в противном случае
это упорядочение позволяет реконструировать «четное» дерево [math]\displaystyle{ T_e \; }[/math] за линейное время.
На третьем этапе два trie-дерева [math]\displaystyle{ T_o \; }[/math] и [math]\displaystyle{ T_e \; }[/math] сливаются в суффиксное дерево T(S). Концептуально эта процедура достаточно проста: выполняется параллельный обход двух trie-деревьев, и каждая часть, присутствующая в одном или обоих деревьях, включается в общую структуру. Однако эта процедура проста только в случае, если ребра обходятся символ за символом, таким образом, чтобы подобные общие и различающиеся фрагменты можно было наблюдать непосредственно. Такой обход потребует [math]\displaystyle{ O(n^2) \; }[/math] времени в наихудшем случае, что существенно ухудшит общее линейное время выполнения. Поэтому Фарах и Колтон предлагают использовать оракула, который для ребра из [math]\displaystyle{ T_o \; }[/math] и ребра из [math]\displaystyle{ T_e \; }[/math] сообщает длину их общего префикса. Однако предложенный оракул может переоценивать длину, в результате чего сгенерированное дерево иногда требует коррекции, называемой отделением. Полное описание оракула и процедуры отделения см. в [4].
В целом, если на построение суффиксного дерева для строки [math]\displaystyle{ S \in \{ 1, ..., n \}^n \; }[/math] идет T(n) времени, то первый шаг занимает T(n/2) + O(n) времени, а второй и третий – O(n); таким образом, вся процедура занимает O(n) времени на RAM-модели.
Еще один онлайн-алгоритм построения суффиксных деревьев для целочисленных алфавитов заключается в построении за линейное время суффиксных массивов одновременно с ведением таблицы самых длинных общих префиксов, которое предложили Карккайнен и Сандерс в [9].
В некоторых приложениях используется так называемое обобщенное суффиксное дерево для нескольких строк; словарь получается путем построения суффиксного дерева для конкатенации соответствующих строк. Важный вопрос в контексте этого построения касается динамического обновления дерева по мере вставки и удаления строк из словаря. Точнее говоря, поскольку метки ребер хранятся в виде пар указателей на исходную строку, после удаления строки из словаря соответствующие указатели могут стать недействительными и будут требовать обновления. Алгоритм для решения этой задачи за амортизированное линейное время предложили Фиала и Грин [6], линейный алгоритм для наихудшего случая (и, следовательно, исполняемый в реальном времени) – Ферраджина и др. [5].
Применение
Суффиксное дерево поддерживает множество приложений, в большинстве своем являющихся оптимальными по времени и объему памяти, в числе которых можно упомянуть точное сравнение строк, сравнение множеств, нахождение самой длинной общей подстроки в двух или нескольких последовательностях, сравнение суффиксов и префиксов для всех пар, поиск повторов и сжатие текста. Эти и некоторые другие приложения, большинство которых относятся к области биоинформатики, представлены в работах [2] и [8].
Открытые вопросы
Некоторые теоретические вопросы, касающиеся ожидаемого размера и структуры ветвления суффиксных деревьев в рамках более сложных моделей последовательностей, чем независимые одинаково распределенные случайные величины, остаются открытыми. В настоящее время большинство исследований посвящены более экономичным по объему памяти структурам данных – таким как суффиксные массивы и индексы сжатых строк.
Экспериментальные результаты
Суффиксные деревья печально известны своими высокими требованиями к памяти. Фактическое потребление памяти на практике оказывается в 9-11 раз больше размера индексируемой строки даже для самых экономичных из известных на данный момент вариантов [7,10]. Кроме того, в работе [7] также показано, что субоптимальные алгоритмы – такие как очень простой алгоритм, выполняющий только запись сверху вниз (WOTD) за квадратичное время – могут превосходить по эффективности оптимальные алгоритмы во многих случаях реальных вычислений при условии грамотной организации.
Ссылка на код
Несколько библиотек анализа последовательностей содержат код для построения суффиксного дерева. Например, библиотека Strmat (http://www. cs.ucdavis.edu/~gusfield/strmat.html, Гусфилд и др.) содержит реализации алгоритмов Вейнера и Укконена. Реализацию WOTD-алгоритма Курца можно найти по адресу http://bibiserv.techfak. uni-bielefeld.de/wotd.
См. также
- Индексация сжатого текста
- Сортировка строк
- Построение суффиксного массива
- Построение суффиксного дерева в иерархической памяти
- Индексация текста
Литература
1. Amir, A., Kopelowitz, T., Lewenstein, M., Lewenstein, N.: Towards real-time suffix tree construction. In: Proceedings of the 12th International Symposium on String Processing and Information Retrieval, SPIRE 2005. LNCS, vol. 3772, pp. 67-78. Springer, Berlin (2005)
2. Apostolico, A.: The myriad virtues of subword trees. In: Apostolico, A., Galil, Z. (eds.) Combinatorial Algorithms on Words. NATO ASI Series, vol. F12, pp. 85-96. Springer, Berlin (1985)
3. Chen, M.T., Seiferas, J.: Efficient and elegant subword tree construction. In: Apostolico, A., Galil, Z. (eds.) Combinatorial Algorithms on Words. Springer, New York (1985)
4. Farach, M.: Optimal suffix tree construction with large alphabets. In: Proc. 38th Annu. Symp. Found. Comput. Sci., FOCS 1997, pp. 137-143. IEEE Press, New York (1997)
5. Ferragina, P., Grossi, R., Montangero, M.: A note on updating suffix tree labels. Theor. Comput. Sci. 201, 249-262 (1998)
6. Fiala, E.R., Greene, D.H.: Data compression with finite windows. Commun. ACM 32,490-505 (1989)
7. Giegerich, R., Kurtz, S., Stoye, J.: Efficient implementation of lazy suffix trees. Softw. Pract. Exp. 33,1035-1049 (2003)
8. Gusfield, D.: Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology. Cambridge University Press, New York (1997)
9. Karkkainen, J., Sanders, P.: Simple linear work suffix array construction. In: Proceedings of the 30th International Colloquium on Automata, Languages, and Programming, ICALP 2003. LNCS, vol. 2719, pp. 943-955. Springer, Berlin (2003)
10. Kurtz, S.: Reducing the space requirements of suffix trees. Softw. Pract. Exp. 29,1149-1171 (1999)
11. McCreight, E.M.: A space-economical suffix tree construction algorithm. J. ACM 23, 262-272 (1976)
12. Ukkonen, E.: On-line construction of suffix trees. Algorithmica 14,249-260(1995)
13. Weiner, P.: Linear pattern matching algorithms. In: Proc. of the 14th Annual IEEE Symposium on Switching and Automata Theory, pp. 1-11. IEEE Press, New York (1973)