Планарные геометрические остовы

Ключевые слова и синонимы

Геометрическая сеть; протяженность; обход

Постановка задачи

Пусть S – множество точек на плоскости, а G – неориентированный граф с множеством вершин S, каждое ребро (u, v) которого имеет вес, равный евклидовому расстоянию |uv| между точками u и v. Для любых двух точек p и q в S обозначим кратчайший путь между ними в графе G за ${\delta }_G(p,q)$. Если $t\ge 1$ – вещественное число, то граф G является t-остовом S в случае, если ${\delta }_G(p,q)\le t|pq|$ для любых двух точек p и q в S. Таким образом, если значение t близко к 1, то граф G содержит достаточно хорошие приближения $(\genfrac{}{}{0ex}{}{n}{2})$ евклидовых расстояний, определяемых парами точек в S. Если к тому же G содержит O(n) ребер, то этот граф можно считать разреженным приближением полного графа на S. Наименьшее значение f, при котором G будет являться t-остовом, называется коэффициентом растяжения (или протяженностью) G. Исчерпывающий обзор геометрических остовов можно найти в работе Нарасимхана и Смида [16].

Предположим, что каждое ребро (u, v) графа G реализовано в видео отрезка прямой, соединяющей точки u и v. Граф G называется планарным, если его ребра пересекаются только в точках их общих вершин.

Далее будут рассмотрены две задачи:

Задача 1. Определить наименьшее вещественное число t > 1, для которого выполняется следующее утверждение: Для каждого множества S из n точек на плоскости существует плоский граф с множеством вершин S, являющийся t-остовом для S. Разработать эффективный алгоритм построения такого плоского t-остова.

Задача 2. Определить наименьшее целое положительное число D, для которого выполняется следующее утверждение: Существует константное значение t, такое, что для каждого множества S из n точек на плоскости существует плоский граф с множеством вершин S и максимальной степенью, не превышающей D, который является t-остовом для S. Разработать эффективный алгоритм построения такого плоского t-остова.

Основные результаты

Пусть S – конечном множество точек на плоскости, имеющих общее положение; т.е. никакие три точки из S не лежат на одной прямой и никакие четыре – на одной окружности. Триангуляцией Делоне для множества S является плоский граф с множеством вершин S, в котором (u, v) является ребром в том и только том случае, если существует окружность, проходящая через u и v, внутри которой не содержится ни одной точки S. (Поскольку точки S находятся в общем положении, этот гарф представляет собой триангуляцию). Триангуляция Делоне на множестве из n точек на плоскости может быть построена за время O(n log n). Добкин, Фридман и Суповит [10] первыми показали, что коэффициент растяжения триангуляции Делоне ограничен константой. Они доказали, что триангуляция Делоне является t-остовом для $t=\pi (1+\sqrt{5})/2$. Наилучшую известную на данный момент верхнюю границу коэффициента растяжения для этого графа предложили Кил и Гутвин [12]:

Теорема 1. Пусть S – конечное множество точек на плоскости. Триангуляция Делоне для множества S является t-остовом S при $t=4\pi \sqrt{3}/9$.

Несколько более строгий результат был доказан Бозе и др. [3]. Они доказали, что для любых двух точек p и q из S триангуляция Делоне содержит путь между p и q, длина которого не превышает $t=4\pi \sqrt{3}/9|pq|$, а длина каждого ребра на этом пути не превышает |pq|.

Левкопулос и Лингас [14] обобщили результат теоремы 1: Предположим, что дана триангуляция Делоне для множества S. Тогда для любого вещественного числа r > 0 за время O(n) можно построить плоский граф G с множеством вершин S, являющийся t-остовом для S, где $t=(1+1/r)4\pi \sqrt{3}/9$, совокупная длина ребер которого будет не более чем в 2r + 1 раз превышать вес остовного дерева для S.

Триангуляцию Делоне можно иначе определить как двойственную конструкцию по отношению к диаграмме Вороного на множестве S. Рассматривая диаграмму Вороного для метрики, отличной от евклидовой, получаем соответствующую триангуляцию Делоне. Чу [7] показал, что триангуляция Делоне на основе манхэттенского расстояния представляет собой $\sqrt{10}$-остов (в этом остове длины путей измеряются при помощи евклидовой метрики). Чу [8] также дал наилучшее известное на сегодня решение задачи 1:

Теорема 2. Пусть S – конечное множество точек на плоскости. Рассмотрим триангуляцию Делоне для S, основанную на выпуклой функции расстояния, определяемой при помощи равностороннего треугольника. Этот плоский граф является 2-остовом для S (в котором длины путей измеряются при помощи евклидовой метрики).

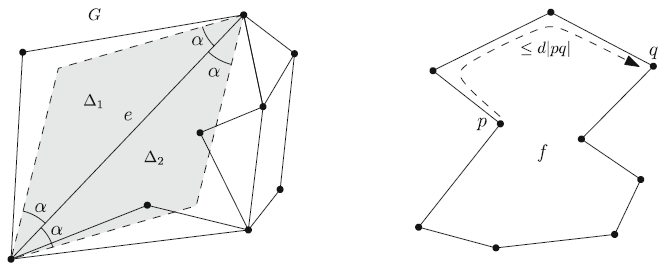
Дас и Джозеф [9] следующим образом обобщили утверждение теоремы 1 (см. рисунок). Пусть G – плоский граф с множеством вершин S, а $\alpha$ – вещественное число, $0<\alpha <\pi /2$. Для любого ребра e графа G обозначим за ${\mathrm{\Delta }}_1$ и ${\mathrm{\Delta }}_2$ два равнобедренных треугольника с основанием e и углом при основании $\alpha$. Ребро e удовлетворяет свойству $\alpha$-ромба, если по меньшей мере один из треугольников ${\mathrm{\Delta }}_1$ и ${\mathrm{\Delta }}_2$ не содержит внутри точек множества S. Плоский граф G удовлетворяет свойству $\alpha$-ромба, если каждое ребро e графа G удовлетворяет этому свойству. Для вещественного числа $d\ge 1$ граф G удовлетворяет свойству d-хорошего многоугольника, если для каждой грани f графа G и для каждых двух вершин p и q на границе f, таких, что соединяющий их отрезок прямой полностью находится в f, длина пути между p и q вдоль границы f не превышает d|pq|. Дас и Джозеф [9] доказали, что любой плоский граф, удовлетворяющий одновременно свойству $\alpha$-ромба и свойству d-хорошего многоугольника, является t-остовом для некоторого вещественного числа t, которое зависит только от $\alpha$ и d. Значение t было несколько улучшено Ли [13]:

С левой стороны изображено свойство $\alpha$-ромба. По меньшей мере один из треугольников ${\mathrm{\Delta }}_1$ и ${\mathrm{\Delta }}_2$ не содержит внутри точек множества S. Справа проиллюстрировано свойство d-хорошего многоугольника. p и q – две вершины на одной и той же грани f, которые видят друг друга. По меньшей мере один из двух путей между p и q вдоль границы f имеет длину, не превышающую d|pq|

Теорема 3. Пусть $\alpha \in (0,\pi /a)$ и $d\ge 1$ – вещественные числа, а G – плоский граф, удовлетворяющий свойствам $\alpha$-ромба и d-хорошего многоугольника. В таком случае граф G является t-остовом для множества вершин G, где $t=\frac{8(\pi -\alpha {)}^{2}d}{{\alpha }^{2}si{n}^2(\alpha /4)}$.

В качестве примера нетрудно показать, что триангуляция Делоне удовлетворяет свойству $\alpha$-ромба при $\alpha =\pi /4$. Дрисдейл и др. [11] показали, что триангуляция с минимальным весом удовлетворяет свойству $\alpha$-ромба при $\alpha =\pi /4,6$. Наконец, у Ли [13] было показано, что жадная триангуляция удовлетворяет свойству $\alpha$-ромба при $\alpha =\pi /6$. Разумеется, любая триангуляция удовлетворяет свойству d-хорошего многоугольника при d = 1.

Теперь рассмотрим задачу 2, касающуюся построения плоских остовов с невысокой максимальной степенью. Первый результат для этой задачи был получен Бозе и др. [2]. Они доказали, что триангуляция Делоне любого конечного множества точек содержит подграф с максимальной степенью не выше 27, являющийся t-остовом (для некоторого константного t). Ли и Ван [15] улучшили этот результат, показав, что триангуляция Делоне содержит t-остов со степенями не более 23. Если имеется триангуляция Делоне, подграфы в [2, 15] можно построить за время O(n). Лучший известный на сегодня результат для задачи 2 дали Бозе и др. [6]:

Теорема 4. Пусть S – множество n точек на плоскости. Триангуляция Делоне для множества S содержит подграф с максимальной степенью не выше 17, являющийся t-остовом S для некоторого константного t. Если имеется триангуляция Делоне, этот подграф можно построить за время O(n).

На самом деле результат оказался даже более общим:

Теорема 5. Пусть S – множество из n точек на плоскости, $\alpha \in (0,\pi /2)$ – вещественное число, а G – триангуляция S, удовлетворяющая свойству $\alpha$-ромба. Тогда G содержит подграф с максимальной степенью не выше $14+\lceil 2\pi /\alpha \rceil$, являющийся t-остовом S, где t зависит только от a. Если имеется триангуляция G, этот подграф можно построить за время O(n).

Применение

Плоские остовы применяются при решении задач поиска путей и маршрутизации в режиме онлайн, которые возникают, например, в географических информационных системах и сетях коммуникаций. В этих областях применения, как правило, среда в целом неизвестна, и маршрутизацию приходится осуществлять, зная только местонахождение источника, точку назначения и ближайших соседей текущей позиции. Бозе и Морин [4, 5] показали, что в рамках этой модели имеются эффективные стратегии маршрутизации для планарных графов, такие как триангуляция Делоне и графы, одновременно удовлетворяющие свойствам $\alpha$-ромба и d-хорошего многоугольника. Эти стратегии являются конкурентными в том смысле, что длины рассчитанных путей не превышают произведения евклидова расстояния между источником и получателем на константный коэффициент. Кроме того, эти стратегии маршрутизации требуют ограниченного количества памяти.

Открытые вопросы

Ни одно из решений задач 1 и 2, приведенных в разделе «Основные результаты», не является оптимальным. Следующие задачи остаются открытыми:

1. Определить наименьшее вещественное число t, при котором триангуляция Делоне любого конечного множества точек на плоскости является t-остовом. Распространено мнение, что $t=\pi /2$. Согласно теореме 1, $t\le 4\pi \sqrt{3}/9$.

2. Определить наименьшее вещественное число t, при котором для любого конечного множества точек на плоскости существует плоский t-остов. Согласно теореме 2, $t\le 2$. Если взять частный случай S в виде множества из четырех вершин квадрата, получается, что t должно быть не меньше $\sqrt{2}$.

3. Определить наименьшее целое число D, при котором триангуляция Делоне любого конечного множества точек на плоскости содержит t-остов (для некоторого константного значения t), максимальная степень которого не превышает D. Согласно теореме 4, $D\le 17$. Из результатов, полученных Ароновым и др. [1], следует, что значение D должно быть не меньше 3.

4. Определить наименьшее вещественное число D, при котором для любого конечного множества точек на плоскости существует плоский t-остов (для некоторого константного значения t), максимальная степень которого не превышает D. Согласно теореме 4 и результатам из работы [1], $3\le D\le 17$.

См. также

• Применение геометрических остовных сетей
• Протяженность геометрических сетей
• Геометрические остовы
• Разреженные остовы графов

Литература

1. Aronov, B., de Berg, M., Cheong, O., Gudmundsson, J., Haverkort, H., Vigneron, A.: Sparse geometric graphs with small dilation. In: Proceedings of the 16th International Symposium on Algorithms and Computation. Lecture Notes in Computer Science, vol. 3827, pp. 50-59. Springer, Berlin (2005)

2. Bose, P., Gudmundsson, J., Smid, M.: Constructing plane spanners of bounded degree and low weight. Algorithmica 42, 249-264 (2005)

3. Bose, P., Maheshwari, A., Narasimhan, G., Smid, M., Zeh, N.: Approximating geometric bottleneck shortest paths. Comput. Geom.: Theory Appl. 29, 233-249 (2004)

4. Bose, P., Morin, P.: Competitive online routing in geometric graphs. Theor. Comput. Sci. 324,273-288 (2004)

5. Bose, P., Morin, P.: Online routing in triangulations. SIAM J. Comput. 33,937-951 (2004)

6. Bose, P., Smid, M., Xu, D.: Diamond triangulations contain spanners of bounded degree. In: Proceedings of the 17th International Symposium on Algorithms and Computation. Lecture Notes in Computer Science, vol. 4288, pp. 173-182. Springer, Berlin (2006)

7. Chew, L.P.: There is a planar graph almost as good as the complete graph. In: Proceedings of the 2nd ACM Symposium on Computational Geometry, pp. 169-177 (1986)

8. Chew, L.P.: There are planar graphs almost as good as the com plete graph. J. Comput. Syst. Sci. 39,205-219 (1989)

9. Das, G., Joseph, D.: Which triangulations approximate the complete graph? In: Proceedings of the International Symposium on Optimal Algorithms. Lecture Notes in Computer Science, vol.401, pp. 168-192. Springer, Berlin (1989)

10. Dobkin,D.P., Friedman, S.J., Supowit, K.J.:Delaunay graphs are almost as good as complete graphs. Discret. Comput. Geom. 5, 399^07(1990)

11. Drysdale, R.L., McElfresh, S., Snoeyink, J.S.: On exclusion regions for optimal triangulations. Discrete Appl. Math. 109, 49-65(2001)

12. Keil, J.M., Gutwin, C.A.: Classes of graphs which approximate the complete Euclidean graph. Discrete Comput. Geom. 7, 13-28(1992)

13. Lee, A.W.: Diamonds are a plane graph's best friend. Master's thesis, School of Computer Science, Carleton University, Ottawa (2004)

14. Levcopoulos, C., Lingas, A.: There are planar graphs almost as good as the complete graphs and almost as cheap as minimum spanning trees. Algorithmica 8,251-256 (1992)

15. Li, X.-Y., Wang, Y.: Efficient construction of low weighted bounded degree planar spanner. Int. J. Comput. Geom. Appl. 14,69-84(2004)

16. Narasimhan, G., Smid, M.: Geometric Spanner Networks. Cambridge University Press, Cambridge, UK (2007)