Минимальное время завершения для взвешенной системы

Ключевые слова и синонимы

Среднее время завершения для взвешенной системы

Постановка задачи

Задача нахождения минимального времени завершения для взвешенной системы представляет собой (1) набор J из n заданий, каждому из которых присвоены положительный вес ([math]\displaystyle{ w_j \; }[/math] для [math]\displaystyle{ j \in J \; }[/math]) и дата запуска [math]\displaystyle{ r_j \; }[/math], ранее которой это задание не может быть спланировано; (2) набор из m вычислительных машин, каждая из которых может обрабатывать не более одного задания в одно и то же время; (3) произвольный набор положительных значений [math]\displaystyle{ \{ p_{i, j} \} \; }[/math], где [math]\displaystyle{ p_{i, j} \; }[/math] обозначает время обработки задания j на машине i. План представляет собой назначение заданий машинам и выбор порядка их обработки. Обозначим за [math]\displaystyle{ C_j \; }[/math] время завершения задания j в рамках выполнения конкретного плана. Определим время завершения для взвешенной системы как [math]\displaystyle{ \sum_{j \in J} w_j C_j \; }[/math]. Задача заключается в вычислении плана, имеющего минимальное время завершения.

В нотации планирования, введенной Грэмом и др. [7], задача планирования задается триплетом [math]\displaystyle{ \alpha | \beta | \gamma \; }[/math], где [math]\displaystyle{ \alpha \; }[/math] обозначает машинную среду, [math]\displaystyle{ \beta \; }[/math] – дополнительные ограничения для заданий, а [math]\displaystyle{ \gamma \; }[/math] – целевую функцию. В данном случае нас главным образом будут интересовать значения параметра [math]\displaystyle{ \alpha \; }[/math], равные 1, P, R или Rm, которые означают, соответственно, одну машину, идентичные параллельные машины (то есть для фиксированного задания j и для каждой машины i [math]\displaystyle{ p_{i,j} \; }[/math] равно значению [math]\displaystyle{ p_j \; }[/math], независимому от i), несвязанные машины (значения [math]\displaystyle{ p_{i,j} \; }[/math] зависят и от задания i, и от машины j) и фиксированное количество m (не являющееся компонентом входных данных) несвязанных машин. Поле [math]\displaystyle{ \beta \; }[/math] принимает следующие значения: [math]\displaystyle{ r_j \; }[/math] обозначает, что у заданий имеются даты запуска; pmtn – что разрешено вытеснение заданий; prec – что задача может включать отношения предшествования между заданиями, что также налагает ограничения на составление плана. Поле [math]\displaystyle{ \gamma \; }[/math] содержит значения [math]\displaystyle{ \sum w_j C_j \; }[/math] либо [math]\displaystyle{ \sum C_j \; }[/math], которые соответствуют полному времени завершения для взвешенной системы и для невзвешенной системы, соответственно.

Некоторые из более простых классов задач поиска минимального времени завершения для взвешенной системы допускают использование оптимальных решений с полиномиальным временем выполнения. Среди них можно упомянуть задачу [math]\displaystyle{ P || \sum C_j \; }[/math], для которой оптимальной является стратегия «самое короткое задание планировать первым»; [math]\displaystyle{ 1 || \sum w_j C_j \; }[/math], для которой оптимальным является следование правилу Смита [13] (планирование заданий в порядке неубывания значений [math]\displaystyle{ p_j / w_j \; }[/math]); [math]\displaystyle{ R || \sum C_j \; }[/math], которая может быть решена при помощи техник сопоставления [2, 9]. При введении дат запуска даже простейшие классы задач минимизации времени завершения для взвешенной системы становятся строго недетерминированными с полиномиальным временем выполнения (NP-полными). Подход Афрати и др. [1] заключается в разработке схем аппроксимации с полиномиальным временем выполнения (PTAS) для нескольких классов задач планирования, способствующих минимизации времени завершения для взвешенной системы с указанием дат запуска. До публикации упомянутой работы лучшие решения для минимизации времени завершения для взвешенной системы с указанием дат запуска представляли собой алгоритмы O(1)-аппроксимации (см., например, [4, 5, 11]); единственный известный PTAS-алгоритм для сильной NP-полной задачи, рассматривающей время завершения для взвешенной системы, предложили Скутелла и Вёгингер [12], разработавшие PTAS для задачи [math]\displaystyle{ P || \sum w_j C_j \; }[/math]. Исчерпывающий обзор задач поиска минимального времени завершения для взвешенной системы составили Чекури и Ханна [3].

Основные результаты

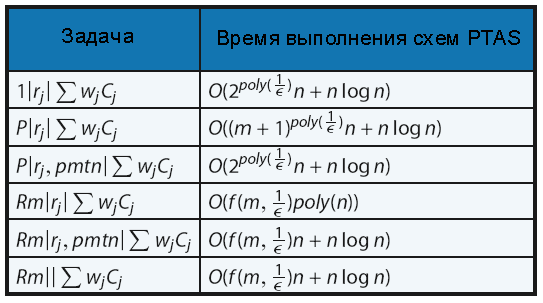
Афрати и др. [1] первыми разработали PTAS-алгоритмы для задач поиска минимального времени завершения для взвешенной системы с указанием дат запуска. В таблице 1 приведено время выполнения этих PTAS-алгоритмов.

Результаты, представленные в таблице 1, были получены благодаря тщательному подбору последовательности преобразований на входе и последующему динамическому программированию. Преобразования на входе гарантируют, что входные данные будут иметь нужную структуру, за счет незначительного снижения оптимальности, а динамическое программирование обеспечивает эффективное перечисление всех почти оптимальных решений для хорошо структурированного экземпляра задачи.

Таблица 1. Основные результаты Афрати и др. [1]

Первым этапом преобразования на входе является геометрическое округление, при помощи которого длительность обработки и дата запуска преобразуются в степени значения [math]\displaystyle{ 1 + \epsilon \; }[/math], в результате чего общая эффективность снижается не более чем на [math]\displaystyle{ 1 + \epsilon \; }[/math]. Что еще более важно, этот этап: (1) гарантирует небольшое количество различных значений длительности обработки и даты запуска; (2) позволяет разбивать время на геометрически возрастающие интервалы; и (3) выравнивает даты запуска относительно временных границ начала и конца интервалов. Все эти полезные свойства могут использоваться алгоритмом динамического программирования.

Вторым этапом преобразования на входе является растягивание по времени, во время которого к плану на всем его протяжении добавляются небольшие объемы времени простоя. Этот этап также увеличивает время завершения не более чем на [math]\displaystyle{ 1 + O (\epsilon) \; }[/math], однако он полезен для лучшей организации процесса планирования. В частности, если задание слишком велико (т. е. занимает большую часть интервала, в котором оно выполняется), его можно переместить во время простоя более позднего интервала, в котором оно будет занимать небольшую часть времени. Это гарантирует, что большинство заданий будут иметь небольшой размер по сравнению с продолжительностью интервала, в котором они выполняются, что значительно упрощает составление плана. Следующим этапом будет перемещение заданий. Рассмотрим разбиение временного интервала [math]\displaystyle{ [ 0, \infty ) \; }[/math] на интервалы формы [math]\displaystyle{ I_x = [(1 + \epsilon)^x,(l + \epsilon)^{x + 1}) \; }[/math] для целочисленных значений x. Этап перемещения заданий гарантирует, что существует почти субоптимальный план, в котором каждое задание j выполняется в пределах [math]\displaystyle{ O(log_{1 + \epsilon} (1 + \frac{1}{\epsilon})) \; }[/math] интервалов после rj. Он имеет следующее интересное свойство: если мы рассмотрим блоки интервалов [math]\displaystyle{ B_0, B_1, ..., \; }[/math] где каждый блок [math]\displaystyle{ B_i \; }[/math] содержит [math]\displaystyle{ O(log_{1 + \epsilon} (1 + \frac{1}{\epsilon})) \; }[/math] последовательных интервалов, то задание j, начинающееся в блоке [math]\displaystyle{ B_i \; }[/math], завершается в пределах следующего блока. Последующие этапы на фазе перемещения заданий гарантируют, что останется не слишком много больших заданий, распространяющихся на следующий блок; это обеспечивает эффективное осуществление динамического программирования.

Точное содержание этапов алгоритмов и их анализ довольно сложны; здесь приводится только их упрощенное схематическое представление. Подробнее об этом – в [1] и [3].

Применение

Многие задачи оптимизации в области параллельных вычислений и исследования операций можно сформулировать в виде задач планирования вычислительных машин. При введении отношений предшествования между задачами нахождение времени завершения для взвешенной системы может выступать в качестве более общей цели по сравнению с широко распространенным нахождением периода обработки, и потому оказывается важным.

Открытые вопросы

Одна из основных нерешенных задач в этой области заключается в улучшении коэффициентов аппроксимации для планирования заданий с отношениями предшествования на несвязанных или связанных машинах. Следующие задачи заслуживают отдельного упоминания. Наилучшим известным решением задачи [math]\displaystyle{ 1 | prec | \sum w_j C_j \; }[/math] является алгоритм 2-аппроксимации Холла и др. [8]; улучшение этого коэффициента остается главным открытым вопросом теории планирования. Задача [math]\displaystyle{ R | prec | \sum_j w_j C_j \; }[/math], в которой отношения предшествования формируют произвольный ациклический граф, также представляет высокую важность: единственные результаты были получены для случая, когда отношения предшествования формируют цепи [6] или деревья [10].

Также неисследованным остается направление неаппроксимируемости – имеется немало серьезных пробелов между известными гарантиями аппроксимации и коэффициентами сложности для различных классов задач. Например, известно, что задачи [math]\displaystyle{ R || \sum w_j C_j \; }[/math] и [math]\displaystyle{ R | r_j | \sum w_j C_j \; }[/math] являются сложно-аппроксимируемыми, однако лучшие известные алгоритмы, предложенные Скутеллой [11], имеют коэффициента аппроксимации 3/2 и 2, соответственно. Устранение этих пробелов представляет собой важную задачу.

См. также

• Минимизация продолжительности потока
• Списочное планирование
• Минимальная продолжительность потока
• Минимальный период обработки на несвязанных машинах

Литература

1. Afrati, F.N., Bampis, E., Chekuri, C., Karger, D.R., Kenyon, C., Khanna, S., Milis, I., Queyranne, M., Skutella, M., Stein, C., Sviridenko, M.: Approximation schemes for minimizing average weighted completion time with release dates. In: Proc. of Foundations of Computer Science, pp. 32-44 (1999)

2. Bruno, J.L., Coffman, E.G., Sethi, R.: Scheduling independent tasks to reduce mean finishing time. Commun. ACM 17, 382-387(1974)

3. Chekuri, C., Khanna, S.: Approximation algorithms for minimizing weighted completion time. In: J. Y-T. Leung (eds.) Handbook of Scheduling: Algorithms, Models, and Performance Analysis. CRC Press, Boca Raton (2004)

4. Chekuri, C., Motwani, R., Natarajan, B., Stein, C.: Approximation techniques for average completion time scheduling. SIAM J.Comput.31(1), 146-166(2001)

5. Goemans, M., Queyranne, M., Schulz, A., Skutella, M., Wang, Y.: Single machine scheduling with release dates. SIAM J. Discret. Math. 15,165-192(2002)

6. Goldberg, L.A., Paterson, M., Srinivasan, A., Sweedyk, E.: Better approximation guarantees for job-shop scheduling. SIAM J. Discret. Math. 14,67-92 (2001)

7. Graham, R.L., Lawler, E.L., Lenstra, J.K., Rinnooy Kan, A.H.G.: Optimization and approximation in deterministic sequencing and scheduling: a survey. Ann. Discret. Math. 5,287-326 (1979)

8. Hall, L.A., Schulz, A.S., Shmoys, D.B., Wein, J.: Scheduling to minimize average completion time: off-line and on-line approximation algorithms. Math. Oper. Res. 22(3), 513-544 (1997)

9. Horn, W.: Minimizing average flow time with parallel machines. Oper. Res. 21,846-847 (1973)

10. Kumar, V.S.A., Marathe, M.V., Parthasarathy, S., Srinivasan, A.: Scheduling on unrelated machines under tree-like precedence constraints. In: APPROX-RANDOM, pp. 146-157(2005)

11. Skutella, M.: Convex quadratic and semi-definite relaxations in scheduling. J.ACM 46(2), 206-242 (2001)

12. Skutella, M., Woeginger, G.J.: A PTAS for minimizing the weighted sum of job completion times on parallel machines. In: Proc. of 31st Annual ACM Symposium on Theory of Computing (STOC'99), pp. 400^07 (1999)

13. Smith, W.E.: Various optimizers for single-stage production. Nav. Res. Log. Q. 3, pp. 59-66 (1956)