Дерево максимальной совместимости

Ключевые слова и синонимы

Поддерево максимальной уточненности (MRST)

Постановка задачи

Представляет собой задачу сопоставления с образцом для деревьев с помеченными листьями. Каждое дерево на входе рассматривается как образец ветвления, порождающий конкретную группу листьев. Пусть имеется набор деревьев с идентичными множествами листьев; необходимо найти максимальное подмножество листьев по образцу ветвления, на котором входные деревья совпадают. Дерево максимальной совместимости – это дерево, содержащее такой набор листьев и включающее образцы ветвления входных деревьев для этих листьев. Задача нахождения дерева максимальной совместимости (maximum compatible problem, MCP) заключается в нахождении такого дерева или, что эквивалентно, его набора листьев. Больше всего решение этой задачи необходимо в филогенетике – для измерения сходства между эволюционными деревьями или для формирования консенсуса для множества деревьев. Впервые задача была поставлена в [9] и [10] под названием MRST (поддерево максимальной уточненности). Предыдущие работы рассматривали хорошо известную задачу нахождения поддерева максимального соответствия (maximum agreement subtree, MAST). Решением MAST будет нахождение наибольшего подмножества листьев, на котором все входные деревья точно совпадают. Более точно, алгоритм MAST ищет дерево, у которого схема ветвления изоморфна схеме поддерева каждого из входных деревьев, тогда как MCT ищет дерево, содержащее схему ветвления (т.е. группы) поддерева каждого входного дерева. В результате дерево, полученное по алгоритму MCT, оказывается более информативным, поскольку оно может содержать схему ветвления, представленную только в одном из деревьев, если она не противоречит остальным деревьям. Если все входные деревья являются бинарными, эти задачи эквивалентны. Ганапати и Уорноу [5] первыми предложили алгоритм для решения задачи MCT в общем виде. Алгоритм работает на базе простого динамического подхода, близкого к используемому при решении MAST [12], и имеет время исполнения, экспоненциальное относительно количества входных деревьев и максимальной степени вершин входных деревьев. Позднее в [2] был предложен алгоритм с фиксированными параметрами, использующий только один параметр. Также были получены приближенные результаты [1, 6] – недорогие алгоритмы с полиномиальным временем исполнения, аппроксимирующие дополнение задачи MCT с константным порогом.

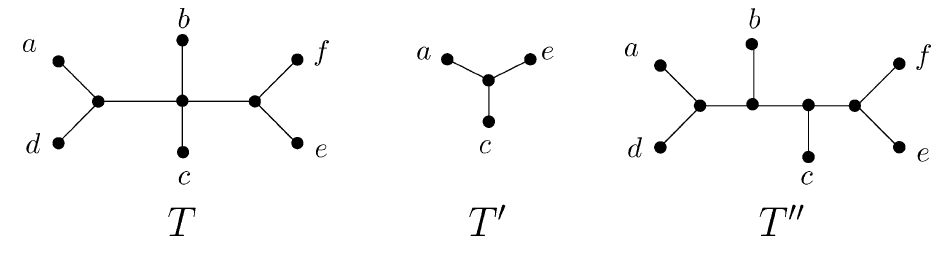
Дерево максимальной совместимости, рис. 1

Три некорневых дерева: дерево T; дерево T’, такое, что T’ = T | {a, c, e}; дерево T’’, такое, что T’’ [math]\displaystyle{ \trianglerighteq }[/math] T

Нотация

Деревья, которые здесь рассматриваются, представляют собой эволюционные (филогенетические) деревья. Такое дерево T имеет множество листьев L(T), находящихся во взаимно-однозначном соответствии с множеством меток, и является либо корневым (в этом случае все внутренние вершины имеют не менее двух потомков), либо некорневым (в этом случае внутренние вершины имеют степень не ниже трех). Размером |T| дерева T является число его листьев. Пусть дано множество меток L и дерево T; [топологическое] ограничение T согласно L, обозначаемое T|L, представляет собой дерево, полученное следующим образом: взять наименьший порожденный подграф T, соединяющий листья с метками из [math]\displaystyle{ L \cap L(T) \; }[/math], а затем удалить две некорневых вершины любой степени, чтобы дерево стало гомеоморфно неприводимым. Два дерева T и T' являются изоморфными (T = T') в том и только том случае, если существует изоморфизм графов [math]\displaystyle{ T \mapsto T' \; }[/math], сохраняющий метки листьев (и корень, если оба дерева были корневыми). Дерево T уточняет дерево T' ([math]\displaystyle{ T \trianglerighteq T' \; }[/math]), если T может быть преобразовано в T путем коллапсирования некоторых его внутренних ребер (под коллапсированием ребра понимается его удаление и слияние его конечных точек). На рис. 1 приведены примеры таких отношений между деревьями.

Отметим, что дерево T, должным образом уточняющее дерево T', согласуется со всей эволюционной историей T', но при этом содержит дополнительную информацию, отсутствующую в T': по меньшей мере одна вершина высокой степени из T заменяется в T несколькими вершинами меньших степеней, следовательно, T содержит больше событий видообразования, чем T'. Пусть имеется набор [math]\displaystyle{ \mathcal{T} = {T_1, T_2, ..., T_k} \; }[/math] входных деревьев с идентичными множествами листьев L. Мы говорим, что дерево T с листьями из L совместимо с [math]\displaystyle{ \mathcal{T} \; }[/math] в том и только том случае, если [math]\displaystyle{ \forall \mathcal{T}_i \in \mathcal{T}, T \trianglerighteq T_i|L(T) \; }[/math]. Если существует дерево [math]\displaystyle{ \mathcal{T} \; }[/math], совместимое с T, такое, что L(T) = L, то набор T называется совместимым. Для решения вопроса, является ли набор деревьев совместимым, давно известны линейные алгоритмы (см., например, в [8]). Задача нахождения дерева максимальной совместимости представляет собой вариант естественной оптимизации данной задачи, позволяющий обрабатывать наборы несовместимых деревьев.

Задача 1. Дерево максимальной совместимости (MCT)

Дано: набор деревьев [math]\displaystyle{ \mathcal{T} \; }[/math] с идентичными множествами листьев.

Требуется: найти дерево, совместимое с [math]\displaystyle{ \mathcal{T} \; }[/math], с наибольшим числом листьев. Такое дерево обозначается [math]\displaystyle{ MCT(\mathcal{T}) \; }[/math], его пример приведен на рис. 2.

Заметим, что [math]\displaystyle{ \forall \mathcal{T}, |MCT(\mathcal{T})| \ge |MAST(\mathcal{T})| \; }[/math], и MCT эквивалентно MAST в случае, если входные деревья являются бинарными. Также стоит отметить, что задачи MCT и MAST имеют несколько оптимальных решений.

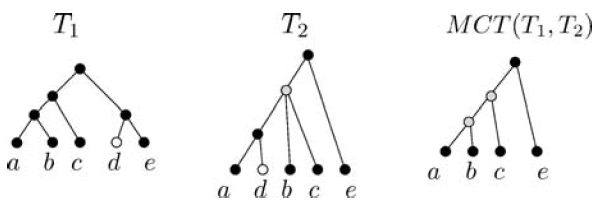
Дерево максимальной совместимости, рис. 2

Набор из двух несовместимых входных деревьев [math]\displaystyle{ {T_1, T_2} \; }[/math] и их дерево максимальной совместимости [math]\displaystyle{ T = MCT(T_1, T_2) \; }[/math]. Если удалить лист d, входные деревья станут совместимыми, поскольку L(Т) = {a, b, c, d}. Здесь дерево T строго уточняет [math]\displaystyle{ T_2\; }[/math] , ограниченное согласно L(T), что выражается тем обстоятельством, что потомки вершины дерева [math]\displaystyle{ T_2 \; }[/math] (изображенной серым цветом) распределены между несколькими связанными вершинами T (также серого цвета). Отметим также, что [math]\displaystyle{ |MCT(T_1, T_2)| \gt |MAST(T_1, T_2)| \; }[/math].

Основные результаты

Точные алгоритмы

Было показано, что задача MCT является NP-полной для 6 деревьев ([9]) и для 2 деревьев [10]. NP-полнота появляется, когда по меньшей мере одно из входных деревьев имеет неограниченную степень. Для случая двух деревьев с ограниченной степенью Хайн и коллеги упоминают алгоритм с полиномиальным временем исполнения, основанный на выравнивании деревьев [10]. Ганапати и Уорноу [5] предложили экспоненциальный алгоритм для решения задачи MCT в общем виде. Они показали, как для двух деревьев [math]\displaystyle{ T_1, T_2 \; }[/math] вычислить бинарное дерево MCT для любой пары поддеревьев [math]\displaystyle{ (S_1 \in T_1, S_2 \in T_2) \; }[/math] при помощи динамических алгоритмов. Поддеревья, корни которых имеют высокую степень, обрабатываются путем рассмотрения каждого возможного разбиения потомков корня на два множества. Из-за этого в оценке сложности появляется экспоненциальный терм относительно d – максимальной степени вершин входных деревьев. Если имеются k входных деревьев, то рассматриваются кортежи из k поддеревьев и производится подобное же разбиение потомков корневых вершин на два множества для k поддеревьев. Следовательно, сложность по-прежнему является экспоненциальной относительно k.

Теорема 1 ([5]). Пусть L – множество, содержащее n листьев. Задача MCT для набора из k корневых деревьев с листьями из L, в котором каждое дерево имеет степень не выше d + 1, может быть решена за время [math]\displaystyle{ O(2^{2kd} n^k) \; }[/math].

Результат можно легко расширить на некорневые деревья, если рассматривать каждый из n листьев как возможный корень для всех деревьев набора.

Теорема 2 ([5]). Пусть дан набор из k некорневых деревьев, степени которых не превышают d + 1, с множеством листьев мощности n. Тогда задача MCT может быть решена за время [math]\displaystyle{ O(2^{2kd} n^{k+1}) \; }[/math].

Пусть [math]\displaystyle{ \mathcal{T} \; }[/math] – набор деревьев с листьями из множества L. В работе [2] рассматривалась следующая задача, названная [math]\displaystyle{ MCT_p \; }[/math]: пусть даны [math]\displaystyle{ \mathcal{T} \; }[/math] и [math]\displaystyle{ p \in [0, n] \; }[/math]; верно ли, что [math]\displaystyle{ |MCT(\mathcal{T})j| \ge n - p \; }[/math]?

Теорема 3 ([2]).

1. Задача [math]\displaystyle{ MCT_p \; }[/math] для корневых деревьев может быть решена за время [math]\displaystyle{ O(min \{ 3^p kn, 2.27^p + kn^3 \}) \; }[/math].

2. Задача [math]\displaystyle{ MCT_p \; }[/math] для некорневых деревьев может быть решена за время [math]\displaystyle{ O \big( (p + 1) \times min \{ 3^p kn, 2.27^p + kn^3 \} \big) \; }[/math].

Терм [math]\displaystyle{ 3^p kn \; }[/math] возникает из-за использования алгоритма, который вначале за время O(kn) локализует множество S из трех листьев, на котором входные деревья конфликтуют, а затем рекурсивным образом вычисляет деревья максимальной совместимости [math]\displaystyle{ T_1 \; }[/math], [math]\displaystyle{ T_2 \; }[/math] и [math]\displaystyle{ T_3 \; }[/math] для каждого из трех наборов [math]\displaystyle{ \mathcal{T}_1 \; }[/math], [math]\displaystyle{ \mathcal{T}_2 \; }[/math] и [math]\displaystyle{ \mathcal{T}_3 \; }[/math], соответственно, полученных посредством удаления принадлежащего S листа из входных деревьев, и затем возвращает [math]\displaystyle{ T_i \; }[/math], такое, что [math]\displaystyle{ |T_i| \; }[/math] максимально (для [math]\displaystyle{ i \in [1, 3] \; }[/math]). Терм [math]\displaystyle{ 2.27^p + kn^3 \; }[/math] появляется из-за использования алгоритма, выполняющего редукцию MCT до 3-HITTING SET. Гийемо и Николя получили отрицательный результат при рассмотрении возможности разрешимости MCT с фиксированными параметрами для входных деревьев степени не выше D.

Теорема 4 ([7]).

1. MCT является W[1]-полной относительно D.

2. MCT не может быть решена за время [math]\displaystyle{ O(N^{o(2^{D/2})}) \; }[/math], если только не выполняется [math]\displaystyle{ SNP \subseteq SE \; }[/math], где N обозначает длину входных элементов, т.е. N = O(kn).

Задача MCT также предполагает вариант для супердеревьев, то есть деревьев, имеющих различные, но перекрывающиеся наборы листьев. В этом варианте задача является W[2]-полной относительно top[3].

Алгоритмы аппроксимации

Идея локализации и последующего успешного удаления всех конфликтов между входными деревьями также привела к созданию алгоритмов аппроксимации для дополнения задачи MCT, обозначаемого CMCT. Пусть L – множество листьев каждого дерева входного набора T. Целью задачи CMCT является выбор наименьшего числа листьев [math]\displaystyle{ S \subseteq I \; }[/math], таких, что набор [math]\displaystyle{ \{ T_i | (L - S): T_i \in \mathcal{T} \} \; }[/math] является совместимым.

Теорема 5 ([6]). Пусть дан набор [math]\displaystyle{ \mathcal{T} \; }[/math] из k корневых деревьев с множеством листьев L мощности n. Тогда существует алгоритм 3-аппроксимации задачи MCT с временем исполнения [math]\displaystyle{ O(k^2 n^2) \; }[/math].

Время исполнения этого алгоритма позднее было улучшено:

Теорема 6 ([1]). Существует алгоритм 3-аппроксимации с временем исполнения [math]\displaystyle{ O(kn + n^2) \; }[/math] для решения задачи CMCT на наборе k корневых деревьев с n листьев.

Отметим, что достижимый порог аппроксимации для CMCT не меняется в зависимости от того, рассматриваются ли корневые или некорневые деревья [1].

Применение

В биоинформатике алгоритм MCT (также как и MAST) используется для решения различных практических задач. Первая из них заключается в измерении схожести набора деревьев. Эти деревья могут представлять вторичные структуры РНК [10, 11] или предположительные схемы филогенеза, унаследованные от различных наборов данных, созданных из молекулярных последовательностей (например, генов) [13]. Разрыв между размером дерева максимальной совместимости и общим количеством входных листьев отражает степень несхожести входных деревьев. Если говорить о филогенетических приложениях, нередко случается, что некоторые ребра деревьев, полученных из наборов данных, оказываются сколлапсированными из-за недостаточной статистической поддержки, что приводит к образованию в рассматриваемых деревьях вершин более высоких степеней. Каждая подобная вершина обозначает не событие видообразования для нескольких видов, а только уровень неопределенности относительно того, какую схему ветвления следует выбрать для поддеревьев-потомков этой вершины. В таких случаях алгоритм MCT предпочтительнее MAST, поскольку первый корректно обрабатывает вершины высоких степеней, позволяя разрешать их в соответствии с информацией о ветвлении, представленной в других входных деревьях. В результате в выходном дереве сохраняется больше листьев, а значит, обнаруживается большая степень схожести входных деревьев. Отметим также, что низкая степень схожести между входными деревьями может возникать в силу горизонтального переноса генов. Подобные события происходят нечасто; определить виды, подверженные такому эффекту, можно, если вначале рассматривать листья, исключенные из дерева максимальной совместимости.

Форма дерева максимальной совместимости (а не только его размер) также находит применение в систематической биологии, позволяя обнаружить консенсус на наборе филогенетических деревьев, оптимальный согласно некоторому критерию формирования деревьев. К примеру, такие критерии, как максимальная экономичность и максимальное правдоподобие, могут привести к созданию нескольких десятков, а то и сотен, оптимальных и почти оптимальных деревьев. На практике такие деревья вначале группируются в островки соседних деревьев, для каждого островка формируется дерево-консенсус при помощи классического метода формирования консенсуса – например, правила большинства или строгого консенсуса. Деревья, представляющие островки, образуют набор, для которого затем ищется консенсус. Однако методы формирования консенсуса, стремящиеся сохранить все входные листья, создают деревья, которым недостает разрешения. Альтернативный подход заключается в формировании репрезентативного дерева, содержащего максимальное подмножество листьев в позициях, по которым входные деревья совпадают. В этом случае MCT также подходит больше, чем MAST, поскольку входные деревья могут содержать вершины высоких степеней того же типа, что описаны выше.

Открытые вопросы

В будущем имеет смысл изучение варианта алгоритма MCT, в котором некоторые листья обязательно должны быть представлены в выходном дереве. Эта проблема появляется тогда, когда биологи хотят, чтобы определенные виды, занимающие важное место в их исследовании, обязательно содержались в выходном дереве. Для задачи MAST на двух деревьях этот вариант с ограничениями показал такую же сложность, как и стандартный вариант [4]. Однако для MCT подобное ограничение может быть связано с решением нескольких проблем оптимизации. Еще одна необходимая работа – это серия экспериментов по измерению диапазона параметров, для которых окажутся полезными алгоритмы точного или приближенного решения задачи MCT.

См. также

• Поддерево максимального соответствия (для двух бинарных деревьев)
• Поддерево максимального соответствия (для трех или более деревьев)

Литература

1. Berry, V., Guillemot, S., Nicolas, F., Paul, C.: On the approximation of computing evolutionary trees. In: Wang, L. (ed.) Proc. of the 11th Annual International Conference on Computing and Combinatorics (COCOON'05). LNCS, vol. 3595, pp. 115-125. Springer, Berlin (2005)

2. Berry, V., Nicolas, F.: Improved parametrized complexity of the maximum agreement subtree and maximum compatible tree problems. IEEE/ACM Trans. Comput. Biol. Bioinform. 3(3), 289-302 (2006)

3. Berry, V., Nicolas, F.: Maximum agreement and compatible supertrees. J. Discret. Algorithms. Algorithmica, Springer, New York (2008)

4. Berry, V., Peng, Z.S., Ting, H.-F.: From constrained to unconstrained maximum agreement subtree in linear time. Algorithmica, to appear (2006)

5. Ganapathy, G., Warnow, T.J.: Finding a maximum compatible tree for a bounded number of trees with bounded degree is solvable in polynomial time. In: Gascuel, O., Moret, B.M.E. (eds.) Proc. of the 1st International Workshop on Algorithms in Bioinformatics (WABI'01), pp. 156-163 (2001)

6. Ganapathy, G., Warnow, T.J.: Approximating the complement of the maximum compatible subset of leaves of k trees. In: Proc. of the 5th International Workshop on Approximation Algorithms for Combinatorial Optimization (APPROX'02), LCNS, vol. 2462, pp. 122-134., Springer, Berlin (2002)

7. Guillemot, S., Nicolas, F.: Solving the maximum agreement subtree and the maximum compatible tree problems on many bounded degree trees. In: Lewenshtein, M., Valiente, G. (eds.) Proc. of the 17th Combinatorial Pattern Matching Symposium (CPM'06). LNCS, vol.4009, pp. 165-176. Springer, Berlin (2006)

8. Gusfield, D.: Efficient algorithms for inferring evolutionary trees. Networks 21,19-28 (1991)

9. Hamel, A.M., Steel, M.A.: Finding a maximum compatible tree is NP-hard for sequences and trees. Appl. Math. Lett. 9(2), 55-59(1996)

10. Hein, J., Jiang, T., Wang, L., Zhang, K.: On the complexity of comparing evolutionary trees. Discrete Appl. Math. 71(1-3), 153-169(1996)

11. Jiang, T., Wang, L., Zhang, K.: Alignment of trees - an alternative to tree edit. Theor. Comput. Sci. 143(1), 137-148 (1995)

12. Steel, M.A., Warnow, T.J.: Kaikoura tree theorems: Computing the maximum agreement subtree. Inform. Process. Lett. 48(2), 77-82(1993)

13. Swofford, D.L., Olsen, G.J., Wadell, P.J., Hillis, D.M.: Phylogenetic inference. In: Hillis, D.M., Moritz, D.M., Mable, B.K. (eds.) Molecular systematics, 2nd edn. pp.407-514. Sunderland, USA (1996)