Самодополнительный граф: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Самодополнительный граф''' (''Self-complementary graph'') - граф, изоморфный своему допо...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
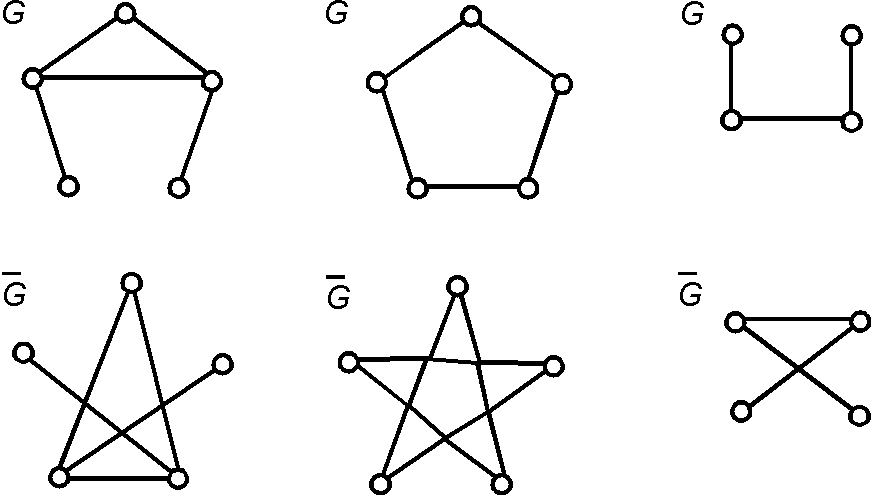
'''Самодополнительный граф''' (''Self-complementary graph'') | '''Самодополнительный граф''' (''[[Self-complementary graph]]'') — | ||
граф, изоморфный своему дополнению. | [[граф]], [[изоморфизм графов|изоморфный]] своему [[дополнение графа|дополнению]]. | ||
[[Файл:Self-complementary graph.png|600px]] | |||
Самодополнительными графами | Самодополнительными графами | ||
являются, например, 4-вершинная простая цепь и 5-вершинный простой | являются, например, 4-вершинная [[простая цепь]] и 5-вершинный [[простой цикл]]. | ||
цикл. | |||
==Литература== | ==Литература== | ||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
* Харари Ф., Палмер Э. Перечисление графов. — М.: Мир,1977. | |||
Текущая версия от 12:44, 1 сентября 2011
Самодополнительный граф (Self-complementary graph) — граф, изоморфный своему дополнению.
Самодополнительными графами являются, например, 4-вершинная простая цепь и 5-вершинный простой цикл.
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.
- Харари Ф., Палмер Э. Перечисление графов. — М.: Мир,1977.