N-Нумерация: различия между версиями
Glk (обсуждение | вклад) (Создана новая страница размером '''N-Нумерация''' (''N-Numbering'') - для данной <math>M</math>-''нумерации'' такая нумерация <...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''N-Нумерация''' (''N-Numbering'') | '''<math>\,N</math>-Нумерация''' (''[[N-Numbering|<math>\,N</math>-Numbering]]'') — | ||
для данной | для данной | ||
<math>M</math>-''нумерации'' такая нумерация <math>N</math> вершин, что для любых вершин <math>a</math> и | [[M-Нумерация|<math>\,M</math>-''нумерации'']] такая [[нумерация вершин|нумерация <math>\,N</math> вершин]], что для любых вершин <math>\,a</math> и | ||
<math>b</math> неравенство <math>N(a) < N(b)</math> выполняется тогда и только тогда, когда | <math>\,b</math> неравенство <math>\,N(a) < N(b)</math> выполняется тогда и только тогда, когда | ||
либо вершина <math>b</math> <math>M</math>-достижима из <math>a</math> | либо [[вершина]] <math>\,b</math> <math>\,M</math>-[[достижимая вершина|достижима]] из <math>\,a,</math> либо <math>\,M(b) < M(a)</math> и вершина <math>\,a</math> | ||
не является <math>M</math>-достижимой из <math>b</math> | не является <math>\,M</math>-достижимой из <math>\,b.</math> | ||
Вместе с <math>M</math>-нумерацией образуют | Вместе с <math>\,M</math>-нумерацией образуют | ||
пару ''базисных нумераций''. | пару ''[[базисная нумерация|базисных нумераций]]''. | ||
Другое название | [[Файл:N-Numbering.png|700px]] | ||
Другое название — ''[[Обратная нумерация]]''. | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
Текущая версия от 05:04, 20 мая 2011
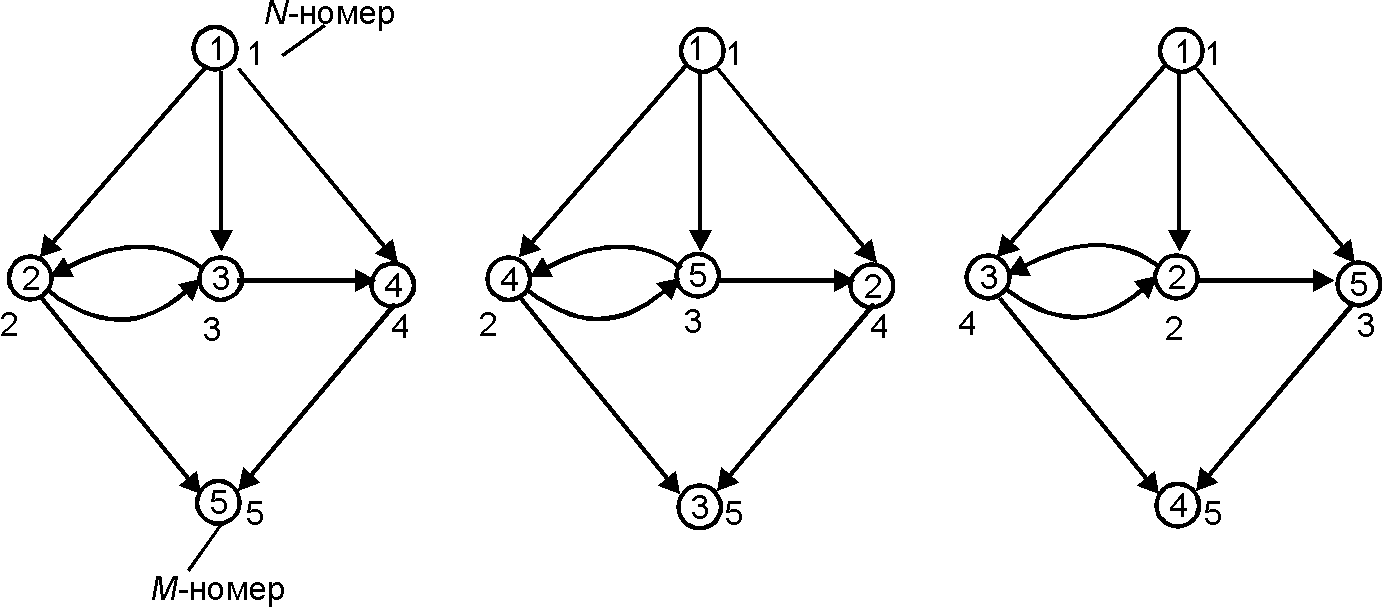
[math]\displaystyle{ \,N }[/math]-Нумерация ([math]\displaystyle{ \,N }[/math]-Numbering) — для данной [math]\displaystyle{ \,M }[/math]-нумерации такая нумерация [math]\displaystyle{ \,N }[/math] вершин, что для любых вершин [math]\displaystyle{ \,a }[/math] и [math]\displaystyle{ \,b }[/math] неравенство [math]\displaystyle{ \,N(a) \lt N(b) }[/math] выполняется тогда и только тогда, когда либо вершина [math]\displaystyle{ \,b }[/math] [math]\displaystyle{ \,M }[/math]-достижима из [math]\displaystyle{ \,a, }[/math] либо [math]\displaystyle{ \,M(b) \lt M(a) }[/math] и вершина [math]\displaystyle{ \,a }[/math] не является [math]\displaystyle{ \,M }[/math]-достижимой из [math]\displaystyle{ \,b. }[/math] Вместе с [math]\displaystyle{ \,M }[/math]-нумерацией образуют пару базисных нумераций.
Другое название — Обратная нумерация.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.