BB-Дерево: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''<math>BB</math>-Дерево''' (''<math>BB</math>-Tree'') - дерево <math>T_{n} \, = \, (T_{l}, r, T_{r})</math>с корнем ...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 4 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''<math>BB</math>-Дерево''' (''<math>BB</math>-Tree'') | [[Файл:BB-Tree.png|300px|right]] | ||
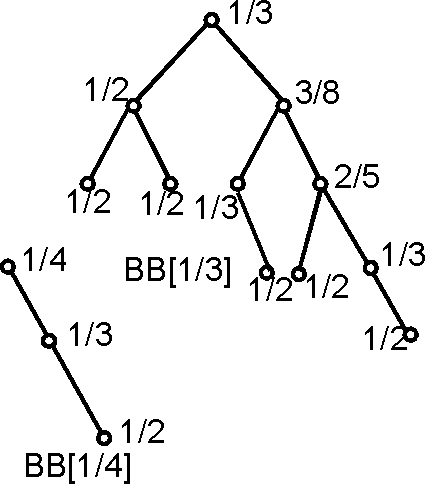
дерево <math>T_{n} \, = \, (T_{l}, r, T_{r})</math>с корнем <math>r</math> называется | '''<math>BB</math>-Дерево''' (''[[BB-Tree|<math>BB</math>-Tree]]'') — [[дерево]] <math>T_{n} \, = \, (T_{l}, r, T_{r})</math> с [[корень|корнем]] <math>r</math> называется <math>BB</math>-деревом с балансом <math>\alpha</math>, <math>0 \leq \alpha \leq 1/2</math>, если: | ||
<math>BB</math>-деревом с балансом <math>\alpha</math>, <math>0 \leq \alpha \leq 1/2</math>, если: | |||
а) для ''корневого баланса'' <math>\rho(T_{n})</math> выполняется условие | а) для ''корневого баланса'' <math>\rho(T_{n})</math> выполняется условие <math>\alpha \leq \rho(T_{n}) \leq 1-\alpha</math>; | ||
<math>\alpha \leq \rho(T_{n}) \leq 1-\alpha</math>; | |||
б) <math>T_{l}</math>и <math>T_{r}</math> | б) <math>T_{l}</math> и <math>T_{r}</math> — <math>BB</math>-деревья с балансом <math>\alpha</math>. | ||
Другое название | |||
Другое название — ''[[Балансированное по весу дерево]]''. | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. | |||
Текущая версия от 05:59, 4 февраля 2011
[math]\displaystyle{ BB }[/math]-Дерево ([math]\displaystyle{ BB }[/math]-Tree) — дерево [math]\displaystyle{ T_{n} \, = \, (T_{l}, r, T_{r}) }[/math] с корнем [math]\displaystyle{ r }[/math] называется [math]\displaystyle{ BB }[/math]-деревом с балансом [math]\displaystyle{ \alpha }[/math], [math]\displaystyle{ 0 \leq \alpha \leq 1/2 }[/math], если:
а) для корневого баланса [math]\displaystyle{ \rho(T_{n}) }[/math] выполняется условие [math]\displaystyle{ \alpha \leq \rho(T_{n}) \leq 1-\alpha }[/math];
б) [math]\displaystyle{ T_{l} }[/math] и [math]\displaystyle{ T_{r} }[/math] — [math]\displaystyle{ BB }[/math]-деревья с балансом [math]\displaystyle{ \alpha }[/math].
Другое название — Балансированное по весу дерево.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980.