Гамак: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Гамак''' ([[Hammock]]) | [[Файл:Hammock.png|300px|right]] | ||
'''Гамак''' (''[[Hammock]]'') — [[альт]], множество [[Конечная вершина Фрагмента|конечных]] вершин которого либо пусто, либо состоит из единственной вершины, являющейся преемником каждой [[Выходная вершина Фрагмента|выходной]] вершины [[Альт|альта]] и не являющейся [[Предшественник вершины|предшественником]] | |||
его [[Начальная вершина Фрагмента|начальной]] вершины. | его [[Начальная вершина Фрагмента|начальной]] вершины. | ||
| Строка 10: | Строка 11: | ||
== См. также == | == См. также == | ||
[[Иерархия вложенных альтов]]. | * [[Иерархия вложенных альтов]]. | ||
== Литература == | == Литература == | ||
* Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
Текущая версия от 05:56, 2 декабря 2010
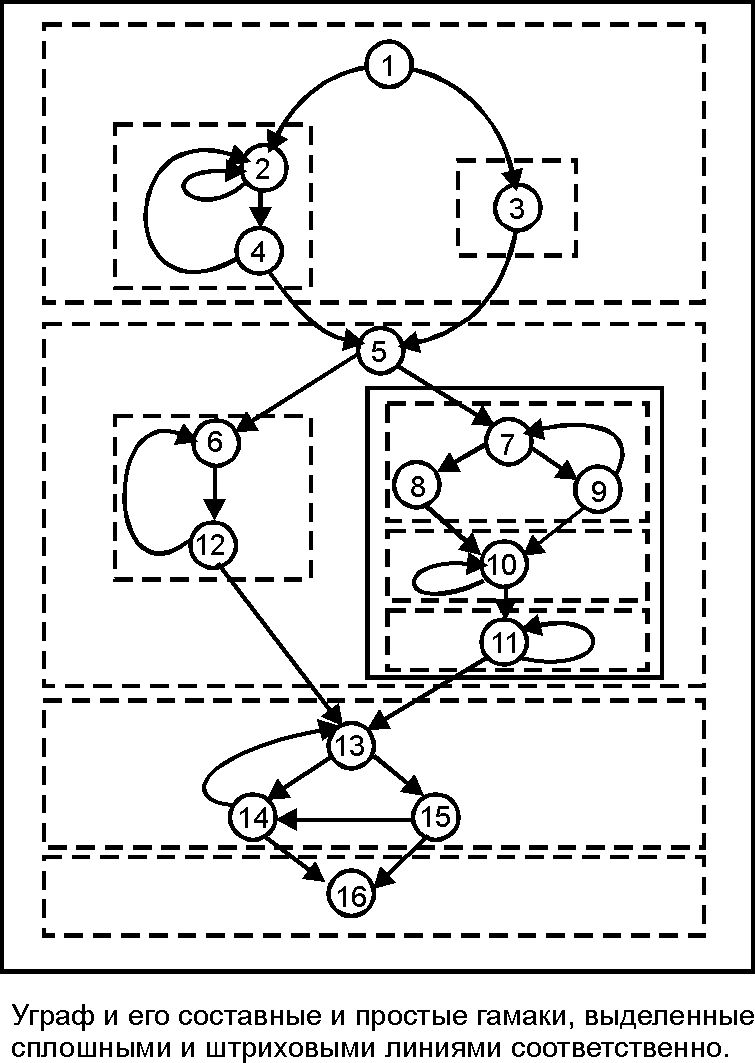
Гамак (Hammock) — альт, множество конечных вершин которого либо пусто, либо состоит из единственной вершины, являющейся преемником каждой выходной вершины альта и не являющейся предшественником его начальной вершины.
Гамак называется разложимым, если его можно представить как объединение двух непересекающихся гамаков, и неразложимым (или простым) в противном случае. Максимальный разложимый гамак называется составным.
См. также
Литература
- Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.