Бивершина: различия между версиями
Материал из WEGA
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
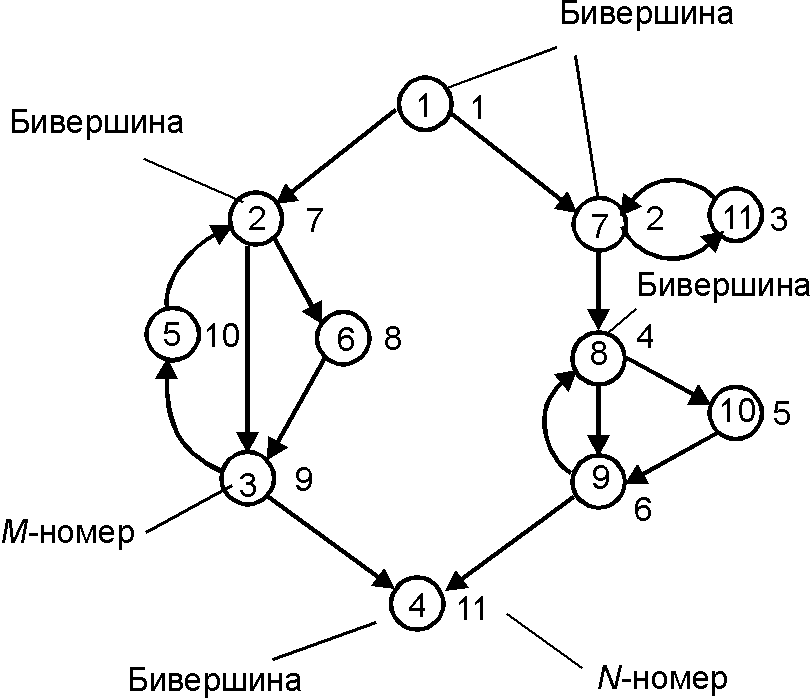
'''Бивершина''' (''[[Binode]]'') | '''Бивершина''' (''[[Binode]]'') — для фиксированных ''[[базисная нумерация|базисных нумераций]]'' <math>M</math> и <math>N</math> такая [[вершина]] <math>v</math>, что для любого индекса <math>i < N(v)</math> она принадлежит <math>N</math>-''области'' <math>N[i]</math>. Каждой [[бикомпонента|бикомпоненте]] графа соответствует в заданной <math>N</math>-нумерации ровно одна бивершина — та из вершин бикомпоненты, которая имеет наименьший <math>N</math>-номер. | ||
[[Файл:Binode.png|500px]] | |||
==Литература== | ==Литература== | ||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
* Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985. | |||
Текущая версия от 08:47, 19 ноября 2010
Бивершина (Binode) — для фиксированных базисных нумераций [math]\displaystyle{ M }[/math] и [math]\displaystyle{ N }[/math] такая вершина [math]\displaystyle{ v }[/math], что для любого индекса [math]\displaystyle{ i \lt N(v) }[/math] она принадлежит [math]\displaystyle{ N }[/math]-области [math]\displaystyle{ N[i] }[/math]. Каждой бикомпоненте графа соответствует в заданной [math]\displaystyle{ N }[/math]-нумерации ровно одна бивершина — та из вершин бикомпоненты, которая имеет наименьший [math]\displaystyle{ N }[/math]-номер.
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985.