Остовное дерево с максимальным количеством листьев: различия между версиями
Irina (обсуждение | вклад) Нет описания правки |
KVN (обсуждение | вклад) |
||
| (не показаны 33 промежуточные версии 1 участника) | |||
| Строка 4: | Строка 4: | ||
== Постановка задачи == | == Постановка задачи == | ||
Задача построения | Задача построения остовного дерева с максимальным количеством листьев (ОДМЛ; MAX LEAF SPANNING TREE) заключается в нахождении [[остовное дерево|остовного дерева]], имеющего не менее k листьев, в неориентированном графе. Версия разрешимости для параметризованной задачи построения ОДМЛ выглядит следующим образом: | ||
| Строка 11: | Строка 11: | ||
Параметр: целое число k. | Параметр: целое число k. | ||
Вопрос: имеет ли граф G с не менее чем k листьями? | Вопрос: имеет ли граф G остовное дерево с не менее чем k листьями? | ||
Параметризованная сложность недетерминированного алгоритма | Параметризованная сложность недетерминированного полного алгоритма ОДМЛ с полиномиальным временем выполнения широко изучалась [2, 3, 9, 11] с использованием кернелизации, ветвления и других техник с фиксированными параметрами (fixed-parameter tractable, FPT). Авторы работы [8] первыми предложили метод на базе экстремальной структуры для решения сложных вычислительных задач. Этот метод, выполненный в духе Гротендика и следующий в русле проекта миноров графов Робертсона и Сеймура, заключается в том, что математический проект развивается как серия небольших шагов, выполняемых по общей траектории, описываемой подходящей «математической машиной». Авторы подхода предпочитают высказывания следующего типа: каждый связный граф с n вершинами, удовлетворяющий определенному набору свойств, имеет остовное дерево с не менее чем k листьями, и это остовное дерево можно найти за время <math>O(f(k) + n^c) \;</math>, где c – константа (независимая от k), а f - произвольная функция. | ||
При рассмотрении параметризованной сложности значение k называется параметром, который | При рассмотрении параметризованной сложности значение k называется ''параметром'', который отражает некоторую структуру входных данных или другой аспект цели вычисления. Например, k может обозначать количество ребер, которые необходимо удалить для получения графа без циклов; количество последовательностей ДНК, подлежащих выравниванию в задаче выравнивания последовательностей; максимальную глубину вложенности объявления типа у компилятора; <math>k = 1 / \epsilon \;</math> может обозначать параметризацию при анализе аппроксимации; кроме того, k также может быть составным значением, зависящим от нескольких переменных. | ||
Существуют два основных способа сравнения FPT-алгоритмов, в результате чего появилось два класса FPT-задач. В классе «f(k)» задача заключается в поиске еще более медленно растущих функций от параметра f(k), управляющих сложностью FPT-алгоритмов. Класс «кернелизации» опирается на следующую лемму, утверждающую, что задача принадлежит к разряду FPT в том и только том случае, если входные данные могут быть предварительно обработаны (кернелизованы) за «обычное» полиномиальное время | Существуют два основных способа сравнения FPT-алгоритмов, в результате чего появилось два ''класса'' FPT-задач. В классе «f(k)» задача заключается в поиске еще более медленно растущих функций от параметра f(k), управляющих сложностью FPT-алгоритмов. Класс «кернелизации» опирается на следующую лемму, утверждающую, что задача принадлежит к разряду FPT-задач в том и только том случае, если входные данные могут быть предварительно обработаны ([[кернелизация|кернелизованы]]) за «обычное» полиномиальное время с получением экземпляра, размер которого ограничивается только функцией от k. | ||
Лемма 1. Параметризованная задача | '''Лемма 1.''' Параметризованная задача <math>\Pi \;</math> является задачей с фиксированными параметрами (FPT) в том и только том случае, если существует преобразование с полиномиальным временем выполнения (относительно n и k), переводящее (x, k) в (x', k'), такое, что: | ||
(1) (x, k) является «да-экземпляром» <math>\Pi \;</math> в том и только том случае, если (x', k') является «да-экземпляром» <math>\Pi \;</math>, | |||
(2) <math>k' \le k \;</math>, | |||
(3) <math>|x'| \le g(k) \;</math> для некоторой фиксированной функции g. | |||
В ситуации, описываемой леммой, предположим, что мы можем кернелизовать исходные экземпляры до экземпляров размером не более g(k). Два этих класса задач нередко бывают тесно связаны, однако результаты их выполнения различаются. Наилучший известный FPT-алгоритм задачи построения остовного дерева с максимальным количеством листьев с временем выполнения <math>O^* (8,12^k) \;</math> предложил Бонсма [1] на основе подхода на базе экстремальных структур, который разработали Эстивилл-Кастро, Феллоуз, Лэнгстон и Розамонд [8]. Этот алгоритм определяет, имеет ли граф G с n вершинами остовное дерево не менее чем с k листьями. В то же время авторы работы [8] представили FPT-алгоритм с наименьшим размером ядра. | |||
Можно выделить пять независимых объектов, связанных с теорией экстремальных структур и иллюстрирующих все цели алгоритма построения остовного дерева с максимальным количеством листьев. Перечислим эти пять целей: | |||
(а) Более эффективные FPT-алгоритмы, полученные в результате применения более глубокой теории структур, более мощных правил редукции, связанных с этой теорией, и более сильных доказательств по индукции для улучшенных границ кернелизации. | |||
(б) Правила мощной предварительной обработки ([[редукция данных|редукции данных]] / кернелизации) и комбинации правил, которые могут использоваться независимо от того, насколько мал параметр, и могут комбинироваться с другими подходами – например, аппроксимацией и эвристиками. Обычно они несложны для программирования. | |||
(в) Градиенты и правила преобразования для эвристик локального поиска. | (в) Градиенты и правила преобразования для эвристик локального поиска. | ||
(г) | |||
(г) Аппроксимационные алгоритмы с полиномиальным временем выполнения и границы эффективности, доказанные систематическим образом. | |||
(д) Структура, используемая для решения других задач. | (д) Структура, используемая для решения других задач. | ||
== Основные результаты == | == Основные результаты == | ||
Основным результатом является ''метод экстремальной структуры'', используемый в качестве системного подхода к разработке FPT-алгоритмов. Рассмотрим пять перечисленных выше взаимосвязанных целей, проиллюстрировав каждую при помощи данной задачи. | |||
'''Цель (а): FPT-алгоритмы''' | |||
Цель заключается в нахождении правил предварительной обработки (кернелизации) с полиномиальным временем выполнения, где g(k) насколько возможно мало. Это будет важно впоследствии в контексте цели (б). | |||
[[Файл:MLST_1.png]] | |||
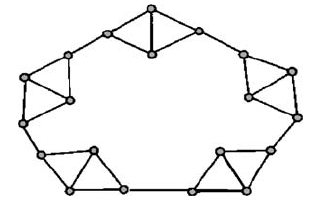
Рис. 1. Правила редукции были выведены для редукции данной структуры графа Клейтмана-Веста | |||
Если перефразировать задачу в терминах теории структур, важнейший вопрос будет звучать следующим образом: какова структура графов, не имеющих подграфа с k листьями? Результат Клейтмана и Веста из теории графов показывает, что граф с минимальной степенью не менее 3, не включающий подграф с k листьями, имеет не более 4(k - 3) вершин. На рис. 1 показано, что это лучший возможный результат для данной гипотезы. Однако исследование структуры при помощи экстремальных методов выявляет необходимость в применении правила редукции, показанного на рис. 2. Примерно двадцати различных правил редукции с полиномиальным временем выполнения (некоторые из них являются намного более сложными и «глобальными» по своей структуре, чем приведенное для примера простое локальное правило редукции) будет достаточно для кернелизации графа с минимальной степенью 2, имеющего не более 3,5k вершин. | |||
[[Файл:MLST_2.png]] | |||
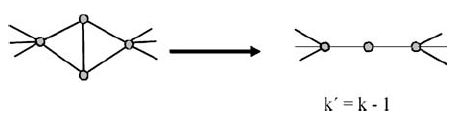
Рис. 2. Правило редукции для графа Клейтмана-Веста | |||
В общем случае экземпляр параметризованной задачи состоит из пары (x, k) и «границы», которая вычисляется посредством фиксации x и изменения k с последующим определением, какой ответ имеет [[задача разрешимости]] – «да» или «нет». Представляет интерес величина границы при редукции x. Типичная граничная лемма выглядит следующим образом. | |||
'''Лемма 2.''' Пусть (G, k) – экземпляр задачи построения остовного дерева с максимальным количеством листьев после редукции, для которого (G, k) является «да-экземпляром», а (G, k + 1) – «нет-экземпляром». Тогда <math>|G| \le ck \;</math> (где c – небольшая константа, значение которой будет вычислено в результате исследования). | |||
Доказательство граничной леммы выполняется при помощи минимального контрпримера. Контрпримером будет служить граф, такой, что (1) (G, k) – экземпляр задачи ОДМЛ после редукции; (2) (G, k) является «да-экземпляром»; (3) (G, k + 1) является «нет-экземпляром»; (4) |G| > ck. | |||
Доказательство граничной леммы будет производиться последовательным образом. Изначально неизвестно, при каком значении границы будет достигнут успех, а также точно неизвестно, что подразумевается под ''редукцией''. В ходе попытки доказательства эти аспекты станут ясны. По мере раскрытия аргументов особенности структуры подскажут формулировки новых правил редукции. При доказательстве граничной леммы необходимо будет принимать следующие стратегические решения: | |||
(1) Определение полярности границы и формулировка граничной леммы. | |||
(2) Выбор структуры-свидетеля. | |||
(3) Задание индуктивных приоритетов. | |||
(4) Разработка серии утверждений по поводу структуры, описывающих ситуацию на границе. | |||
(5) Определение правил редукции, выполняющихся за полиномиальное время над релевантными структурными ситуациями на границе. | |||
(6) По мере уточнения структуры на границе – заполнение неизвестных компонентов границы кернелизации. | |||
Общая структура аргумента вычисляется при помощи минимального контрпримера согласно приоритетам, заданным в результате выбора (3), который обычно ссылается на выбор (2). Доказательство развивается посредством серии небольших шагов, состоящих из утверждений по поводу структуры, которые в сумме ведут к получению детальной структурной картины на «границе» и, следовательно, позволяют определить границу размера G, которая и представляет собой заключение леммы. Полное доказательство объединяет серию утверждений по поводу дерева-свидетеля, различных множеств вершин и индуктивных приоритетов и формулирует основное неравенство, на основе которого производится доказательство по индукции, и ядро задачи размера 3,5k. | |||
'''Цель (б): предварительная обработка с полиномиальным временем выполнения и подпрограммы редукции данных''' | |||
Ниже приводится пример таблицы, используемой для отслеживания каждого возможного состояния границы для возможного решения. Можно привести примеры, демонстрирующие исключительно успешное каскадное применение правил редукции данных к реальным распределениям данных и описывающие разнообразие математических феноменов, относящихся к правилам редукции. Например, некоторые правила редукции – такие как ''правило разложения на составляющие Клейтмана-Веста'' для задачи ОДМЛ (рис. 2) – имеют фиксированный «размер границы» (в данном случае равный 2), тогда как правила редукции типа «корона» не имеют такового. | |||
'''Цель (в): градиенты и преобразования решений для локального поиска''' | |||
Здесь производится обобщение обычной формулировки для локального поиска, основанное на степени более сложного градиента в процессе получения более высоких границ кернелизации. Первая идея заключается в проведении локального поиска на основе поддержки «текущей структуры-свидетеля», а не полного решения (остовного дерева). Вторая идея состоит в использовании списка индуктивных приоритетов для определения градиента «лучшего решения» для локального поиска. | |||
'''Цель (г): аппроксимационные алгоритмы с полиномиальным временем выполнения''' | |||
Теория использования экстремальных структур с полиномиальным временем выполнения напрямую приводит к получению аппроксимационного алгоритма ОДМЛ с константным множителем и полиномиальным временем выполнения. Вначале выполним редукцию G при помощи правил кернелизации. Правила редукции сохраняют параметры аппроксимации. Возьмем любое дерево T (не обязательно остовное) в графе G. Если выполняются все утверждения касательно структуры, тогда (согласно рассуждениям граничной леммы) дерево T должно иметь не менее n/c листьев для c = 3,75. Таким образом, восстановив T с учетом произведенной редукции, получим c-аппроксимацию. | |||
Если по меньшей мере одно утверждение касательно структуры не выполняется, то дерево T можно улучшить, опираясь на один из индуктивных приоритетов. Заметим, что каждое утверждение доказывается посредством рассуждения, которое можно интерпретировать как подпрограмму улучшения T с полиномиальным временем выполнения в случае противоречия утверждению. | |||
Последовательность этих действий можно применить к исходному дереву T (и его потомкам) только полиномиальное количество раз, определяемое списком индуктивных приоритетов, до того момента, как мы получим дерево T', для которого выполняются все утверждения касательно структуры. В этот момент мы должны получить решение с c-аппроксимацией. | |||
'''Цель (д): структура, используемая для определения экологии сложности''' | |||
Цель заключается в том, чтобы понять, как именно каждый параметр, определяющий входные данные задачи, влияет на сложность всех других задач. В качестве примера рассмотрим таблицу 1: | |||
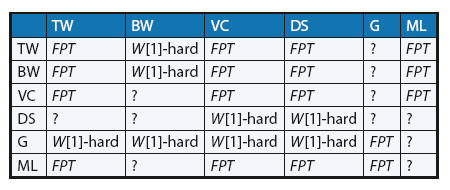
[[Файл:MLST_3.png]] | |||
Таблица 1. Экология сложности параметров | |||
Здесь используются следующие сокращения: TW – это древесная ширина дерева (TREEWIDTH), BW – ширина полосы (BANDWIDTH), VC – вершинное покрытие (VERTEX COVER), DS – доминирующее множество (DOMINATING SET), G – род (GENUS), а ML – максимальное количество листьев (MAX LEAF). Обозначение во второй строке и четвертом столбце говорит о том, что существует FPT-алгоритм для решения задачи DOMINATING SET на графе G с шириной полосы не более k. Обозначение в четвертой строке и втором столбце говорит о том, что неизвестно, может ли задача BANDWIDTH быть оптимально решена FPT-алгоритмом, если параметром является граница числа доминирования входного графа. | |||
MAX LEAF применяется к последней строке таблицы. Для графов с максимальным количеством листьев, ограниченным k, максимальный размер независимого множества может быть вычислен за время <math>O^* (2,972^k) \;</math> на основе редукции до ядра размером не более 7k. Использование результата решения одной задачи в качестве исходных данных для другой задачи оказывается весьма практичным. | |||
== Применение == | |||
Задача построения остовного дерева с максимальным количеством листьев применяется в расчетах компьютерной графики с целью создания представлений полосы треугольников для быстрого интерактивного рендеринга [5]. Также она находит применение в области перераспределения трафика и проектирования сетей – например, для проектирования оптических сетей и распределения используемых длин волн для снижения стоимости сети – в терминах оконечного оборудования либо электронных переключателей [6]. Задача о минимальной энергии в беспроводных сетях заключается в нахождении радиус-вектора передачи для всех станций таким образом, чтобы полная мощность излучения всей сети была насколько возможно малой. Ограниченная версия этой задачи эквивалентна задаче нахождения остовного дерева с максимальным количеством листьев [7]. Задача поиска остовных деревьев с большим числом листьев эквивалентна задаче поиска небольших связных доминирующих множеств и в связи с этим также носит название задачи о минимальном связном доминирующем множестве [13]. | |||
== Открытые вопросы == | |||
'''Стратегии ветвления''' | |||
Хотя экстремальные структуры в определенном смысле представляют собой правильный подход к разработке FPT-алгоритма, этот подход не единственный. В частности, он не дает ответа на вопрос, что делать с ядром. Остается открытым вопрос поиска общих стратегий использования «структурной теории с подходящими параметрами» в стратегиях ветвления при анализе ядер в сложных задачах. | |||
'''Кернелизуемость Тьюринга''' | |||
Преобразование с полиномиальным временем выполнения (x, k) к более простому редуцированному экземпляру (x', k') является преобразованием «от многих к одному». Можно обобщить понятие редукции «от многих к одному» до редукции Тьюринга. Как должен развиваться поиск экстремальных структур с полиномиальным временем выполнения в контексте такого менее жесткого FPT-алгоритма? | |||
'''Алгоритмические формы подхода на базе граничной леммы''' | |||
Из гипотезы граничной леммы о том, что (G, k) является «да-экземпляром», следует, что существует структура, являющаяся свидетелем для данного факта. Не делается предположений о том, что к этой структуре имеется алгоритмический доступ, а когда будут найдены правила редукции, они должны представлять собой преобразования, которые могут быть применены к (G, k) и структуре, которая может быть найдена в (G, k) за полиномиальное время. Иными словами, правила редукции не могут быть ''определены'' относительно структуры-свидетеля. Возможно ли описать более общие подходы к кернелизации, при которых структура-свидетель, используемая в ходе доказательства граничной леммы, может быть вычислена за полиномиальное время, и эта структура предоставит условный контекст для некоторых правил редукции? Как эти подходы изменят метод использования экстремальной структуры? | |||
'''Задача с аннотациями''' | |||
Можно рассмотреть обобщенную задачу построения остовного дерева с максимальным количеством листьев (MAX LEAF), в которой вершины и ребра имеют различные аннотации, говорящие о том, какие вершины ''должны'' быть листьями (или внутренними вершинами) в решении, и т.д. В общем случае подобная обобщенная форма задачи будет сложнее вышеописанной более простой формы. Однако некоторые из «наиболее известных» FPT-алгоритмов для решения различных задач основаны на таких обобщенных формах с аннотациями. В качестве примеров можно привести алгоритмы нахождения доминирующего множества для планарного графа (PLANAR DOMINATING SET) и разрывающего множества вершин (FEEDBACK VERTEX SET) [4]. Должны ли аннотации быть непременным компонентом рецепта наилучшего возможного алгоритма кернелизации с полиномиальным временем выполнения? | |||
== См. также == | |||
* ''[[Связное доминирующее множество]] | |||
* ''[[Редукция данных для доминирования в графах]] | |||
== Литература == | |||
1. Bonsma, P.: Spanning trees with many leaves: new extremal results and an improved FPT algorithm. Memorandum Department of Applied Mathematics, vol. 1793, University of Twente,Enschede (2006) | |||
2. Bonsma, P., Brueggemann, T., Woeginger, G.: A faster FPT algorithm for finding spanning trees with many leaves. Proceedings of MFCS 2003. Lecture Notes in Computer Science, vol. 2747, pp. 259-268. Springer, Berlin (2003) | |||
3. Downey, R.G., Fellows, M.R.: Parameterized complexity. Monographs in Computer Science. Springer, New York (1999) | |||
4. Dehne, F., Fellows, M., Langston, M., Rosamond, F., Stevens, K.: An O(2O(k)n3) FPT algorithm for the undirected feedback vertex set problem. Proceedings COCOON 2005. Lecture Notes in Computer Science, vol. 3595, pp. 859-869. Springer, Berlin (2005) | |||
5. Diaz-Gutierrez, P., Bhushan, A., Gopi, M., Pajarola, R.: Single-strips for fast interactive rendering. J. Vis. Comput. 22(6), 372-386 (2006) | |||
6. Dutta, R., Savage, C.: A Note on the Complexity of Converter Placement Supporting Broadcast in WDM Optical Networks. In: Proceedings of the International Conference on Telecommunication Systems-Modeling and Analysis, Dallas, November 2005 ISBN: 0-9716253-3-6 pp. 23-31. American Telecommunication Systems Management Association, Nashville | |||
7. Egecioglu, O., Gonzalez, T.: Minimum-energy Broadcast in Simple Graphs with Limited Node Power. In: Proc. IASTED International Conference on Parallel and Distributed Computing and Systems (PDCS 2001), Anaheim, August 2001 pp. 334-338 | |||
8. Estivill-Castro, V., Fellows, M.R., Langston, M.A., Rosamond, F.A.: FPT is P-time extremal structure I. In: Algorithms and complexity in Durham 2005.Texts in Algorithmics, vol.4, pp. 1-41. Kings College Publications, London (2005) | |||
9. Fellows, M., Langston, M.: On well-partial-order theory and its applications to combinatorial problems of VLSI design. SIAM J. Discret. Math. 5,117-126 (1992) | |||
10. Fellows, M.: Blow-ups, win/win's and crown rules: some new directions in FPT. In: Proceedings of the 29th Workshop on Graph Theoretic Concepts in Computer Science (WG 2003). Lecture Notes in Computer Science, vol. 2880, pp. 1-12. Springer, Berlin (2003) | |||
11. Fellows, M., McCartin, C., Rosamond, F., Stege, U.: Coordinatized kernels and catalytic reductions: an improved FPT algorithm for max leaf spanning tree and other problems. In: Proceedings of the 20th Conference on Foundations of Software Technology and Theoretical Computer Science (FST-TCS 2000). Lecture Notes in Theoretical Computer Science 1974, pp. 240-251. Springer, Berlin (2000) | |||
12. Kleitman, D.J., West, D.B.: Spanning trees with many leaves. SIAM J. Discret. Math. 4,99-106 (1991) | |||
13. Kouider, M., Vestergaard, P.D.: Generalized connected domination in graphs. Discret. Math. Theor. Comput. Sci. (DMTCS) 8, 57-64 (2006) | |||
14. Lu, H.-I., Ravi, R.: Approximating maximum leaf spanning trees in almost linear time. J. Algorithm 29,132-141 (1998) | |||
15. Niedermeier, R.: Invitation to Fixed Parameter Algorithms. Lecture Series in Mathematics and Its Applications, Oxford University Press, Oxford (2006) | |||
16. Prieto-Rodriguez, E.: Systematic kernelization in FPT algorithm design. Dissertation, School of Electrical Engineering and Computer Science, University of Newcastle, Australia (2005) | |||
17. Solis-Oba, R.: 2-approximation algorithm for finding a spanning tree with the maximum number of leaves. In: Proceedings of the 6th Annual European Symposium on Algorithms (ESA'98). Lecture Notes in Computer Science, vol. 1461, pp. 441-452. Springer, Berlin (1998) | |||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 04:55, 22 ноября 2024
Ключевые слова и синонимы
Связное доминирующее множество; экстремальная структура
Постановка задачи
Задача построения остовного дерева с максимальным количеством листьев (ОДМЛ; MAX LEAF SPANNING TREE) заключается в нахождении остовного дерева, имеющего не менее k листьев, в неориентированном графе. Версия разрешимости для параметризованной задачи построения ОДМЛ выглядит следующим образом:
Дано: связный граф G, целое число k.
Параметр: целое число k.
Вопрос: имеет ли граф G остовное дерево с не менее чем k листьями?
Параметризованная сложность недетерминированного полного алгоритма ОДМЛ с полиномиальным временем выполнения широко изучалась [2, 3, 9, 11] с использованием кернелизации, ветвления и других техник с фиксированными параметрами (fixed-parameter tractable, FPT). Авторы работы [8] первыми предложили метод на базе экстремальной структуры для решения сложных вычислительных задач. Этот метод, выполненный в духе Гротендика и следующий в русле проекта миноров графов Робертсона и Сеймура, заключается в том, что математический проект развивается как серия небольших шагов, выполняемых по общей траектории, описываемой подходящей «математической машиной». Авторы подхода предпочитают высказывания следующего типа: каждый связный граф с n вершинами, удовлетворяющий определенному набору свойств, имеет остовное дерево с не менее чем k листьями, и это остовное дерево можно найти за время [math]\displaystyle{ O(f(k) + n^c) \; }[/math], где c – константа (независимая от k), а f - произвольная функция.
При рассмотрении параметризованной сложности значение k называется параметром, который отражает некоторую структуру входных данных или другой аспект цели вычисления. Например, k может обозначать количество ребер, которые необходимо удалить для получения графа без циклов; количество последовательностей ДНК, подлежащих выравниванию в задаче выравнивания последовательностей; максимальную глубину вложенности объявления типа у компилятора; [math]\displaystyle{ k = 1 / \epsilon \; }[/math] может обозначать параметризацию при анализе аппроксимации; кроме того, k также может быть составным значением, зависящим от нескольких переменных.
Существуют два основных способа сравнения FPT-алгоритмов, в результате чего появилось два класса FPT-задач. В классе «f(k)» задача заключается в поиске еще более медленно растущих функций от параметра f(k), управляющих сложностью FPT-алгоритмов. Класс «кернелизации» опирается на следующую лемму, утверждающую, что задача принадлежит к разряду FPT-задач в том и только том случае, если входные данные могут быть предварительно обработаны (кернелизованы) за «обычное» полиномиальное время с получением экземпляра, размер которого ограничивается только функцией от k.
Лемма 1. Параметризованная задача [math]\displaystyle{ \Pi \; }[/math] является задачей с фиксированными параметрами (FPT) в том и только том случае, если существует преобразование с полиномиальным временем выполнения (относительно n и k), переводящее (x, k) в (x', k'), такое, что:
(1) (x, k) является «да-экземпляром» [math]\displaystyle{ \Pi \; }[/math] в том и только том случае, если (x', k') является «да-экземпляром» [math]\displaystyle{ \Pi \; }[/math],
(2) [math]\displaystyle{ k' \le k \; }[/math],
(3) [math]\displaystyle{ |x'| \le g(k) \; }[/math] для некоторой фиксированной функции g.
В ситуации, описываемой леммой, предположим, что мы можем кернелизовать исходные экземпляры до экземпляров размером не более g(k). Два этих класса задач нередко бывают тесно связаны, однако результаты их выполнения различаются. Наилучший известный FPT-алгоритм задачи построения остовного дерева с максимальным количеством листьев с временем выполнения [math]\displaystyle{ O^* (8,12^k) \; }[/math] предложил Бонсма [1] на основе подхода на базе экстремальных структур, который разработали Эстивилл-Кастро, Феллоуз, Лэнгстон и Розамонд [8]. Этот алгоритм определяет, имеет ли граф G с n вершинами остовное дерево не менее чем с k листьями. В то же время авторы работы [8] представили FPT-алгоритм с наименьшим размером ядра.
Можно выделить пять независимых объектов, связанных с теорией экстремальных структур и иллюстрирующих все цели алгоритма построения остовного дерева с максимальным количеством листьев. Перечислим эти пять целей:
(а) Более эффективные FPT-алгоритмы, полученные в результате применения более глубокой теории структур, более мощных правил редукции, связанных с этой теорией, и более сильных доказательств по индукции для улучшенных границ кернелизации.
(б) Правила мощной предварительной обработки (редукции данных / кернелизации) и комбинации правил, которые могут использоваться независимо от того, насколько мал параметр, и могут комбинироваться с другими подходами – например, аппроксимацией и эвристиками. Обычно они несложны для программирования.
(в) Градиенты и правила преобразования для эвристик локального поиска.
(г) Аппроксимационные алгоритмы с полиномиальным временем выполнения и границы эффективности, доказанные систематическим образом.
(д) Структура, используемая для решения других задач.
Основные результаты
Основным результатом является метод экстремальной структуры, используемый в качестве системного подхода к разработке FPT-алгоритмов. Рассмотрим пять перечисленных выше взаимосвязанных целей, проиллюстрировав каждую при помощи данной задачи.
Цель (а): FPT-алгоритмы
Цель заключается в нахождении правил предварительной обработки (кернелизации) с полиномиальным временем выполнения, где g(k) насколько возможно мало. Это будет важно впоследствии в контексте цели (б).
Рис. 1. Правила редукции были выведены для редукции данной структуры графа Клейтмана-Веста
Если перефразировать задачу в терминах теории структур, важнейший вопрос будет звучать следующим образом: какова структура графов, не имеющих подграфа с k листьями? Результат Клейтмана и Веста из теории графов показывает, что граф с минимальной степенью не менее 3, не включающий подграф с k листьями, имеет не более 4(k - 3) вершин. На рис. 1 показано, что это лучший возможный результат для данной гипотезы. Однако исследование структуры при помощи экстремальных методов выявляет необходимость в применении правила редукции, показанного на рис. 2. Примерно двадцати различных правил редукции с полиномиальным временем выполнения (некоторые из них являются намного более сложными и «глобальными» по своей структуре, чем приведенное для примера простое локальное правило редукции) будет достаточно для кернелизации графа с минимальной степенью 2, имеющего не более 3,5k вершин.
Рис. 2. Правило редукции для графа Клейтмана-Веста
В общем случае экземпляр параметризованной задачи состоит из пары (x, k) и «границы», которая вычисляется посредством фиксации x и изменения k с последующим определением, какой ответ имеет задача разрешимости – «да» или «нет». Представляет интерес величина границы при редукции x. Типичная граничная лемма выглядит следующим образом.
Лемма 2. Пусть (G, k) – экземпляр задачи построения остовного дерева с максимальным количеством листьев после редукции, для которого (G, k) является «да-экземпляром», а (G, k + 1) – «нет-экземпляром». Тогда [math]\displaystyle{ |G| \le ck \; }[/math] (где c – небольшая константа, значение которой будет вычислено в результате исследования).
Доказательство граничной леммы выполняется при помощи минимального контрпримера. Контрпримером будет служить граф, такой, что (1) (G, k) – экземпляр задачи ОДМЛ после редукции; (2) (G, k) является «да-экземпляром»; (3) (G, k + 1) является «нет-экземпляром»; (4) |G| > ck.
Доказательство граничной леммы будет производиться последовательным образом. Изначально неизвестно, при каком значении границы будет достигнут успех, а также точно неизвестно, что подразумевается под редукцией. В ходе попытки доказательства эти аспекты станут ясны. По мере раскрытия аргументов особенности структуры подскажут формулировки новых правил редукции. При доказательстве граничной леммы необходимо будет принимать следующие стратегические решения:
(1) Определение полярности границы и формулировка граничной леммы.
(2) Выбор структуры-свидетеля.
(3) Задание индуктивных приоритетов.
(4) Разработка серии утверждений по поводу структуры, описывающих ситуацию на границе.
(5) Определение правил редукции, выполняющихся за полиномиальное время над релевантными структурными ситуациями на границе.
(6) По мере уточнения структуры на границе – заполнение неизвестных компонентов границы кернелизации.
Общая структура аргумента вычисляется при помощи минимального контрпримера согласно приоритетам, заданным в результате выбора (3), который обычно ссылается на выбор (2). Доказательство развивается посредством серии небольших шагов, состоящих из утверждений по поводу структуры, которые в сумме ведут к получению детальной структурной картины на «границе» и, следовательно, позволяют определить границу размера G, которая и представляет собой заключение леммы. Полное доказательство объединяет серию утверждений по поводу дерева-свидетеля, различных множеств вершин и индуктивных приоритетов и формулирует основное неравенство, на основе которого производится доказательство по индукции, и ядро задачи размера 3,5k.
Цель (б): предварительная обработка с полиномиальным временем выполнения и подпрограммы редукции данных
Ниже приводится пример таблицы, используемой для отслеживания каждого возможного состояния границы для возможного решения. Можно привести примеры, демонстрирующие исключительно успешное каскадное применение правил редукции данных к реальным распределениям данных и описывающие разнообразие математических феноменов, относящихся к правилам редукции. Например, некоторые правила редукции – такие как правило разложения на составляющие Клейтмана-Веста для задачи ОДМЛ (рис. 2) – имеют фиксированный «размер границы» (в данном случае равный 2), тогда как правила редукции типа «корона» не имеют такового.
Цель (в): градиенты и преобразования решений для локального поиска
Здесь производится обобщение обычной формулировки для локального поиска, основанное на степени более сложного градиента в процессе получения более высоких границ кернелизации. Первая идея заключается в проведении локального поиска на основе поддержки «текущей структуры-свидетеля», а не полного решения (остовного дерева). Вторая идея состоит в использовании списка индуктивных приоритетов для определения градиента «лучшего решения» для локального поиска.
Цель (г): аппроксимационные алгоритмы с полиномиальным временем выполнения
Теория использования экстремальных структур с полиномиальным временем выполнения напрямую приводит к получению аппроксимационного алгоритма ОДМЛ с константным множителем и полиномиальным временем выполнения. Вначале выполним редукцию G при помощи правил кернелизации. Правила редукции сохраняют параметры аппроксимации. Возьмем любое дерево T (не обязательно остовное) в графе G. Если выполняются все утверждения касательно структуры, тогда (согласно рассуждениям граничной леммы) дерево T должно иметь не менее n/c листьев для c = 3,75. Таким образом, восстановив T с учетом произведенной редукции, получим c-аппроксимацию.
Если по меньшей мере одно утверждение касательно структуры не выполняется, то дерево T можно улучшить, опираясь на один из индуктивных приоритетов. Заметим, что каждое утверждение доказывается посредством рассуждения, которое можно интерпретировать как подпрограмму улучшения T с полиномиальным временем выполнения в случае противоречия утверждению.
Последовательность этих действий можно применить к исходному дереву T (и его потомкам) только полиномиальное количество раз, определяемое списком индуктивных приоритетов, до того момента, как мы получим дерево T', для которого выполняются все утверждения касательно структуры. В этот момент мы должны получить решение с c-аппроксимацией.
Цель (д): структура, используемая для определения экологии сложности
Цель заключается в том, чтобы понять, как именно каждый параметр, определяющий входные данные задачи, влияет на сложность всех других задач. В качестве примера рассмотрим таблицу 1:
Таблица 1. Экология сложности параметров
Здесь используются следующие сокращения: TW – это древесная ширина дерева (TREEWIDTH), BW – ширина полосы (BANDWIDTH), VC – вершинное покрытие (VERTEX COVER), DS – доминирующее множество (DOMINATING SET), G – род (GENUS), а ML – максимальное количество листьев (MAX LEAF). Обозначение во второй строке и четвертом столбце говорит о том, что существует FPT-алгоритм для решения задачи DOMINATING SET на графе G с шириной полосы не более k. Обозначение в четвертой строке и втором столбце говорит о том, что неизвестно, может ли задача BANDWIDTH быть оптимально решена FPT-алгоритмом, если параметром является граница числа доминирования входного графа.
MAX LEAF применяется к последней строке таблицы. Для графов с максимальным количеством листьев, ограниченным k, максимальный размер независимого множества может быть вычислен за время [math]\displaystyle{ O^* (2,972^k) \; }[/math] на основе редукции до ядра размером не более 7k. Использование результата решения одной задачи в качестве исходных данных для другой задачи оказывается весьма практичным.
Применение
Задача построения остовного дерева с максимальным количеством листьев применяется в расчетах компьютерной графики с целью создания представлений полосы треугольников для быстрого интерактивного рендеринга [5]. Также она находит применение в области перераспределения трафика и проектирования сетей – например, для проектирования оптических сетей и распределения используемых длин волн для снижения стоимости сети – в терминах оконечного оборудования либо электронных переключателей [6]. Задача о минимальной энергии в беспроводных сетях заключается в нахождении радиус-вектора передачи для всех станций таким образом, чтобы полная мощность излучения всей сети была насколько возможно малой. Ограниченная версия этой задачи эквивалентна задаче нахождения остовного дерева с максимальным количеством листьев [7]. Задача поиска остовных деревьев с большим числом листьев эквивалентна задаче поиска небольших связных доминирующих множеств и в связи с этим также носит название задачи о минимальном связном доминирующем множестве [13].
Открытые вопросы
Стратегии ветвления
Хотя экстремальные структуры в определенном смысле представляют собой правильный подход к разработке FPT-алгоритма, этот подход не единственный. В частности, он не дает ответа на вопрос, что делать с ядром. Остается открытым вопрос поиска общих стратегий использования «структурной теории с подходящими параметрами» в стратегиях ветвления при анализе ядер в сложных задачах.
Кернелизуемость Тьюринга
Преобразование с полиномиальным временем выполнения (x, k) к более простому редуцированному экземпляру (x', k') является преобразованием «от многих к одному». Можно обобщить понятие редукции «от многих к одному» до редукции Тьюринга. Как должен развиваться поиск экстремальных структур с полиномиальным временем выполнения в контексте такого менее жесткого FPT-алгоритма?
Алгоритмические формы подхода на базе граничной леммы
Из гипотезы граничной леммы о том, что (G, k) является «да-экземпляром», следует, что существует структура, являющаяся свидетелем для данного факта. Не делается предположений о том, что к этой структуре имеется алгоритмический доступ, а когда будут найдены правила редукции, они должны представлять собой преобразования, которые могут быть применены к (G, k) и структуре, которая может быть найдена в (G, k) за полиномиальное время. Иными словами, правила редукции не могут быть определены относительно структуры-свидетеля. Возможно ли описать более общие подходы к кернелизации, при которых структура-свидетель, используемая в ходе доказательства граничной леммы, может быть вычислена за полиномиальное время, и эта структура предоставит условный контекст для некоторых правил редукции? Как эти подходы изменят метод использования экстремальной структуры?
Задача с аннотациями
Можно рассмотреть обобщенную задачу построения остовного дерева с максимальным количеством листьев (MAX LEAF), в которой вершины и ребра имеют различные аннотации, говорящие о том, какие вершины должны быть листьями (или внутренними вершинами) в решении, и т.д. В общем случае подобная обобщенная форма задачи будет сложнее вышеописанной более простой формы. Однако некоторые из «наиболее известных» FPT-алгоритмов для решения различных задач основаны на таких обобщенных формах с аннотациями. В качестве примеров можно привести алгоритмы нахождения доминирующего множества для планарного графа (PLANAR DOMINATING SET) и разрывающего множества вершин (FEEDBACK VERTEX SET) [4]. Должны ли аннотации быть непременным компонентом рецепта наилучшего возможного алгоритма кернелизации с полиномиальным временем выполнения?
См. также
Литература
1. Bonsma, P.: Spanning trees with many leaves: new extremal results and an improved FPT algorithm. Memorandum Department of Applied Mathematics, vol. 1793, University of Twente,Enschede (2006)
2. Bonsma, P., Brueggemann, T., Woeginger, G.: A faster FPT algorithm for finding spanning trees with many leaves. Proceedings of MFCS 2003. Lecture Notes in Computer Science, vol. 2747, pp. 259-268. Springer, Berlin (2003)
3. Downey, R.G., Fellows, M.R.: Parameterized complexity. Monographs in Computer Science. Springer, New York (1999)
4. Dehne, F., Fellows, M., Langston, M., Rosamond, F., Stevens, K.: An O(2O(k)n3) FPT algorithm for the undirected feedback vertex set problem. Proceedings COCOON 2005. Lecture Notes in Computer Science, vol. 3595, pp. 859-869. Springer, Berlin (2005)
5. Diaz-Gutierrez, P., Bhushan, A., Gopi, M., Pajarola, R.: Single-strips for fast interactive rendering. J. Vis. Comput. 22(6), 372-386 (2006)
6. Dutta, R., Savage, C.: A Note on the Complexity of Converter Placement Supporting Broadcast in WDM Optical Networks. In: Proceedings of the International Conference on Telecommunication Systems-Modeling and Analysis, Dallas, November 2005 ISBN: 0-9716253-3-6 pp. 23-31. American Telecommunication Systems Management Association, Nashville
7. Egecioglu, O., Gonzalez, T.: Minimum-energy Broadcast in Simple Graphs with Limited Node Power. In: Proc. IASTED International Conference on Parallel and Distributed Computing and Systems (PDCS 2001), Anaheim, August 2001 pp. 334-338
8. Estivill-Castro, V., Fellows, M.R., Langston, M.A., Rosamond, F.A.: FPT is P-time extremal structure I. In: Algorithms and complexity in Durham 2005.Texts in Algorithmics, vol.4, pp. 1-41. Kings College Publications, London (2005)
9. Fellows, M., Langston, M.: On well-partial-order theory and its applications to combinatorial problems of VLSI design. SIAM J. Discret. Math. 5,117-126 (1992)
10. Fellows, M.: Blow-ups, win/win's and crown rules: some new directions in FPT. In: Proceedings of the 29th Workshop on Graph Theoretic Concepts in Computer Science (WG 2003). Lecture Notes in Computer Science, vol. 2880, pp. 1-12. Springer, Berlin (2003)
11. Fellows, M., McCartin, C., Rosamond, F., Stege, U.: Coordinatized kernels and catalytic reductions: an improved FPT algorithm for max leaf spanning tree and other problems. In: Proceedings of the 20th Conference on Foundations of Software Technology and Theoretical Computer Science (FST-TCS 2000). Lecture Notes in Theoretical Computer Science 1974, pp. 240-251. Springer, Berlin (2000)
12. Kleitman, D.J., West, D.B.: Spanning trees with many leaves. SIAM J. Discret. Math. 4,99-106 (1991)
13. Kouider, M., Vestergaard, P.D.: Generalized connected domination in graphs. Discret. Math. Theor. Comput. Sci. (DMTCS) 8, 57-64 (2006)
14. Lu, H.-I., Ravi, R.: Approximating maximum leaf spanning trees in almost linear time. J. Algorithm 29,132-141 (1998)
15. Niedermeier, R.: Invitation to Fixed Parameter Algorithms. Lecture Series in Mathematics and Its Applications, Oxford University Press, Oxford (2006)
16. Prieto-Rodriguez, E.: Systematic kernelization in FPT algorithm design. Dissertation, School of Electrical Engineering and Computer Science, University of Newcastle, Australia (2005)
17. Solis-Oba, R.: 2-approximation algorithm for finding a spanning tree with the maximum number of leaves. In: Proceedings of the 6th Annual European Symposium on Algorithms (ESA'98). Lecture Notes in Computer Science, vol. 1461, pp. 441-452. Springer, Berlin (1998)