Деревья Штейнера: различия между версиями
Irina (обсуждение | вклад) м (→См. также) |
KVN (обсуждение | вклад) |
||
| (не показано 38 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
== Ключевые слова и синонимы == | == Ключевые слова и синонимы == | ||
Разработка алгоритма | Разработка аппроксимационного алгоритма | ||
== Определение == | == Определение == | ||
Пусть дано множество точек, называемых полюсами, в метрическом пространстве. Задача заключается в нахождении кратчайшего дерева, связывающего все точки. В случае деревьев Штейнера используются три основных метрических пространства: евклидова плоскость, плоскость с прямолинейными расстояниями и сеть с взвешенными ребрами. | Пусть дано множество точек, называемых полюсами, в метрическом пространстве. Задача заключается в нахождении кратчайшего дерева, связывающего все точки. В случае деревьев Штейнера используются три основных метрических пространства: евклидова плоскость, плоскость с прямолинейными расстояниями и сеть с взвешенными ребрами. Задачи построения [[дерево Штейнера|дерева Штейнера]] в этих метрических пространствах носят названия [[Евклидова задача Штейнера|евклидовой задачи Штейнера]] (Euclidean Steiner Tree, EST), ''прямолинейного дерева Штейнера'' (Rectilinear Steiner Tree, RST) и ''сетевого дерева Штейнера'' (Network Steiner Tree, NST), соответственно. Было обнаружено, что для EST и RST имеются аппроксимационные схемы с полиномиальным временем выполнения (PTAS) при помощи адаптивного разбиения. Однако для NST существует положительное число r, такое, что вычисление r-аппроксимации является NP-полной задачей. До настоящего момента лучший коэффициент эффективности для аппроксимации NST с полиномиальным временем выполнения был получен при помощи k-ограниченных деревьев Штейнера. Однако на практике очень часто используется итеративное 1-дерево Штейнера. Фактически итеративное 1-дерево Штейнера уже давно предлагалось в качестве кандидата на хорошую аппроксимацию минимальных деревьев Штейнера. Оно отлично проявило себя в компьютерных экспериментах, однако не было проведено корректного анализа, который показал бы, что коэффициент эффективности итеративного 1-дерева Штейнера превосходит коэффициент эффективности минимального остовного дерева. Недавно такую работу проделали Ду и коллеги [9]. Небольшое различие в построении 3-ограниченного дерева Штейнера и итеративного 1-дерева Штейнера приводит к значительному различию при анализе этих двух типов деревьев. В чем заключается сложность такого анализа? Это будет описано ниже. | ||
== История и предпосылки == | == История и предпосылки == | ||
Задача построения дерева Штейнера была предложена Гауссом в 1835 году в виде обобщения задачи Ферма. Пусть даны три точки A, B и C на евклидовой плоскости. Ферма изучал задачу нахождения точки S, для которой |SA| + |SB| + |SC| будет минимально. Он обнаружил, что в случае, когда все три внутренних угла треугольника ABC имеют величину менее 120°, оптимальная точка S должна | Задача построения дерева Штейнера была предложена Карлом Фридрихом Гауссом в 1835 году в виде обобщения задачи Ферма. Пусть даны три точки A, B и C на евклидовой плоскости. Ферма изучал задачу нахождения точки S, для которой |SA| + |SB| + |SC| будет минимально. Он обнаружил, что в случае, когда все три внутренних угла треугольника ABC имеют величину менее 120°, оптимальная точка S должна находиться в положении <math>\angle ASB = \angle BSC = \angle CSA = 120^{\circ} \;</math>. | ||
| Строка 21: | Строка 20: | ||
[[Файл:Steiner_trees_01.png]] | |||
Рисунок 1. | |||
21 марта 1836 в ответном письме Гаусс | 21 марта 1836 в ответном письме Гаусс пояснил Шумахеру, что ошибка в парадоксе Ферма возникает в тот момент, когда задача Ферма для четырех точек A, B, C, D заменяется на задачу для трех точек F, C, D. Когда A и B оказываются идентичными F, суммарное расстояние от E до четырех точек A, B, C и D равняется 2|EF| + |EC| + |ED|, а не |EF| + |EC| + |ED|. Следовательно, точка E не может быть решением задачи Ферма для F, C и D. Что более важно, Гаусс предложил новую задачу. По его мнению, интереснее было бы найти кратчайшую сеть, а не точку. Гаусс также предложил несколько возможных вариантов соединений кратчайшей сети для четырех заданных точек. | ||
К сожалению, исследователи деревьев Штейнера на ранней стадии изучения вопроса не были знакомы с письмом Гаусса. Рихард Курант и Герберт Роббинс в своей популярной книге «Что такое математика?» , опубликованной в 1941 году, назвали задачу Гаусса деревом Штейнера, так что именно это наименование получило широкое распространение. | К сожалению, исследователи деревьев Штейнера на ранней стадии изучения вопроса не были знакомы с письмом Гаусса. Рихард Курант и Герберт Роббинс в своей популярной книге «Что такое математика?» [6], опубликованной в 1941 году, назвали задачу Гаусса деревом Штейнера, так что именно это наименование получило широкое распространение. | ||
| Строка 33: | Строка 34: | ||
Хорошо известной задачей является гипотеза Гилберта-Поллака об отношении Штейнера, представляющем собой минимальное отношение длин между минимальным деревом Штейнера и минимальным остовным деревом | Хорошо известной задачей является гипотеза Гилберта-Поллака об отношении Штейнера, представляющем собой минимальное отношение длин между минимальным деревом Штейнера и минимальным остовным деревом на том же множестве точек. Гилберт и Поллак в 1968 году предположили, что отношение Штейнера на евклидовой плоскости равно <math>\sqrt{3} / 2 \;</math> и достигается для трех вершин равностороннего треугольника. Доказательству этой гипотезы было посвящено множество работ, в конечном итоге ее доказали Ду и Хван [7]. | ||
Еще одной важной задачей является задача [[лучшая аппроксимация|лучшей аппроксимации]]. Довольно долгое время не удавалось доказать наличие аппроксимации с коэффициентом эффективности меньше обратного значения отношения Штейнера. Первый прорыв совершил Зеликовский [14], который нашел 11/6-аппроксимацию с полиномиальным временем выполнения для задачи NST, что лучше 1/2 – обратного значения отношения Штейнера для сети с взвешенными ребрами [''прим. переводчика: вероятно, имелось в виду значение 2, а не 1/2?'']. Позднее Берман и Рамайе [2] предложили 92/72-аппроксимацию с полиномиальным временем выполнения для RST, а Ду, Цзян и Фэн [8] закрыли тему, показав, что в любом метрическом пространстве существует аппроксимация с полиномиальным временем выполнения с коэффициентом эффективности меньше обратного значения отношения Штейнера, при условии, что для любого множества с фиксированным количеством точек его минимальное дерево Штейнера вычислимо за полиномиальное время. | |||
Все вышеперечисленные аппроксимации были созданы на базе семейства k-ограниченных деревьев Штейнера. В результате улучшения некоторых деталей построения константный коэффициент эффективности удалось понизить, однако при этом улучшения также становятся меньше. В 1996 году Ароре [1] удалось достичь значительного прогресса в решении задач EST и RST. Он доказал существование PTAS для этих двух задач. Таким образом, исследователи-теоретики теперь основное внимание уделяют задаче NST. Берн и Плассман [3] показали, что эта задача является MaxSNP-полной. Это означает, что существует положительное число r, такое, что вычисление r-аппроксимации для NST является NP-полной задачей. Самый эффективный на данный момент алгоритм построения NST предложили Робин и Зеликовский [12]. Они также дали очень простой анализ хорошо известной эвристики – итеративного 1-дерева Штейнера для псевдодвудольных графов. | |||
Анализ итеративного 1-дерева Штейнера также долго время оставался нерешенной задачей. С тех пор как Чанг [4, 5] в 1972 году предположил, что итеративное 1-дерево Штейнера аппроксимирует минимальное дерево Штейнера, его эффективность в компьютерных экспериментах оказалась весьма высокой [10, 13], однако подкреплений со стороны теоретического анализа этому утверждению до сих пор не найдено. Фактически и k-ограниченное дерево Штейнера, и итеративное 1-дерево Штейнера строятся при помощи жадных алгоритмов, но с различными типами гармонических функций. В случае итеративного 1-дерева Штейнера гармоническая функция не является субмодулярной, тогда как в случае k-ограниченного дерева Штейнера она является таковой; свойство, выполняющееся для второго типа деревьев, может оказаться неверным для первого. Оказалось, что субмодулярность гармонической функции исключительно важна для анализа жадных аппроксимаций [11]. Ду и др. [9] дали точный анализ для итеративного 1-дерева Штейнера при помощи обобщенной техники обработки несубмодулярной гармонической функции. | |||
== Основные результаты == | |||
Рассмотрим входной граф с взвешенными ребрами G = (V, E) для задачи построения NST (сетевого дерева Штейнера). Предположим, что G – полный граф и что веса ребер удовлетворяют неравенству треугольника. В противном случае рассмотрим полный граф на V, в котором каждое ребро (u, v) имеет вес, равный длине кратчайшего пути между u и v в графе G. Пусть дано множество полюсов P; [[дерево Штейнера|деревом Штейнера]] является дерево, связывающее все указанные полюса таким образом, что каждый лист является полюсом. | |||
В дереве Штейнера полюс может иметь степень больше единицы. Можно провести декомпозицию дерева Штейнера, разбив все вершины со степенью больше 1 на меньшие деревья, в которых каждый полюс является листом. В такой декомпозиции каждое полученное маленькое дерево называется [[полный компонент|полным компонентом]]. Размер полного компонента равен количеству содержащихся в нем полюсов. Дерево Штейнера является k-ограниченным, если каждый его полный компонент имеет размер не более k. Кратчайшее k-ограниченное дерево Штейнера также называется k-ограниченным [[минимальное дерево Штейнера|минимальным деревом Штейнера]]. Обозначим его длину за <math>smt_k(P) \;</math>. Очевидно, что <math>smt_2(P) \;</math> – длина минимального остовного дерева на P, также обозначаемая как mst(P). Пусть smt(P) обозначает длину минимального дерева Штейнера на P. Если значение <math>smt_3(P) \;</math> можно вычислить за полиномиальное время, то этот способ лучше подходит для аппроксимации smt(P) по сравнению с mst(P). Однако до сих пор для <math>smt_3(P) \;</math> не было найдено аппроксимации с полиномиальным временем. Поэтому Зеликовский [14] использовал жадную аппроксимацию <math>smt_3(P) \;</math> для аппроксимации smt(P). Чанг [4, 5] использовал похожий жадный алгоритм для вычисления итеративного 1-дерева Штейнера. Пусть <math>\mathcal{F} \;</math> – семейство подграфов исходного графа G с взвешенными ребрами. Для любого связного подграфа H обозначим за mst(H) длину минимального остовного дерева H, а за mst(H) – сумму mst(H') для H' по всем связным компонентам для любого подграфа H. | |||
Определим gain(H) = mst(P) - mst(P : H) - mst(H), где mst(P : H) – длина минимального остовного дерева, связывающего все несвязанные полюса в P после того, как каждое ребро H будет стянуто в точку. | |||
'''Жадный алгоритм <math>H \gets \empty \;</math>;''' | |||
'''while''' в P остаются не связанные с H элементы '''do''' | |||
выбрать <math>F \in \mathcal{F} \;</math> так, чтобы максимизировать gain(H <math>\cup \;</math> F); | |||
выдать результат mst(H). | |||
Если множество <math>\mathcal{F} \;</math> состоит из всех полных компонентов размером не более 3, этот жадный алгоритм дает на выходе 3-ограниченное дерево Штейнера, введенное Зеликовским [14]. Если <math>\mathcal{F} \;</math> состоит из всех трехлучевых звезд и всех ребер (где трехлучевая звезда представляет собой дерево с 3 листьями и центральной вершиной), то этот жадный алгоритм дает на выходе итеративное 1-дерево Штейнера. Интересный факт, на которой обратили внимание Ду и коллеги [9], заключается в том, что функция gain(<math>\cdot</math>) является субмодулярной над всеми полными компонентами размера не более 3, но не является субмодулярной над всеми трехлучевыми звездами и ребрами. | |||
Рассмотрим базовое множество E и функцию f, областью определения которой являются все подмножества E, а областью значений – вещественные числа. f является [[субмодулярная функция|субмодулярной]], если для любых двух подмножеств A, B множества E выполняется соотношение | |||
<math>f(A) + f(B) \ge f(A \cup B) + f(A \cap B) \;</math> | |||
Для <math>x \in E \;</math> и <math>A \subseteq E \;</math> обозначим <math>\Delta_x f(A) = f(A \cup \{ x \}) - f(A) \;</math>. | |||
'''Лемма 1.''' Функция f является субмодулярной в том и только том случае, если для любых <math>A \subset E \;</math> и различных <math>x, y \in E - A \;</math> выполняется соотношение | |||
(1) <math>\Delta_x \; \Delta_y \; f(A) \le 0</math> | |||
Доказательство. Предположим, что f является субмодулярной. Положим <math>B = A \cup \{ x \} \;</math> и <math>C = A \cup \{ y \} \;</math>. Тогда <math>B \cup C = A \cup A \cup \{ x, y \} \;</math> и <math>B \cap C = A \;</math>. Следовательно, имеет место | |||
<math>f(A \cup \{ x, y \}) - f(A \cup \{ x \}) - f(A \cup \{ y \}) + f(A) \le 0 \;</math>, | |||
( | |||
это означает, что соотношение (1) верно. | это означает, что соотношение (1) верно. | ||
Напротив, предположим, что свойство (1) выполняется для любых A | Напротив, предположим, что свойство (1) выполняется для любых <math>A \subset E \;</math> и различных <math>x, y \in E - A \;</math>. Рассмотрим два подмножества A, B множества E. Если <math>A \subseteq B \;</math> или <math>B \subseteq A \;</math>, тогда тривиально получается | ||
f(A) + f(B) | |||
<math>f(A) + f(B) \ge f(A \cup B) + f(A \cap B) \;</math>. | |||
Следовательно, должно иметь место A | Следовательно, должно иметь место <math>A \backslash B \ne \empty \;</math> и <math>B \backslash A \ne \empty \;</math>. Запишем это как <math>A \backslash B = \{ x_1, ..., x_k \} \;</math> и <math>B \backslash A = \{ y_1, ..., y_h \} \;</math>. Тогда | ||
<math>f(A \; \cup \; B) - f(A) - f(B) + f(A \; \cap \; B) = \sum^k_{i = 1} \sum^h_{j = 1} \Delta_{x_i} \Delta_{y_j} f(A \; \cup \; \{ x_1, ..., x_{i - 1} \} \; \cup \; \{ y_1, ..., y_{j - 1} \}) \le 0</math>, | |||
f( | где <math>\{ x_1, ..., x_{i - 1} \} = \empty \;</math> для i = 1 и <math>\{ y_1, ..., y_{j - 1} \} = \empty \;</math> для j = 1. | ||
< | |||
где | |||
Лемма 2. Определим f(H) = | '''Лемма 2.''' Определим f(H) = -mst(P : H). Тогда функция f является субмодулярной над множеством ребер E. | ||
Доказательство. Заметим, что для любых двух различных ребер x и y, не принадлежащих подграфу H, | Доказательство. Заметим, что для любых двух различных ребер x и y, не принадлежащих подграфу H, | ||
<math>\Delta_x \Delta_y f(H) = -mst(P : H \; \cup \; x \; \cup \; y) + mst(P : H \; \cup \; x) + mst(P : H \; \cup \; y) - mst(P : H) = (mst(P : H) - mst(P : H \; \cup x \; \cup \; y)) - (mst(P : H) - mst(P : H \; \cup \; x)) + (mst(P : H) - mst(P : H \; \cup \; y))</math>. | |||
Пусть T – минимальное остовное дерево для несвязанных полюсов после стягивания каждого ребра H в точку. T содержит путь <math>P_x \;</math>, соединяющий две конечные точки x, и путь <math>P_y \;</math>, соединяющий две конечные точки y. Пусть <math>e_x (e_y) \;</math> – самое длинное ребро пути <math>P_x (P_y) \;</math>. Тогда | |||
<math>mst(P : H) - mst(P : H \; \cup \; x) = length(e_x)</math>; | |||
<math>mst(P : H) - mst(P : H \; \cup \; y) = length(e_y)</math>. | |||
Значение <math>mst(P : H) - mst(P : H \; \cup \; x \; \cup \; y)</math> можно вычислить следующим образом: выберем самое длинное ребро e' из <math>P_x \cup P_y</math>. Заметим, что <math>T \cup x \cup y - e'</math> содержит уникальный цикл Q. Выберем самое длинное ребро e" из <math>(P_x \cup P_y) \cap Q</math>. Тогда | |||
<math>mst(P : H) - mst(P : H \cup x \cup y) = length(e') + length(e'')</math>. | |||
Теперь, чтобы показать субмодулярность f, достаточно доказать неравенство | |||
(2) <math>length(e_x) + length(e_y) \ge length(e') + length(e'')</math>. | |||
Случай | Случай 1. <math>e_x \notin P_x \cap P_y</math> и <math>e_y \notin P_x \cap P_y</math>. Без потери общности будем считать, что <math>length(e_x) \ge length(e_y) \;</math>. Тогда можно выбрать <math>e' = e_x \;</math> таким образом, что <math>(P_x \cup P_y) \cap Q = P_y</math>. Следовательно, можно выбрать <math>e'' = e_y \;</math>. Таким образом, выполняется равенство для (2). | ||
Случай | Случай 2. <math>e_x \notin P_x \cap P_y</math> и <math>e_y \in P_x \cap P_y</math>. Очевидно, что <math>length(e_x) \ge length(e_y)</math>. Тогда можно выбрать <math>e' = e_x \;</math> таким образом, что <math>(P_x \cup P_y) \cap Q = P_y</math>. Следовательно, можно выбрать <math>e'' = e_y \;</math>. Таким образом, выполняется равенство для (2). | ||
Случай 3. <math>e_x \in P_x \cap P_y</math> и <math>e_y \notin P_x \cap P_y</math>. Аналогично случаю 2. | |||
Случай 4. <math>e_x \in P_x \cap P_y</math> и <math>e_y \in P_x \cap P_y</math>. В этом случае <math>length(e_x) = length(e_y) = length(e') \;</math>. Таким образом, (2) верно. □ | |||
Далее поясняется, что субмодулярность gain(<math>\cdot</math>) имеет место для k-ограниченного дерева Штейнера. | |||
'''Предположение'''. Пусть <math>\mathcal{E} \;</math> – множество всех полных компонентов дерева Штейнера. Тогда gain(<math>\cdot</math>) как функция от множества всех подмножеств <math>\mathcal{E} \;</math> является субмодулярной. | |||
Доказательство. Заметим, что для любых <math>\mathcal{H} \subset \mathcal{E} \;</math> и <math>x, y \in \mathcal{E} - \mathcal{H} \;</math> верно <math>\Delta_x \Delta_y mst(H) = 0 \;</math>, где <math>H = \cup_{z \in \mathcal{H}} z \;</math>. Таким образом, верность предположения следует из леммы 2. □ | |||
Пусть <math>\mathcal{F} \;</math> – множество трехлучевых звезд и ребер, выбранных жадным алгоритмом для вычисления итеративного 1-дерева Штейнера. Тогда gain(<math>\cdot</math>) может и не быть субмодулярной на <math>\mathcal{F} \;</math>. Чтобы убедиться в этом, рассмотрим две трехлучевых звезды x и y на рис. 2. Заметим, что <math>gain(x \cup y) > gain(x), gain(y) \le 0, gain(\empty) = 0 \;</math>. Имеет место соотношение | |||
<math>gain(x \cup y) - gain(x) - gain(y) + gain(\empty) > 0 \;</math>. | |||
[[Файл:Steiner_trees_02.png]] | |||
Рисунок 2. | |||
== Применение == | == Применение == | ||
Задача построения дерева Штейнера является классической NP-полной проблемой и имеет множество приложений | Задача построения дерева Штейнера является классической NP-полной проблемой и имеет множество приложений при разработке компьютерных микросхем, междугородних телефонных линий, многоадресной маршрутизации в сетях телекоммуникаций и т.п. Разработано множество эвристик жадного типа для построения деревьев Штейнера. Большинство из них демонстрируют высокую эффективность в компьютерных экспериментах, однако без подкрепления со стороны теоретического анализа. Предложенный подход может стать его основой. | ||
== Открытые вопросы == | == Открытые вопросы == | ||
До сих пор неясно, является ли задача построения 3-ограниченного минимального дерева Штейнера NP-полной. Известно, что она является таковой при построении k-ограниченного минимального дерева Штейнера при k > | До сих пор неясно, является ли задача построения 3-ограниченного минимального дерева Штейнера NP-полной. Известно, что она является таковой при построении k-ограниченного минимального дерева Штейнера при <math>k \ge 4 \;</math>. | ||
| Строка 146: | Строка 164: | ||
* ''[[Минимальные остовные деревья]] | * ''[[Минимальные остовные деревья]] | ||
* ''[[Прямолинейное дерево Штейнера]] | * ''[[Прямолинейное дерево Штейнера]] | ||
== Литература == | == Литература == | ||
| Строка 175: | Строка 194: | ||
14. Zelikovsky, A.Z.: The 11/6-approximation algorithm for the Steiner problem on networks. Algorithmica 9,463^70 (1993) | 14. Zelikovsky, A.Z.: The 11/6-approximation algorithm for the Steiner problem on networks. Algorithmica 9,463^70 (1993) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 04:52, 22 ноября 2024
Ключевые слова и синонимы
Разработка аппроксимационного алгоритма
Определение
Пусть дано множество точек, называемых полюсами, в метрическом пространстве. Задача заключается в нахождении кратчайшего дерева, связывающего все точки. В случае деревьев Штейнера используются три основных метрических пространства: евклидова плоскость, плоскость с прямолинейными расстояниями и сеть с взвешенными ребрами. Задачи построения дерева Штейнера в этих метрических пространствах носят названия евклидовой задачи Штейнера (Euclidean Steiner Tree, EST), прямолинейного дерева Штейнера (Rectilinear Steiner Tree, RST) и сетевого дерева Штейнера (Network Steiner Tree, NST), соответственно. Было обнаружено, что для EST и RST имеются аппроксимационные схемы с полиномиальным временем выполнения (PTAS) при помощи адаптивного разбиения. Однако для NST существует положительное число r, такое, что вычисление r-аппроксимации является NP-полной задачей. До настоящего момента лучший коэффициент эффективности для аппроксимации NST с полиномиальным временем выполнения был получен при помощи k-ограниченных деревьев Штейнера. Однако на практике очень часто используется итеративное 1-дерево Штейнера. Фактически итеративное 1-дерево Штейнера уже давно предлагалось в качестве кандидата на хорошую аппроксимацию минимальных деревьев Штейнера. Оно отлично проявило себя в компьютерных экспериментах, однако не было проведено корректного анализа, который показал бы, что коэффициент эффективности итеративного 1-дерева Штейнера превосходит коэффициент эффективности минимального остовного дерева. Недавно такую работу проделали Ду и коллеги [9]. Небольшое различие в построении 3-ограниченного дерева Штейнера и итеративного 1-дерева Штейнера приводит к значительному различию при анализе этих двух типов деревьев. В чем заключается сложность такого анализа? Это будет описано ниже.
История и предпосылки
Задача построения дерева Штейнера была предложена Карлом Фридрихом Гауссом в 1835 году в виде обобщения задачи Ферма. Пусть даны три точки A, B и C на евклидовой плоскости. Ферма изучал задачу нахождения точки S, для которой |SA| + |SB| + |SC| будет минимально. Он обнаружил, что в случае, когда все три внутренних угла треугольника ABC имеют величину менее 120°, оптимальная точка S должна находиться в положении [math]\displaystyle{ \angle ASB = \angle BSC = \angle CSA = 120^{\circ} \; }[/math].
Обобщение задачи Ферма можно произвести по двум направлениям:
1. Пусть имеется n точек на евклидовой плоскости. Найти точку S с минимальным суммарным расстоянием от S до заданных n точек. Эта задача также называется задачей Ферма.
2. Пусть имеется n точек на евклидовой плоскости. Найти кратчайшую сеть, соединяющую все точки.
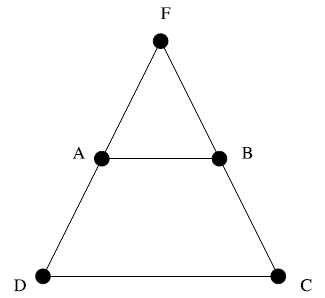
Гаусс решил вторую обобщенную задачу в переписке с Шумахером. 19 марта 1836 Генрих Христиан Шумахер в письме Гауссу упомянул парадокс, связанный с задачей Ферма. Рассмотрим выпуклый четырехугольник ABCD. Известно, что решение задачи Ферма для четырех точек A, B, C, D представляет собой пересечение E диагоналей AC и BD. Предположим, что продолжение отрезков DA и CB дает точку пересечения F. Переместим A и B в F. Тогда E также будет перемещена в F. Однако в случае, если величина угла при F меньше 120°, точка F не может быть решением задачи Ферма для исходных точек F, D и C. В чем же дело? (См. рис. 1).
Рисунок 1.
21 марта 1836 в ответном письме Гаусс пояснил Шумахеру, что ошибка в парадоксе Ферма возникает в тот момент, когда задача Ферма для четырех точек A, B, C, D заменяется на задачу для трех точек F, C, D. Когда A и B оказываются идентичными F, суммарное расстояние от E до четырех точек A, B, C и D равняется 2|EF| + |EC| + |ED|, а не |EF| + |EC| + |ED|. Следовательно, точка E не может быть решением задачи Ферма для F, C и D. Что более важно, Гаусс предложил новую задачу. По его мнению, интереснее было бы найти кратчайшую сеть, а не точку. Гаусс также предложил несколько возможных вариантов соединений кратчайшей сети для четырех заданных точек.
К сожалению, исследователи деревьев Штейнера на ранней стадии изучения вопроса не были знакомы с письмом Гаусса. Рихард Курант и Герберт Роббинс в своей популярной книге «Что такое математика?» [6], опубликованной в 1941 году, назвали задачу Гаусса деревом Штейнера, так что именно это наименование получило широкое распространение.
Дерево Штейнера стало популярной темой исследований в математике и компьютерных науках в связи с его широким применением в области телекоммуникаций и компьютерных сетей. Начиная с опубликованной в 1968 году работы Гилберта и Поллака, было выпущено множество работ, посвященных различным задачам, связанным с деревьями Штейнера.
Хорошо известной задачей является гипотеза Гилберта-Поллака об отношении Штейнера, представляющем собой минимальное отношение длин между минимальным деревом Штейнера и минимальным остовным деревом на том же множестве точек. Гилберт и Поллак в 1968 году предположили, что отношение Штейнера на евклидовой плоскости равно [math]\displaystyle{ \sqrt{3} / 2 \; }[/math] и достигается для трех вершин равностороннего треугольника. Доказательству этой гипотезы было посвящено множество работ, в конечном итоге ее доказали Ду и Хван [7].
Еще одной важной задачей является задача лучшей аппроксимации. Довольно долгое время не удавалось доказать наличие аппроксимации с коэффициентом эффективности меньше обратного значения отношения Штейнера. Первый прорыв совершил Зеликовский [14], который нашел 11/6-аппроксимацию с полиномиальным временем выполнения для задачи NST, что лучше 1/2 – обратного значения отношения Штейнера для сети с взвешенными ребрами [прим. переводчика: вероятно, имелось в виду значение 2, а не 1/2?]. Позднее Берман и Рамайе [2] предложили 92/72-аппроксимацию с полиномиальным временем выполнения для RST, а Ду, Цзян и Фэн [8] закрыли тему, показав, что в любом метрическом пространстве существует аппроксимация с полиномиальным временем выполнения с коэффициентом эффективности меньше обратного значения отношения Штейнера, при условии, что для любого множества с фиксированным количеством точек его минимальное дерево Штейнера вычислимо за полиномиальное время.
Все вышеперечисленные аппроксимации были созданы на базе семейства k-ограниченных деревьев Штейнера. В результате улучшения некоторых деталей построения константный коэффициент эффективности удалось понизить, однако при этом улучшения также становятся меньше. В 1996 году Ароре [1] удалось достичь значительного прогресса в решении задач EST и RST. Он доказал существование PTAS для этих двух задач. Таким образом, исследователи-теоретики теперь основное внимание уделяют задаче NST. Берн и Плассман [3] показали, что эта задача является MaxSNP-полной. Это означает, что существует положительное число r, такое, что вычисление r-аппроксимации для NST является NP-полной задачей. Самый эффективный на данный момент алгоритм построения NST предложили Робин и Зеликовский [12]. Они также дали очень простой анализ хорошо известной эвристики – итеративного 1-дерева Штейнера для псевдодвудольных графов.
Анализ итеративного 1-дерева Штейнера также долго время оставался нерешенной задачей. С тех пор как Чанг [4, 5] в 1972 году предположил, что итеративное 1-дерево Штейнера аппроксимирует минимальное дерево Штейнера, его эффективность в компьютерных экспериментах оказалась весьма высокой [10, 13], однако подкреплений со стороны теоретического анализа этому утверждению до сих пор не найдено. Фактически и k-ограниченное дерево Штейнера, и итеративное 1-дерево Штейнера строятся при помощи жадных алгоритмов, но с различными типами гармонических функций. В случае итеративного 1-дерева Штейнера гармоническая функция не является субмодулярной, тогда как в случае k-ограниченного дерева Штейнера она является таковой; свойство, выполняющееся для второго типа деревьев, может оказаться неверным для первого. Оказалось, что субмодулярность гармонической функции исключительно важна для анализа жадных аппроксимаций [11]. Ду и др. [9] дали точный анализ для итеративного 1-дерева Штейнера при помощи обобщенной техники обработки несубмодулярной гармонической функции.
Основные результаты
Рассмотрим входной граф с взвешенными ребрами G = (V, E) для задачи построения NST (сетевого дерева Штейнера). Предположим, что G – полный граф и что веса ребер удовлетворяют неравенству треугольника. В противном случае рассмотрим полный граф на V, в котором каждое ребро (u, v) имеет вес, равный длине кратчайшего пути между u и v в графе G. Пусть дано множество полюсов P; деревом Штейнера является дерево, связывающее все указанные полюса таким образом, что каждый лист является полюсом.
В дереве Штейнера полюс может иметь степень больше единицы. Можно провести декомпозицию дерева Штейнера, разбив все вершины со степенью больше 1 на меньшие деревья, в которых каждый полюс является листом. В такой декомпозиции каждое полученное маленькое дерево называется полным компонентом. Размер полного компонента равен количеству содержащихся в нем полюсов. Дерево Штейнера является k-ограниченным, если каждый его полный компонент имеет размер не более k. Кратчайшее k-ограниченное дерево Штейнера также называется k-ограниченным минимальным деревом Штейнера. Обозначим его длину за [math]\displaystyle{ smt_k(P) \; }[/math]. Очевидно, что [math]\displaystyle{ smt_2(P) \; }[/math] – длина минимального остовного дерева на P, также обозначаемая как mst(P). Пусть smt(P) обозначает длину минимального дерева Штейнера на P. Если значение [math]\displaystyle{ smt_3(P) \; }[/math] можно вычислить за полиномиальное время, то этот способ лучше подходит для аппроксимации smt(P) по сравнению с mst(P). Однако до сих пор для [math]\displaystyle{ smt_3(P) \; }[/math] не было найдено аппроксимации с полиномиальным временем. Поэтому Зеликовский [14] использовал жадную аппроксимацию [math]\displaystyle{ smt_3(P) \; }[/math] для аппроксимации smt(P). Чанг [4, 5] использовал похожий жадный алгоритм для вычисления итеративного 1-дерева Штейнера. Пусть [math]\displaystyle{ \mathcal{F} \; }[/math] – семейство подграфов исходного графа G с взвешенными ребрами. Для любого связного подграфа H обозначим за mst(H) длину минимального остовного дерева H, а за mst(H) – сумму mst(H') для H' по всем связным компонентам для любого подграфа H.
Определим gain(H) = mst(P) - mst(P : H) - mst(H), где mst(P : H) – длина минимального остовного дерева, связывающего все несвязанные полюса в P после того, как каждое ребро H будет стянуто в точку.
Жадный алгоритм [math]\displaystyle{ H \gets \empty \; }[/math]; while в P остаются не связанные с H элементы do выбрать [math]\displaystyle{ F \in \mathcal{F} \; }[/math] так, чтобы максимизировать gain(H [math]\displaystyle{ \cup \; }[/math] F); выдать результат mst(H).
Если множество [math]\displaystyle{ \mathcal{F} \; }[/math] состоит из всех полных компонентов размером не более 3, этот жадный алгоритм дает на выходе 3-ограниченное дерево Штейнера, введенное Зеликовским [14]. Если [math]\displaystyle{ \mathcal{F} \; }[/math] состоит из всех трехлучевых звезд и всех ребер (где трехлучевая звезда представляет собой дерево с 3 листьями и центральной вершиной), то этот жадный алгоритм дает на выходе итеративное 1-дерево Штейнера. Интересный факт, на которой обратили внимание Ду и коллеги [9], заключается в том, что функция gain([math]\displaystyle{ \cdot }[/math]) является субмодулярной над всеми полными компонентами размера не более 3, но не является субмодулярной над всеми трехлучевыми звездами и ребрами.
Рассмотрим базовое множество E и функцию f, областью определения которой являются все подмножества E, а областью значений – вещественные числа. f является субмодулярной, если для любых двух подмножеств A, B множества E выполняется соотношение
[math]\displaystyle{ f(A) + f(B) \ge f(A \cup B) + f(A \cap B) \; }[/math]
Для [math]\displaystyle{ x \in E \; }[/math] и [math]\displaystyle{ A \subseteq E \; }[/math] обозначим [math]\displaystyle{ \Delta_x f(A) = f(A \cup \{ x \}) - f(A) \; }[/math].
Лемма 1. Функция f является субмодулярной в том и только том случае, если для любых [math]\displaystyle{ A \subset E \; }[/math] и различных [math]\displaystyle{ x, y \in E - A \; }[/math] выполняется соотношение
(1) [math]\displaystyle{ \Delta_x \; \Delta_y \; f(A) \le 0 }[/math]
Доказательство. Предположим, что f является субмодулярной. Положим [math]\displaystyle{ B = A \cup \{ x \} \; }[/math] и [math]\displaystyle{ C = A \cup \{ y \} \; }[/math]. Тогда [math]\displaystyle{ B \cup C = A \cup A \cup \{ x, y \} \; }[/math] и [math]\displaystyle{ B \cap C = A \; }[/math]. Следовательно, имеет место
[math]\displaystyle{ f(A \cup \{ x, y \}) - f(A \cup \{ x \}) - f(A \cup \{ y \}) + f(A) \le 0 \; }[/math],
это означает, что соотношение (1) верно.
Напротив, предположим, что свойство (1) выполняется для любых [math]\displaystyle{ A \subset E \; }[/math] и различных [math]\displaystyle{ x, y \in E - A \; }[/math]. Рассмотрим два подмножества A, B множества E. Если [math]\displaystyle{ A \subseteq B \; }[/math] или [math]\displaystyle{ B \subseteq A \; }[/math], тогда тривиально получается
[math]\displaystyle{ f(A) + f(B) \ge f(A \cup B) + f(A \cap B) \; }[/math].
Следовательно, должно иметь место [math]\displaystyle{ A \backslash B \ne \empty \; }[/math] и [math]\displaystyle{ B \backslash A \ne \empty \; }[/math]. Запишем это как [math]\displaystyle{ A \backslash B = \{ x_1, ..., x_k \} \; }[/math] и [math]\displaystyle{ B \backslash A = \{ y_1, ..., y_h \} \; }[/math]. Тогда
[math]\displaystyle{ f(A \; \cup \; B) - f(A) - f(B) + f(A \; \cap \; B) = \sum^k_{i = 1} \sum^h_{j = 1} \Delta_{x_i} \Delta_{y_j} f(A \; \cup \; \{ x_1, ..., x_{i - 1} \} \; \cup \; \{ y_1, ..., y_{j - 1} \}) \le 0 }[/math],
где [math]\displaystyle{ \{ x_1, ..., x_{i - 1} \} = \empty \; }[/math] для i = 1 и [math]\displaystyle{ \{ y_1, ..., y_{j - 1} \} = \empty \; }[/math] для j = 1.
Лемма 2. Определим f(H) = -mst(P : H). Тогда функция f является субмодулярной над множеством ребер E.
Доказательство. Заметим, что для любых двух различных ребер x и y, не принадлежащих подграфу H,
[math]\displaystyle{ \Delta_x \Delta_y f(H) = -mst(P : H \; \cup \; x \; \cup \; y) + mst(P : H \; \cup \; x) + mst(P : H \; \cup \; y) - mst(P : H) = (mst(P : H) - mst(P : H \; \cup x \; \cup \; y)) - (mst(P : H) - mst(P : H \; \cup \; x)) + (mst(P : H) - mst(P : H \; \cup \; y)) }[/math].
Пусть T – минимальное остовное дерево для несвязанных полюсов после стягивания каждого ребра H в точку. T содержит путь [math]\displaystyle{ P_x \; }[/math], соединяющий две конечные точки x, и путь [math]\displaystyle{ P_y \; }[/math], соединяющий две конечные точки y. Пусть [math]\displaystyle{ e_x (e_y) \; }[/math] – самое длинное ребро пути [math]\displaystyle{ P_x (P_y) \; }[/math]. Тогда
[math]\displaystyle{ mst(P : H) - mst(P : H \; \cup \; x) = length(e_x) }[/math];
[math]\displaystyle{ mst(P : H) - mst(P : H \; \cup \; y) = length(e_y) }[/math].
Значение [math]\displaystyle{ mst(P : H) - mst(P : H \; \cup \; x \; \cup \; y) }[/math] можно вычислить следующим образом: выберем самое длинное ребро e' из [math]\displaystyle{ P_x \cup P_y }[/math]. Заметим, что [math]\displaystyle{ T \cup x \cup y - e' }[/math] содержит уникальный цикл Q. Выберем самое длинное ребро e" из [math]\displaystyle{ (P_x \cup P_y) \cap Q }[/math]. Тогда
[math]\displaystyle{ mst(P : H) - mst(P : H \cup x \cup y) = length(e') + length(e'') }[/math].
Теперь, чтобы показать субмодулярность f, достаточно доказать неравенство
(2) [math]\displaystyle{ length(e_x) + length(e_y) \ge length(e') + length(e'') }[/math].
Случай 1. [math]\displaystyle{ e_x \notin P_x \cap P_y }[/math] и [math]\displaystyle{ e_y \notin P_x \cap P_y }[/math]. Без потери общности будем считать, что [math]\displaystyle{ length(e_x) \ge length(e_y) \; }[/math]. Тогда можно выбрать [math]\displaystyle{ e' = e_x \; }[/math] таким образом, что [math]\displaystyle{ (P_x \cup P_y) \cap Q = P_y }[/math]. Следовательно, можно выбрать [math]\displaystyle{ e'' = e_y \; }[/math]. Таким образом, выполняется равенство для (2).
Случай 2. [math]\displaystyle{ e_x \notin P_x \cap P_y }[/math] и [math]\displaystyle{ e_y \in P_x \cap P_y }[/math]. Очевидно, что [math]\displaystyle{ length(e_x) \ge length(e_y) }[/math]. Тогда можно выбрать [math]\displaystyle{ e' = e_x \; }[/math] таким образом, что [math]\displaystyle{ (P_x \cup P_y) \cap Q = P_y }[/math]. Следовательно, можно выбрать [math]\displaystyle{ e'' = e_y \; }[/math]. Таким образом, выполняется равенство для (2).
Случай 3. [math]\displaystyle{ e_x \in P_x \cap P_y }[/math] и [math]\displaystyle{ e_y \notin P_x \cap P_y }[/math]. Аналогично случаю 2.
Случай 4. [math]\displaystyle{ e_x \in P_x \cap P_y }[/math] и [math]\displaystyle{ e_y \in P_x \cap P_y }[/math]. В этом случае [math]\displaystyle{ length(e_x) = length(e_y) = length(e') \; }[/math]. Таким образом, (2) верно. □
Далее поясняется, что субмодулярность gain([math]\displaystyle{ \cdot }[/math]) имеет место для k-ограниченного дерева Штейнера.
Предположение. Пусть [math]\displaystyle{ \mathcal{E} \; }[/math] – множество всех полных компонентов дерева Штейнера. Тогда gain([math]\displaystyle{ \cdot }[/math]) как функция от множества всех подмножеств [math]\displaystyle{ \mathcal{E} \; }[/math] является субмодулярной.
Доказательство. Заметим, что для любых [math]\displaystyle{ \mathcal{H} \subset \mathcal{E} \; }[/math] и [math]\displaystyle{ x, y \in \mathcal{E} - \mathcal{H} \; }[/math] верно [math]\displaystyle{ \Delta_x \Delta_y mst(H) = 0 \; }[/math], где [math]\displaystyle{ H = \cup_{z \in \mathcal{H}} z \; }[/math]. Таким образом, верность предположения следует из леммы 2. □
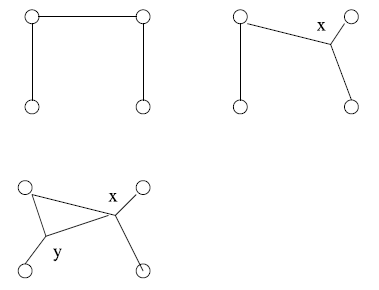
Пусть [math]\displaystyle{ \mathcal{F} \; }[/math] – множество трехлучевых звезд и ребер, выбранных жадным алгоритмом для вычисления итеративного 1-дерева Штейнера. Тогда gain([math]\displaystyle{ \cdot }[/math]) может и не быть субмодулярной на [math]\displaystyle{ \mathcal{F} \; }[/math]. Чтобы убедиться в этом, рассмотрим две трехлучевых звезды x и y на рис. 2. Заметим, что [math]\displaystyle{ gain(x \cup y) \gt gain(x), gain(y) \le 0, gain(\empty) = 0 \; }[/math]. Имеет место соотношение
[math]\displaystyle{ gain(x \cup y) - gain(x) - gain(y) + gain(\empty) \gt 0 \; }[/math].
Рисунок 2.
Применение
Задача построения дерева Штейнера является классической NP-полной проблемой и имеет множество приложений при разработке компьютерных микросхем, междугородних телефонных линий, многоадресной маршрутизации в сетях телекоммуникаций и т.п. Разработано множество эвристик жадного типа для построения деревьев Штейнера. Большинство из них демонстрируют высокую эффективность в компьютерных экспериментах, однако без подкрепления со стороны теоретического анализа. Предложенный подход может стать его основой.
Открытые вопросы
До сих пор неясно, является ли задача построения 3-ограниченного минимального дерева Штейнера NP-полной. Известно, что она является таковой при построении k-ограниченного минимального дерева Штейнера при [math]\displaystyle{ k \ge 4 \; }[/math].
См. также
Литература
1. Arora, S.: Polynomial-time approximation schemes for Euclidean TSP and other geometric problems. Proc. 37th IEEE Symp. on Foundations of Computer Science, pp. 2-12 (1996)
2. Berman, P., Ramaiyer, V.: Improved approximations for the Steiner tree problem. J. Algorithms 17, 381^08(1994)
3. Bern, M., Plassmann, P.: The Steiner problem with edge lengths 1 and 2. Inf. Proc. Lett. 32,171 -176 (1989)
4. Chang, S.K.: The generation of minimal trees with a Steiner topology. J.ACM 19,699-711 (1972)
5. Chang, S.K.: The design of network configurations with linear or piecewise linear cost functions. In: Symp. on Computer-Communications, Networks, and Teletraffic, pp. 363-369 IEEE Computer Society Press, California (1972)
6. Crourant, R., Robbins, H.: What Is Mathematics? Oxford University Press, New York (1941)
7. Du, D.Z., Hwang, F.K.: The Steiner ratio conjecture of Gilbert-Pollak is true. Proc. Natl. Acad. Sci. USA 87,9464-9466 (1990)
8. Du, D.Z., Zhang, Y., Feng, Q.: On better heuristic for euclidean Steiner minimum trees. In: Proceedings 32nd FOCS, IEEE Computer Society Press, California (1991)
9. Du, D.Z., Graham, R.L., Pardalos, P.M., Wan, P.J., Wu, W., Zhao, W.: Analysis of greedy approximations with nonsubmodular potential functions. In: Proceedings of 19th ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 167-175. ACM, New York (2008)
10. Kahng, A., Robins, G.: A new family of Steiner tree heuristics with good performance: the iterated 1-Steiner approach. In: Proceedings of IEEE Int. Conf. on Computer-Aided Design, Santa Clara, pp.428-431 (1990)
11. Wolsey, L.A.: An analysis of the greedy algorithm for the submodular set covering problem. Combinatorica 2, 385-393 (1982)
12. Robin, G., Zelikovsky, A.: Improved Steiner trees approximation in graphs. In: SIAM-ACM Symposium on Discrete Algorithms (SODA), San Francisco, CA, pp. 770-779. January (2000)
13. Smith, J.M., Lee, D.T., Liebman, J.S.: An O(N log N) heuristic for Steiner minimal tree problems in the Euclidean metric. Networks 11, 23-39 (1981)
14. Zelikovsky, A.Z.: The 11/6-approximation algorithm for the Steiner problem on networks. Algorithmica 9,463^70 (1993)