Прямолинейное остовное дерево: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 35 промежуточных версий 1 участника) | |||
| Строка 4: | Строка 4: | ||
== Постановка задачи == | == Постановка задачи == | ||
Пусть дано множество из n точек на плоскости. Остовное дерево представляет собой множество ребер, соединяющее все точки и не содержащее циклов. Если каждому ребру приписан вес при помощи некоторой метрики, связанной с расстоянием между инцидентными точками, то метрическим минимальным остовным деревом будет [[минимальное остовное дерево]] (МОД) с минимальной суммой этих весов. Если используется евклидово расстояние | Пусть дано множество из n точек на плоскости. [[Остовное дерево]] представляет собой множество ребер, соединяющее все точки и не содержащее циклов. Если каждому ребру приписан вес при помощи некоторой метрики, связанной с расстоянием между инцидентными точками, то ''метрическим минимальным остовным деревом'' будет [[минимальное остовное дерево]] (МОД) с минимальной суммой этих весов. Если используется евклидово расстояние <math>(L_2) \;</math>, такое дерево называется ''евклидовым МОД''; если расстояние по прямой <math>(L_1) \;</math>, то мы имеем дело с ''прямолинейным МОД''. | ||
Минимальные остовные деревья на взвешенных графах хорошо изучены. Обычный подход к построению метрического МОД заключается в определении [[взвешенный граф|взвешенного графа]] на множестве точек и затем в построении на его основе остовного дерева. | |||
Минимальные остовные деревья на взвешенных графах хорошо изучены. Обычный подход к построению метрического МОД заключается в определении [[взвешенный граф|взвешенного графа]] на множестве точек и затем в построении остовного дерева | |||
| Строка 16: | Строка 15: | ||
Поскольку остовные графы с меньшим числом ребер обеспечивают более эффективное построение минимального остовного дерева, мощность остовного графа определяется как количество ребер в нем. Легко увидеть, что полный граф на множестве точек содержит все остовные деревья и, в силу этого, является остовным графом. Однако мощность подобного графа составляет <math>O(n^2) \;</math>. Прямолинейный остовный граф мощности O(n) может быть построен за время O(n log n) [6]. | Поскольку остовные графы с меньшим числом ребер обеспечивают более эффективное построение минимального остовного дерева, [[мощность]] остовного графа определяется как количество ребер в нем. Легко увидеть, что полный граф на множестве точек содержит все остовные деревья и, в силу этого, является остовным графом. Однако мощность подобного графа составляет <math>O(n^2) \;</math>. Прямолинейный остовный граф мощности O(n) может быть построен за время O(n log n) [6]. | ||
Алгоритмы построения МОД обычно используют два свойства, позволяющие включать ребра в минимальное остовное дерево и исключать их. Первое свойство, известное как [[свойство разрезов]], гласит, что ребро с минимальным весом, | Алгоритмы построения МОД обычно используют два свойства, позволяющие включать ребра в минимальное остовное дерево и исключать их. Первое свойство, известное как [[свойство разрезов]], гласит, что ребро с минимальным весом, рассекающее любое разбиение множества вершин на два подмножества, принадлежит к МОД. Второе свойство называется [[свойство циклов|свойством циклов]] и утверждает, что ребро любого цикла графа, имеющее наибольший вес, можно безопасно удалить. Поскольку эти два свойства сформулированы в контексте построения минимального остовного дерева, они оказываются полезными для остовного графа. | ||
== Основные результаты == | == Основные результаты == | ||
| Строка 25: | Строка 24: | ||
'''Определение 2'''. Пусть имеется точка s; область R обладает свойством единственности относительно s, если для каждой пары точек <math>p, q \in R \;</math>, ||pq|| < max(||sp||, ||sq||). Разбиение пространства на | '''Определение 2'''. Пусть имеется точка s; область R обладает свойством единственности относительно s, если для каждой пары точек <math>p, q \in R \;</math>, ||pq|| < max(||sp||, ||sq||). Разбиение пространства на конечное множество непересекающихся областей обладает свойством единственности относительно s, если каждая из этих областей обладает свойством единственности относительно s. | ||
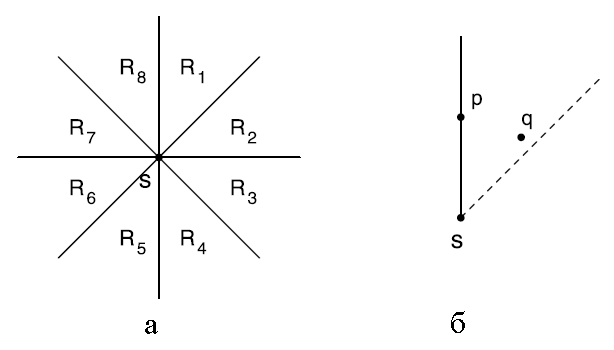
Нотация ||sp|| используется для представления расстояния между s и p согласно метрике | Нотация ||sp|| используется для представления расстояния между s и p согласно метрике <math>L_1 \;</math>. Определим ''восьмиугольное разбиение'' плоскости относительно точки s как разбиение, порожденное двумя прямыми линиями под углом 90 градусов и двумя прямыми под углом 45 градусов к ним, как показано на рис. 1(а). Здесь каждая из областей, от <math>R_1 \;</math> до <math>R_8 \;</math>, включает только одну из ограничивающих ее полупрямых, как можно видеть на рис. 1(б). Можно показать, что восьмиугольное разбиение обладает свойством единственности. | ||
| Строка 36: | Строка 35: | ||
Доказательство. Чтобы показать, что разбиение обладает свойством единственности, необходимо доказать, что каждая область разбиения обладает этим свойством. Поскольку области <math>R_1 - R_8 \;</math> аналогичны друг другу, достаточно будет доказать это для области <math>R_1 \;</math>. | Доказательство. Чтобы показать, что разбиение обладает свойством единственности, необходимо доказать, что каждая область разбиения обладает этим свойством. Поскольку области <math>R_1 - R_8 \;</math> аналогичны друг другу, достаточно будет доказать это для области <math>R_1 \;</math>. | ||
Точки в области <math>R_1 \;</math> можно охарактеризовать следующими неравенствами: <math>x \ge x_s; \; x - y < x_s - y_s</math>. | |||
Предположим, что имеются точки p и q в <math>R_1 \;</math>. Без потери общности будем считать, что <math>x_p \le x_q \;</math>. Если <math>y_p \le y_q \;</math>, то ||sq|| = ||sp|| + ||pq|| > ||pq||. Следовательно, необходимо рассмотреть только случай <math>y_p > y_q \;</math>. В этом случае <math>||pq|| = |x_p - x_q| + |y_p - y_q| = x_q - x_p + y_p - y_q = (x_q - y_q) + y_p - x_p < (x_s - y_s) + y_p - x_s = y_p - y_s \le x_p - x_s + y_p - y_s = ||sp||</math>. | |||
□ | |||
<math> | |||
[[Файл:RST_1.png]] | |||
Рис. 1. Восьмиугольное разбиение и свойство единственности. | |||
Рис. 1. | |||
Восьмиугольное разбиение и свойство единственности | |||
Пусть даны две точки p, q в одном и том же сегменте (октанте) восьмиугольного разбиения плоскости относительно точки s. Согласно свойству единственности, ||pq|| < max(||sp||; ||sq||). Рассмотрим цикл с точками s, p и q. Согласно свойству циклов, только одну точку с минимальным расстоянием до s необходимо соединить с s. Интересное свойство восьмиугольного разбиения заключается в том, что контур равноудаленных от s точек формирует отрезок прямой в каждой области. В областях <math>R_1, R_2, R_5, R_6 \;</math> эти сегменты описываются уравнением вида x + y = c; в областях <math>R_3, R_4, R_7, R_8 \;</math> – уравнением вида x - y = c. | Пусть даны две точки p, q в одном и том же сегменте (октанте) восьмиугольного разбиения плоскости относительно точки s. Согласно свойству единственности, ||pq|| < max(||sp||; ||sq||). Рассмотрим цикл с точками s, p и q. Согласно свойству циклов, только одну точку с минимальным расстоянием до s необходимо соединить с s. Интересное свойство восьмиугольного разбиения заключается в том, что контур равноудаленных от s точек формирует отрезок прямой в каждой области. В областях <math>R_1, R_2, R_5, R_6 \;</math> эти сегменты описываются уравнением вида x + y = c; в областях <math>R_3, R_4, R_7, R_8 \;</math> – уравнением вида x - y = c. | ||
Для каждой точки s необходимо найти ближайшего к ней соседа в каждом октанте. Опишем, как эффективно вычислить соседей в октанте <math>R_1 \;</math> для всех точек. Случаи остальных октантов симметричны. Для октанта <math>R_1 \;</math> алгоритм с заметающей прямой выполняется для всех точек в порядке неубывания x + y. В процессе заметания поддерживается [[активное множество]], состоящее из точек, для которых ближайшие соседи в <math>R_1 \;</math> еще не найдены. После обработки точки p будут найдены все точки активного множества, содержащие p в их областях <math>R_1 \;</math>. Если такая точка содержится в активном множестве, то, поскольку точки проверяются в порядке неубывания x + y, p должна быть ближайшей точкой для s в <math>R_1 \;</math>. Таким образом, будет добавлено ребро sp и точка s будет удалена из активного множества. После обработки этих активных точек точка p будет добавлена в активное множество. Каждая точка будет добавлена в активное множество и удалена из него только один раз. | |||
Для каждой точки s необходимо найти ближайшего к ней соседа в каждом октанте. Опишем, как эффективно вычислить соседей в октанте <math>R_1 \;</math> для всех точек. Случаи остальных октантов симметричны. Для октанта <math>R_1 \;</math> алгоритм с заметающей прямой | |||
Таким образом, будет добавлено ребро sp и точка s будет удалена из активного множества. После обработки этих активных точек точка p будет добавлена в активное множество. Каждая точка будет добавлена в активное множество и удалена из него только один раз. | |||
Фундаментальной операцией алгоритма с заметающей прямой является нахождение подмножества активных точек, такого, что заданная точка p принадлежит к их областям <math>R_1 \;</math>. Основываясь на наблюдении, что точка p принадлежит к области <math>R_1 \;</math> точки s в том и только том случае, если s принадлежит к области <math>R_5 \;</math> точки p, необходимо найти подмножество активных точек в области <math>R_5 \;</math> точки p. Поскольку область <math>R_5 \;</math> может быть представлена как двумерный диапазон ( | Фундаментальной операцией алгоритма с заметающей прямой является нахождение подмножества активных точек, такого, что заданная точка p принадлежит к их областям <math>R_1 \;</math>. Основываясь на наблюдении, что точка p принадлежит к области <math>R_1 \;</math> точки s в том и только том случае, если s принадлежит к области <math>R_5 \;</math> точки p, необходимо найти подмножество активных точек в области <math>R_5 \;</math> точки p. Поскольку область <math>R_5 \;</math> может быть представлена как двумерный диапазон <math>( - \infty ,x_p ] \times (x_p - y_p, + \infty) \;</math> на <math>(x, x - y) \;</math>, для поддержки множества активных точек можно использовать дерево поиска с приоритетами [1]. В силу того, что каждая операция вставки и удаления требует O(log n) времени, а операция запроса – O(log n+ k) времени, где k – количество объектов в диапазоне, общее время работы алгоритма с заметающей прямой составит O(n log n). Другие области могут быть обработаны аналогично <math>R_1 \;</math>, так что полное время работы алгоритма составит O(n log n). Дерево поиска с приоритетами – это структура данных, поддерживающая сбалансированность ради быстрого осуществления поиска. Она отлично работает для статических входных множеств. Если входное множество оказывается динамическим, перебалансировка дерева может представлять серьезную проблему. К счастью, активное множество имеет структуру, которая допускает альтернативное представление. Поскольку точка удаляется из активного множества, если найдена точка в ее области <math>R_1 \;</math>, никакая точка активного множества не может принадлежать к области <math>R_1 \;</math> другой точки множества. | ||
Лемма 2. Для любых двух точек p, q в | '''Лемма 2. Для любых двух точек p, q, входящих в активное множество, должно выполняться <math>x_p \ne x_q \;</math>, и если <math>x_p < x_q \;</math>, то <math>x_p - y_p \le x_q - y_q \;</math>.''' | ||
Основываясь на этом свойстве, можно упорядочить активное множество в соответствии с возрастанием x. Из этого следует неубывающий порядок x - y. Пусть дана точка s; точки, для которых s находится в их областях <math>R_1 \;</math>, должны удовлетворять следующим неравенствам: | Основываясь на этом свойстве, можно упорядочить активное множество в соответствии с возрастанием x. Из этого следует неубывающий порядок x - y. Пусть дана точка s; точки, для которых s находится в их областях <math>R_1 \;</math>, должны удовлетворять следующим неравенствам: <math>x \le x_s; \; x - y > x_s - y_s</math>. | ||
x | |||
Чтобы найти подмножество активных точек, для которых s находится в их областях <math>R_1 \;</math>, вначале необходимо найти наибольшее x, такое, что x < | Чтобы найти подмножество активных точек, для которых s находится в их областях <math>R_1 \;</math>, вначале необходимо найти наибольшее x, такое, что <math>x \le x_s \;</math>, а затем выполнять обработку в порядке убывания x, до тех пор, пока не будет достигнуто <math>x - y \ge x_s - y_s \;</math>. Поскольку упорядочение производится только по одному измерению, используя любое бинарное дерево поиска со стоимостью операций вставки, деления и запроса, равной O(log n), получаем алгоритм с временем выполнения O(n log n). Бинарные деревья поиска также требуют балансировки. Кроме того, можно использовать списки с пропусками [2], использующие рандомизацию во избежание проблемы явной балансировки, но демонстрирующие ожидаемое поведение на уровне O(log n). | ||
Внимательное рассмотрение также позволяет прийти к выводу, что после заметания области <math>R_1 \;</math> нет необходимости в заметании <math>R_5 \;</math>, поскольку все ребра, необходимые на данном этапе, уже | Внимательное рассмотрение также позволяет прийти к выводу, что после заметания области <math>R_1 \;</math> нет необходимости в заметании <math>R_5 \;</math>, поскольку все ребра, необходимые на данном этапе, уже включены или предполагаются. Более того, основываясь на информации из <math>R_5 \;</math>, количество реберных соединений можно еще больше сократить. Во время обработки заметающим процессом точки s он находит подмножество активных точек, содержащих s в их областях <math>R_1 \;</math>. Без потери общности будем считать, что к ним относятся точки p и q. Тогда p и q принадлежат к области <math>R_5 \;</math> точки s, что означает ||pq|| < max(||sp||; ||sq||). Следовательно, необходимо только соединить s с ближайшей активной точкой. | ||
| Строка 78: | Строка 69: | ||
for ( | '''for''' (i = 0; i < 2; i + +) { | ||
if ( | '''if''' (i == 0) отсортировать точки согласно порядку x + y; | ||
найти точки в А[1], А[2], такие, что p находится в их областях | '''else''' отсортировать точки согласно порядку x - y; | ||
соединить p с ближайшей точкой каждого подмножества; | A[l] = A[2] = <math>\empty</math> | ||
удалить подмножества из A[1], A[2], соответственно; | '''for''' каждой точки p по порядку { | ||
добавить p к A[1], A[2]; | найти точки в А[1], А[2], такие, что p находится в их областях <math>R_{2i+1}</math> и <math>R_{2i+2}</math>, соответственно; | ||
соединить p с ближайшей точкой каждого подмножества; | |||
удалить подмножества из A[1], A[2], соответственно; | |||
добавить p к A[1], A[2]; | |||
} | |||
} | |||
Рис. 2. | Рис. 2. Алгоритм вычисления прямолинейного остовного графа. | ||
Алгоритм вычисления прямолинейного остовного графа | |||
| Строка 92: | Строка 87: | ||
Теорема 3. Пусть имеется n точек на плоскости. Алгоритм вычисления прямолинейного остовного графа строит остовный граф за время O(n log n), при этом количество ребер графа составляет O(n). | '''Теорема 3. Пусть имеется n точек на плоскости. Алгоритм вычисления прямолинейного остовного графа строит остовный граф за время O(n log n), при этом количество ребер графа составляет O(n).''' | ||
Доказательство. Алгоритм может рассматриваться как механизм удаления ребер из полного графа. Как было отмечено выше, все удаленные ребра являются избыточными согласно правилу циклов. Таким образом, граф на выходе алгоритма будет содержать по меньшей мере одно прямолинейное минимальное остовное дерево. | Доказательство. Алгоритм может рассматриваться как механизм удаления ребер из полного графа. Как было отмечено выше, все удаленные ребра являются избыточными согласно правилу циклов. Таким образом, граф на выходе алгоритма будет содержать по меньшей мере одно прямолинейное минимальное остовное дерево. | ||
За время работы алгоритма каждая точка будет добавлена в активное множество и удалена из него только один раз для каждой из областей <math>R_1 - R_4 \;</math>. Каждая операция вставки и удаления требует O(log n) времени. Таким образом, верхняя граница временной сложности алгоритма оказывается равной O(n log n). Хранить необходимо только активные множества, так что объем памяти для хранения не превышает O(n). □ | |||
== Применение == | == Применение == | ||
Алгоритм построения прямолинейного минимального остовного дерева широко применяется в САПР для проектирования СБИС. Он часто используется в качестве метрики для оценки длины кабелей в процессе размещения. Прямолинейные МОД нередко вычисляются для аппроксимации дерева Штейнера и являются ключевым компонентом многих эвристик дерева Штейнера. Также они | Алгоритм построения прямолинейного минимального остовного дерева широко применяется в САПР для проектирования СБИС. Он часто используется в качестве метрики для оценки длины кабелей в процессе размещения. Прямолинейные МОД нередко вычисляются для аппроксимации дерева Штейнера и являются ключевым компонентом многих эвристик дерева Штейнера. Также они используются для аппроксимации задачи коммивояжера, которая может применяться для генерации цепей сканирования при тестировании. Важно подчеркнуть, что в реальных приложениях размеры входных объектов обычно очень велики. Поскольку эта задача будет вычисляться сотни тысяч раз и во многих случаях на очень больших входных значениях, для вычисления прямолинейного МОД нужен очень эффективный алгоритм. | ||
== Экспериментальные результаты == | |||
Экспериментальные результаты построения прямолинейного остовного графа (ПОГ) на основе алгоритма Крускала для вычисления прямолинейного МОД были представлены Чжоу и др. [5]. В сравнении участвовали два других подхода. Первый подход использовал полный граф на множестве точек в качестве входного для алгоритма Крускала. Второй подход представлял собой реализацию концепции, предложенной в [3]: для каждой точки просканировать все остальные точки, но соединить ее только с ближайшей точкой в каждом квадранте. В эксперименте использовались множества от 1000 до 20000 точек, сгенерированные случайным образом. Результаты эксперимента представлены в таблице 1. В первом столбце указано количество сгенерированных точек; во втором – количество различающихся точек. Для каждого подхода приведены количество ребер в заданном графе и общее время выполнения. Если количество точек на входе было больше 10000, подходу на основе полного графа попросту не хватало памяти. | |||
{| | {| class = "wikitable" | ||
! style="background:#efefef;" colspan="2" width="200" | Вход | ! style="background:#efefef;" colspan="2" width="200" | Вход | ||
! style="background:#efefef;" colspan="2" | Полный | ! style="background:#efefef;" colspan="2" | Полный | ||
! style="background:#efefef;" colspan="2" | | ! style="background:#efefef;" colspan="2" | С огр. степени | ||
! style="background:#efefef;" colspan="2" | | ! style="background:#efefef;" colspan="2" | ПОГ | ||
|- | |- | ||
! style="background:#efefef;" | исх. | ! style="background:#efefef;" | исх. | ||
! style="background:#efefef;" | разл. | ! style="background:#efefef;" | разл. | ||
! style="background:#efefef;" | | ! style="background:#efefef;" | кол-во ребер | ||
! style="background:#efefef;" | время | ! style="background:#efefef;" | время | ||
! style="background:#efefef;" | | ! style="background:#efefef;" | кол-во ребер | ||
! style="background:#efefef;" | время | ! style="background:#efefef;" | время | ||
! style="background:#efefef;" | | ! style="background:#efefef;" | кол-во ребер | ||
! style="background:#efefef;" | время | ! style="background:#efefef;" | время | ||
|- | |- | ||
| Строка 142: | Строка 139: | ||
|} | |} | ||
Таблица 1. Экспериментальные результаты | Таблица 1. Экспериментальные результаты. | ||
| Строка 164: | Строка 158: | ||
6. Zhou, H., Shenoy, N., Nicholls, W.: Efficient spanning tree construction without delaunay triangulation. Inf. Proc. Lett. 81, 271-276(2002) | 6. Zhou, H., Shenoy, N., Nicholls, W.: Efficient spanning tree construction without delaunay triangulation. Inf. Proc. Lett. 81, 271-276(2002) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 04:57, 22 ноября 2024
Ключевые слова и синонимы
Метрическое минимальное остовное дерево; прямолинейный остовный граф
Постановка задачи
Пусть дано множество из n точек на плоскости. Остовное дерево представляет собой множество ребер, соединяющее все точки и не содержащее циклов. Если каждому ребру приписан вес при помощи некоторой метрики, связанной с расстоянием между инцидентными точками, то метрическим минимальным остовным деревом будет минимальное остовное дерево (МОД) с минимальной суммой этих весов. Если используется евклидово расстояние [math]\displaystyle{ (L_2) \; }[/math], такое дерево называется евклидовым МОД; если расстояние по прямой [math]\displaystyle{ (L_1) \; }[/math], то мы имеем дело с прямолинейным МОД.
Минимальные остовные деревья на взвешенных графах хорошо изучены. Обычный подход к построению метрического МОД заключается в определении взвешенного графа на множестве точек и затем в построении на его основе остовного дерева.
Подобно тому, как для поиска по лабиринту строится граф связей [4], для построения минимального остовного дерева можно определить остовный граф.
Определение 1. Пусть дано множество точек V на плоскости. Неориентированный граф G = (V, E) называется остовным графом, если он содержит минимальное остовное дерево для точек V на плоскости.
Поскольку остовные графы с меньшим числом ребер обеспечивают более эффективное построение минимального остовного дерева, мощность остовного графа определяется как количество ребер в нем. Легко увидеть, что полный граф на множестве точек содержит все остовные деревья и, в силу этого, является остовным графом. Однако мощность подобного графа составляет [math]\displaystyle{ O(n^2) \; }[/math]. Прямолинейный остовный граф мощности O(n) может быть построен за время O(n log n) [6].
Алгоритмы построения МОД обычно используют два свойства, позволяющие включать ребра в минимальное остовное дерево и исключать их. Первое свойство, известное как свойство разрезов, гласит, что ребро с минимальным весом, рассекающее любое разбиение множества вершин на два подмножества, принадлежит к МОД. Второе свойство называется свойством циклов и утверждает, что ребро любого цикла графа, имеющее наибольший вес, можно безопасно удалить. Поскольку эти два свойства сформулированы в контексте построения минимального остовного дерева, они оказываются полезными для остовного графа.
Основные результаты
На базе терминологии, данной в работе [3], определим свойство единственности следующим образом.
Определение 2. Пусть имеется точка s; область R обладает свойством единственности относительно s, если для каждой пары точек [math]\displaystyle{ p, q \in R \; }[/math], ||pq|| < max(||sp||, ||sq||). Разбиение пространства на конечное множество непересекающихся областей обладает свойством единственности относительно s, если каждая из этих областей обладает свойством единственности относительно s.
Нотация ||sp|| используется для представления расстояния между s и p согласно метрике [math]\displaystyle{ L_1 \; }[/math]. Определим восьмиугольное разбиение плоскости относительно точки s как разбиение, порожденное двумя прямыми линиями под углом 90 градусов и двумя прямыми под углом 45 градусов к ним, как показано на рис. 1(а). Здесь каждая из областей, от [math]\displaystyle{ R_1 \; }[/math] до [math]\displaystyle{ R_8 \; }[/math], включает только одну из ограничивающих ее полупрямых, как можно видеть на рис. 1(б). Можно показать, что восьмиугольное разбиение обладает свойством единственности.
Лемма 1. Пусть имеется точка s на плоскости. Восьмиугольное разбиение относительно s обладает свойством единственности.
Доказательство. Чтобы показать, что разбиение обладает свойством единственности, необходимо доказать, что каждая область разбиения обладает этим свойством. Поскольку области [math]\displaystyle{ R_1 - R_8 \; }[/math] аналогичны друг другу, достаточно будет доказать это для области [math]\displaystyle{ R_1 \; }[/math].
Точки в области [math]\displaystyle{ R_1 \; }[/math] можно охарактеризовать следующими неравенствами: [math]\displaystyle{ x \ge x_s; \; x - y \lt x_s - y_s }[/math].
Предположим, что имеются точки p и q в [math]\displaystyle{ R_1 \; }[/math]. Без потери общности будем считать, что [math]\displaystyle{ x_p \le x_q \; }[/math]. Если [math]\displaystyle{ y_p \le y_q \; }[/math], то ||sq|| = ||sp|| + ||pq|| > ||pq||. Следовательно, необходимо рассмотреть только случай [math]\displaystyle{ y_p \gt y_q \; }[/math]. В этом случае [math]\displaystyle{ ||pq|| = |x_p - x_q| + |y_p - y_q| = x_q - x_p + y_p - y_q = (x_q - y_q) + y_p - x_p \lt (x_s - y_s) + y_p - x_s = y_p - y_s \le x_p - x_s + y_p - y_s = ||sp|| }[/math]. □
Рис. 1. Восьмиугольное разбиение и свойство единственности.
Пусть даны две точки p, q в одном и том же сегменте (октанте) восьмиугольного разбиения плоскости относительно точки s. Согласно свойству единственности, ||pq|| < max(||sp||; ||sq||). Рассмотрим цикл с точками s, p и q. Согласно свойству циклов, только одну точку с минимальным расстоянием до s необходимо соединить с s. Интересное свойство восьмиугольного разбиения заключается в том, что контур равноудаленных от s точек формирует отрезок прямой в каждой области. В областях [math]\displaystyle{ R_1, R_2, R_5, R_6 \; }[/math] эти сегменты описываются уравнением вида x + y = c; в областях [math]\displaystyle{ R_3, R_4, R_7, R_8 \; }[/math] – уравнением вида x - y = c.
Для каждой точки s необходимо найти ближайшего к ней соседа в каждом октанте. Опишем, как эффективно вычислить соседей в октанте [math]\displaystyle{ R_1 \; }[/math] для всех точек. Случаи остальных октантов симметричны. Для октанта [math]\displaystyle{ R_1 \; }[/math] алгоритм с заметающей прямой выполняется для всех точек в порядке неубывания x + y. В процессе заметания поддерживается активное множество, состоящее из точек, для которых ближайшие соседи в [math]\displaystyle{ R_1 \; }[/math] еще не найдены. После обработки точки p будут найдены все точки активного множества, содержащие p в их областях [math]\displaystyle{ R_1 \; }[/math]. Если такая точка содержится в активном множестве, то, поскольку точки проверяются в порядке неубывания x + y, p должна быть ближайшей точкой для s в [math]\displaystyle{ R_1 \; }[/math]. Таким образом, будет добавлено ребро sp и точка s будет удалена из активного множества. После обработки этих активных точек точка p будет добавлена в активное множество. Каждая точка будет добавлена в активное множество и удалена из него только один раз.
Фундаментальной операцией алгоритма с заметающей прямой является нахождение подмножества активных точек, такого, что заданная точка p принадлежит к их областям [math]\displaystyle{ R_1 \; }[/math]. Основываясь на наблюдении, что точка p принадлежит к области [math]\displaystyle{ R_1 \; }[/math] точки s в том и только том случае, если s принадлежит к области [math]\displaystyle{ R_5 \; }[/math] точки p, необходимо найти подмножество активных точек в области [math]\displaystyle{ R_5 \; }[/math] точки p. Поскольку область [math]\displaystyle{ R_5 \; }[/math] может быть представлена как двумерный диапазон [math]\displaystyle{ ( - \infty ,x_p ] \times (x_p - y_p, + \infty) \; }[/math] на [math]\displaystyle{ (x, x - y) \; }[/math], для поддержки множества активных точек можно использовать дерево поиска с приоритетами [1]. В силу того, что каждая операция вставки и удаления требует O(log n) времени, а операция запроса – O(log n+ k) времени, где k – количество объектов в диапазоне, общее время работы алгоритма с заметающей прямой составит O(n log n). Другие области могут быть обработаны аналогично [math]\displaystyle{ R_1 \; }[/math], так что полное время работы алгоритма составит O(n log n). Дерево поиска с приоритетами – это структура данных, поддерживающая сбалансированность ради быстрого осуществления поиска. Она отлично работает для статических входных множеств. Если входное множество оказывается динамическим, перебалансировка дерева может представлять серьезную проблему. К счастью, активное множество имеет структуру, которая допускает альтернативное представление. Поскольку точка удаляется из активного множества, если найдена точка в ее области [math]\displaystyle{ R_1 \; }[/math], никакая точка активного множества не может принадлежать к области [math]\displaystyle{ R_1 \; }[/math] другой точки множества.
Лемма 2. Для любых двух точек p, q, входящих в активное множество, должно выполняться [math]\displaystyle{ x_p \ne x_q \; }[/math], и если [math]\displaystyle{ x_p \lt x_q \; }[/math], то [math]\displaystyle{ x_p - y_p \le x_q - y_q \; }[/math].
Основываясь на этом свойстве, можно упорядочить активное множество в соответствии с возрастанием x. Из этого следует неубывающий порядок x - y. Пусть дана точка s; точки, для которых s находится в их областях [math]\displaystyle{ R_1 \; }[/math], должны удовлетворять следующим неравенствам: [math]\displaystyle{ x \le x_s; \; x - y \gt x_s - y_s }[/math].
Чтобы найти подмножество активных точек, для которых s находится в их областях [math]\displaystyle{ R_1 \; }[/math], вначале необходимо найти наибольшее x, такое, что [math]\displaystyle{ x \le x_s \; }[/math], а затем выполнять обработку в порядке убывания x, до тех пор, пока не будет достигнуто [math]\displaystyle{ x - y \ge x_s - y_s \; }[/math]. Поскольку упорядочение производится только по одному измерению, используя любое бинарное дерево поиска со стоимостью операций вставки, деления и запроса, равной O(log n), получаем алгоритм с временем выполнения O(n log n). Бинарные деревья поиска также требуют балансировки. Кроме того, можно использовать списки с пропусками [2], использующие рандомизацию во избежание проблемы явной балансировки, но демонстрирующие ожидаемое поведение на уровне O(log n).
Внимательное рассмотрение также позволяет прийти к выводу, что после заметания области [math]\displaystyle{ R_1 \; }[/math] нет необходимости в заметании [math]\displaystyle{ R_5 \; }[/math], поскольку все ребра, необходимые на данном этапе, уже включены или предполагаются. Более того, основываясь на информации из [math]\displaystyle{ R_5 \; }[/math], количество реберных соединений можно еще больше сократить. Во время обработки заметающим процессом точки s он находит подмножество активных точек, содержащих s в их областях [math]\displaystyle{ R_1 \; }[/math]. Без потери общности будем считать, что к ним относятся точки p и q. Тогда p и q принадлежат к области [math]\displaystyle{ R_5 \; }[/math] точки s, что означает ||pq|| < max(||sp||; ||sq||). Следовательно, необходимо только соединить s с ближайшей активной точкой.
[math]\displaystyle{ R_1 \; }[/math] и [math]\displaystyle{ R_2 \; }[/math] имеют одну и ту же последовательность заметания и в силу этого могут быть обработаны вместе за один проход алгоритма. Аналогично, области [math]\displaystyle{ R_3 \; }[/math] и [math]\displaystyle{ R_4 \; }[/math] могут быть обработаны вместе за второй проход. На основе вышеприведенных рассуждений составим псевдокод алгоритма, представленный на рис. 2.
for (i = 0; i < 2; i + +) {
if (i == 0) отсортировать точки согласно порядку x + y;
else отсортировать точки согласно порядку x - y;
A[l] = A[2] = [math]\displaystyle{ \empty }[/math]
for каждой точки p по порядку {
найти точки в А[1], А[2], такие, что p находится в их областях [math]\displaystyle{ R_{2i+1} }[/math] и [math]\displaystyle{ R_{2i+2} }[/math], соответственно;
соединить p с ближайшей точкой каждого подмножества;
удалить подмножества из A[1], A[2], соответственно;
добавить p к A[1], A[2];
}
}
Рис. 2. Алгоритм вычисления прямолинейного остовного графа.
Корректность этого алгоритма устанавливает следующая теорема.
Теорема 3. Пусть имеется n точек на плоскости. Алгоритм вычисления прямолинейного остовного графа строит остовный граф за время O(n log n), при этом количество ребер графа составляет O(n).
Доказательство. Алгоритм может рассматриваться как механизм удаления ребер из полного графа. Как было отмечено выше, все удаленные ребра являются избыточными согласно правилу циклов. Таким образом, граф на выходе алгоритма будет содержать по меньшей мере одно прямолинейное минимальное остовное дерево.
За время работы алгоритма каждая точка будет добавлена в активное множество и удалена из него только один раз для каждой из областей [math]\displaystyle{ R_1 - R_4 \; }[/math]. Каждая операция вставки и удаления требует O(log n) времени. Таким образом, верхняя граница временной сложности алгоритма оказывается равной O(n log n). Хранить необходимо только активные множества, так что объем памяти для хранения не превышает O(n). □
Применение
Алгоритм построения прямолинейного минимального остовного дерева широко применяется в САПР для проектирования СБИС. Он часто используется в качестве метрики для оценки длины кабелей в процессе размещения. Прямолинейные МОД нередко вычисляются для аппроксимации дерева Штейнера и являются ключевым компонентом многих эвристик дерева Штейнера. Также они используются для аппроксимации задачи коммивояжера, которая может применяться для генерации цепей сканирования при тестировании. Важно подчеркнуть, что в реальных приложениях размеры входных объектов обычно очень велики. Поскольку эта задача будет вычисляться сотни тысяч раз и во многих случаях на очень больших входных значениях, для вычисления прямолинейного МОД нужен очень эффективный алгоритм.
Экспериментальные результаты
Экспериментальные результаты построения прямолинейного остовного графа (ПОГ) на основе алгоритма Крускала для вычисления прямолинейного МОД были представлены Чжоу и др. [5]. В сравнении участвовали два других подхода. Первый подход использовал полный граф на множестве точек в качестве входного для алгоритма Крускала. Второй подход представлял собой реализацию концепции, предложенной в [3]: для каждой точки просканировать все остальные точки, но соединить ее только с ближайшей точкой в каждом квадранте. В эксперименте использовались множества от 1000 до 20000 точек, сгенерированные случайным образом. Результаты эксперимента представлены в таблице 1. В первом столбце указано количество сгенерированных точек; во втором – количество различающихся точек. Для каждого подхода приведены количество ребер в заданном графе и общее время выполнения. Если количество точек на входе было больше 10000, подходу на основе полного графа попросту не хватало памяти.
| Вход | Полный | С огр. степени | ПОГ | ||||
|---|---|---|---|---|---|---|---|
| исх. | разл. | кол-во ребер | время | кол-во ребер | время | кол-во ребер | время |
| 1000 | 999 | 498501 | 5,095 с | 3878 | 0,299 с | 2571 | 0,112 с |
| 2000 | 1996 | 1991010 | 24,096 с | 7825 | 0,996 с | 5158 | 0,218 с |
| 4000 | 3995 | 7978015 | 2 м 7,233 с | 15761 | 3,452 с | 10416 | 0,337 с |
| 6000 | 5991 | 17943045 | 5 м 54,697 с | 23704 | 7,515 с | 15730 | 0,503 с |
| 8000 | 7981 | 31844190 | 13 м 7,682 с | 31624 | 13,141 с | 21149 | 0,672 с |
| 10000 | 9962 | 49615741 | - | 39510 | 20,135 с | 26332 | 0,934 с |
| 12000 | 11948 | - | - | 47424 | 32,300 с | 31586 | 1,052 с |
| 14000 | 13914 | - | - | 55251 | 46,842 с | 36853 | 1,322 с |
| 16000 | 15883 | - | - | 63089 | 1 м 3,759 с | 42251 | 1,486 с |
| 18000 | 17837 | - | - | 70876 | 1 м 19,812 с | 47511 | 1,701 с |
| 20000 | 19805 | - | - | 78723 | 1 м 45,792 с | 52732 | 1,907 с |
Таблица 1. Экспериментальные результаты.
См. также
Литература
1. McCreight, E.M.: Priority search trees. SIAM J. Comput. 14, 257-276(1985)
2. Pugh, W.: Skip lists: A probabilistic alternative to balanced trees. Commun. ACM 33,668-676 (1990)
3. Robins, G., Salowe, J.S.: Low-degree minimum spanning tree. Discret. Comput. Geom. 14,151-165 (1995)
4. Zheng, S.Q., Lim, J.S., Iyengar, S.S.: Finding obstacle-avoiding shortest paths using implicit connection graphs. IEEE Trans. Comput. Aided Des. 15,103-110 (1996)
5. Zhou, H., Shenoy, N., Nicholls, W.: Efficient minimum spanning tree construction without delaunay triangulation. In: Proc. Asian and South Pacific Design Automation Conference, Yokohama, Japan (2001)
6. Zhou, H., Shenoy, N., Nicholls, W.: Efficient spanning tree construction without delaunay triangulation. Inf. Proc. Lett. 81, 271-276(2002)