Общий алгоритм обхода графа с запоминанием дуг: различия между версиями
KVN (обсуждение | вклад) |
KVN (обсуждение | вклад) (→Задача) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
== Задача == | == Задача == | ||
О б ъ е к т ы. Ориентированный граф <math>G</math>, каждая вершина которого может находиться в одном из двух состояний: "помечена", "непомечена". | О б ъ е к т ы. [[Ориентированный граф]] <math>G</math>, каждая [[вершина]] которого может находиться в одном из двух состояний: "помечена", "непомечена". | ||
О п е р а ц и и. Для любой вершины <math>p</math> графа <math>G</math> операция ПОМЕТИТЬ(<math>p</math>) выполнима, если <math>p</math> находится в состоянии "непомечена", и при своем выполнении переводит <math>p</math> в состояние "помечена", а предикат НЕПОМЕЧЕНА(<math>p</math>) ложен, если p находится в состоянии "помечена". | О п е р а ц и и. Для любой вершины <math>p</math> графа <math>G</math> операция ПОМЕТИТЬ(<math>p</math>) выполнима, если <math>p</math> находится в состоянии "непомечена", и при своем выполнении переводит <math>p</math> в состояние "помечена", а предикат НЕПОМЕЧЕНА(<math>p</math>) ложен, если p находится в состоянии "помечена". | ||
| Строка 16: | Строка 16: | ||
'''проц''' ЛЕС(<math>p_0</math>: ''вершина'') = | '''проц''' ЛЕС(<math>p_0</math>: ''вершина'') = | ||
::<math>S</math> : ''семейство дуг'' = <math>\empty</math>; | |||
::<math>q</math>: ''вершина'' = <math>p_0</math>; | |||
::<math>L</math> : '''начало''' ПОМЕТИТЬ(q); | |||
::::<math>S \Leftarrow \overline{\ni} </math>ИСХОД<math>\,(q)</math>; | |||
:::: '''пока''' <math>S \neq \empty </math> '''цикл''' | |||
::::::<math>q</math> := КОНЕЦ(<math>\overline{\ni}S</math>); | |||
::::::'''если''' НЕПОМЕЧЕНА(<math>q</math>) '''то начать''' <math>L</math> '''все''' | |||
:::: '''все''' | |||
:: '''конец''' | |||
'''все''' | '''все''' | ||
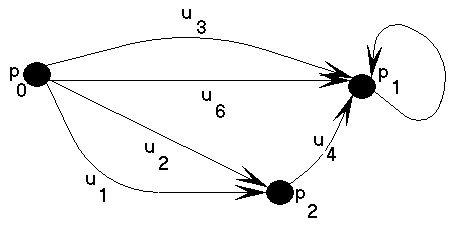
П о я с н е н и я. Рассмотрим граф | П о я с н е н и я. Рассмотрим следующий граф | ||
[[Файл:2-47.jpg]] | [[Файл:2-47.jpg]] | ||
При выполнении ЛЕС(<math>p_0</math>) состояние S меняется следующим образом: | При выполнении ЛЕС(<math>p_0</math>) состояние <math>S</math> меняется следующим образом: | ||
<math>\empty, \{ u_1,u_2,u_3 \}, \{ u_2,u_3 \}, \{ u_2,u_3,u_4 \}, \{u_3,u_4 \},\{ u_4 \}, \{ u_6,u_5,u_4 \}, \{ u_5,u_4 \}, \{ u_4\}, \empty</math> | <math>\empty, \{ u_1,u_2,u_3 \}, \{ u_2,u_3 \}, \{ u_2,u_3,u_4 \}, \{u_3,u_4 \},\{ u_4 \}, \{ u_6,u_5,u_4 \}, \{ u_5,u_4 \}, \{ u_4\}, \empty</math> | ||
Текущая версия от 04:57, 19 декабря 2011
Задача
О б ъ е к т ы. Ориентированный граф [math]\displaystyle{ G }[/math], каждая вершина которого может находиться в одном из двух состояний: "помечена", "непомечена".
О п е р а ц и и. Для любой вершины [math]\displaystyle{ p }[/math] графа [math]\displaystyle{ G }[/math] операция ПОМЕТИТЬ([math]\displaystyle{ p }[/math]) выполнима, если [math]\displaystyle{ p }[/math] находится в состоянии "непомечена", и при своем выполнении переводит [math]\displaystyle{ p }[/math] в состояние "помечена", а предикат НЕПОМЕЧЕНА([math]\displaystyle{ p }[/math]) ложен, если p находится в состоянии "помечена".
Д а н о. Задана вершина [math]\displaystyle{ p_0 }[/math] такая, что каждая вершина графа [math]\displaystyle{ G }[/math], достижимая из [math]\displaystyle{ p_0 }[/math], находится в состоянии "непомечена".
Т р е б у е т с я. Перевести в состояние "помечена" все вершины графа [math]\displaystyle{ G }[/math], достижимые из [math]\displaystyle{ p_0 }[/math].
З а м е ч а н и е. Предполагается, что процедура ПОМЕТИТЬ([math]\displaystyle{ p }[/math]) при своем выполнении осуществляет определенные действия с информационным содержимым вершины [math]\displaystyle{ p }[/math], для реализации которых и производится обход графа.
Решение
М е т о д.
проц ЛЕС([math]\displaystyle{ p_0 }[/math]: вершина) =
- [math]\displaystyle{ S }[/math] : семейство дуг = [math]\displaystyle{ \empty }[/math];
- [math]\displaystyle{ q }[/math]: вершина = [math]\displaystyle{ p_0 }[/math];
- [math]\displaystyle{ L }[/math] : начало ПОМЕТИТЬ(q);
- [math]\displaystyle{ S \Leftarrow \overline{\ni} }[/math]ИСХОД[math]\displaystyle{ \,(q) }[/math];
- пока [math]\displaystyle{ S \neq \empty }[/math] цикл
- [math]\displaystyle{ q }[/math] := КОНЕЦ([math]\displaystyle{ \overline{\ni}S }[/math]);
- если НЕПОМЕЧЕНА([math]\displaystyle{ q }[/math]) то начать [math]\displaystyle{ L }[/math] все
- все
- конец
все
П о я с н е н и я. Рассмотрим следующий граф
При выполнении ЛЕС([math]\displaystyle{ p_0 }[/math]) состояние [math]\displaystyle{ S }[/math] меняется следующим образом:
[math]\displaystyle{ \empty, \{ u_1,u_2,u_3 \}, \{ u_2,u_3 \}, \{ u_2,u_3,u_4 \}, \{u_3,u_4 \},\{ u_4 \}, \{ u_6,u_5,u_4 \}, \{ u_5,u_4 \}, \{ u_4\}, \empty }[/math]
а вершины графа посещаются в следующей последовательности:
[math]\displaystyle{ p_0, p_2, p_1 }[/math]
С в о й с т в а.
1. Временная сложность алгоритма составляет [math]\displaystyle{ O(k) }[/math] времени, где [math]\displaystyle{ k }[/math] — число дуг графа [math]\displaystyle{ G }[/math], достижимых из вершины [math]\displaystyle{ p_0 }[/math].
2. Алгоритм изменяет состояние непомеченной вершины [math]\displaystyle{ q }[/math] тогда и только тогда, когда [math]\displaystyle{ q }[/math] достижима из [math]\displaystyle{ p_0 }[/math].
3. Если [math]\displaystyle{ S }[/math] является стеком, то процедура помечает вершины графа [math]\displaystyle{ G }[/math], достижимые из [math]\displaystyle{ p_0 }[/math], в порядке поиска в глубину, а если [math]\displaystyle{ S }[/math] — очередь, то вершины помечаются в порядке поиска в ширину.
Литература
- Касьянов В. Н., Евстигнеев В. А. Графы в программировании: обработка, визуализация и применение. - СПб.: БХВ-Петербург, 2003, 1104 С.