Схемы Мартынюка: различия между версиями
Перейти к навигации
Перейти к поиску
KVN (обсуждение | вклад) (Отмена правки 5701 участника KVN (обсуждение)) |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
[[Файл:Martynyuk schemata.gif|200px|right]] | [[Файл:Martynyuk schemata.gif|200px|right]] | ||
'''Схемы Мартынюка''' (''[[Martynyuk schemata]]'') | '''Схемы Мартынюка''' (''[[Martynyuk schemata]]'') — | ||
подкласс ''неинтерпретированных схем'', | подкласс ''неинтерпретированных схем'', | ||
в которых не содержится | в которых не содержится | ||
| Строка 15: | Строка 15: | ||
здесь разрешима. | здесь разрешима. | ||
Схемы Мартынюка | Схемы Мартынюка — основная модель программы при решении | ||
задач анализа потока управления в программе. | задач анализа потока управления в программе. | ||
==См. также == | ==См. также == | ||
''[[Стандартные схемы]], [[Схема программ]], [[Схема с косвенной адресацией]], [[Схема с распределенной памятью]], [[Схемы Лаврова]], [[Схемы Янова]], [[Управляющий граф]].'' | * ''[[Стандартные схемы]],'' | ||
* ''[[Схема программ]],'' | |||
* ''[[Схема с косвенной адресацией]],'' | |||
* ''[[Схема с распределенной памятью]],'' | |||
* ''[[Схемы Лаврова]],'' | |||
* ''[[Схемы Янова]],'' | |||
* ''[[Управляющий граф]].'' | |||
==Литература== | ==Литература== | ||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
[[Категория:Теория схем программ]] | [[Категория:Теория схем программ]] | ||
Текущая версия от 04:43, 13 сентября 2011
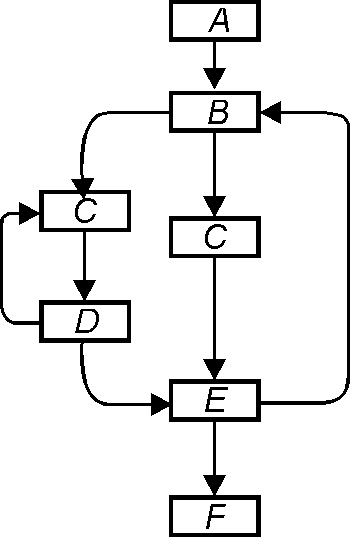
Схемы Мартынюка (Martynyuk schemata) — подкласс неинтерпретированных схем, в которых не содержится никакой информации о программе, кроме членения программы на операторы с указанием совпадающих (эквивалентно работающих) операторов и системы управляющих связей между операторами. Введены в литературу В.В.Мартынюком в 1961 г.
Как крупноблочная схема схема Мартынюка включает только одну переменную и состоит из операторов, каждый из которых имеет два операнда: обязательный вход и необязательный выход. Проблема распознавания эквивалентности здесь разрешима.
Схемы Мартынюка — основная модель программы при решении задач анализа потока управления в программе.
См. также
- Стандартные схемы,
- Схема программ,
- Схема с косвенной адресацией,
- Схема с распределенной памятью,
- Схемы Лаврова,
- Схемы Янова,
- Управляющий граф.
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.