Паросочетание: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Паросочетание''' (''Matching'') - произвольное подмножество попарно несмежных р...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Паросочетание''' (''Matching'') | '''Паросочетание''' (''[[Matching]]'') — | ||
произвольное подмножество попарно несмежных ребер графа. Паросочетание | произвольное подмножество попарно [[смежные ребра|несмежных ребер]] [[граф|графа]]. Паросочетание | ||
называется ''максимальным'', если оно не содержится в паросочетании с | называется ''максимальным'', если оно не содержится в паросочетании с | ||
большим числом ребер, и наибольшим, если число ребер в нем наибольшее | большим числом [[ребро|ребер]], и наибольшим, если число ребер в нем наибольшее | ||
среди всех паросочетаний графа. | среди всех паросочетаний графа. | ||
Другое название | Другое название — ''[[Независимое множество ребер графа|Независимое множество ребер]]''. | ||
См. также ''Вершинно-реберное инцидентное паросочетание, Правильное паросочетание, Совершенное паросочетание, Частичное паросочетание, Взаимные паросочетания.'' | [[Файл:Matching.png|200px]] | ||
==См. также== | |||
* ''[[Вершинно-реберное инцидентное паросочетание]],'' | |||
* ''[[Правильное паросочетание]],'' | |||
* ''[[Совершенное паросочетание]],'' | |||
* ''[[Частичное паросочетание]],'' | |||
* ''[[Взаимные паросочетания]].'' | |||
==Литература== | ==Литература== | ||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
Текущая версия от 04:41, 6 июня 2011
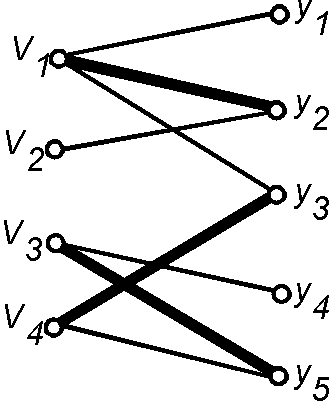
Паросочетание (Matching) — произвольное подмножество попарно несмежных ребер графа. Паросочетание называется максимальным, если оно не содержится в паросочетании с большим числом ребер, и наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа.
Другое название — Независимое множество ребер.
См. также
- Вершинно-реберное инцидентное паросочетание,
- Правильное паросочетание,
- Совершенное паросочетание,
- Частичное паросочетание,
- Взаимные паросочетания.
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.