Колесо: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Колесо''' (''Wheel'') - граф, определяемый как <math>W_{n} = K_{1} + C_{n-1}</math>, т.е. <math>n</math>-в...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
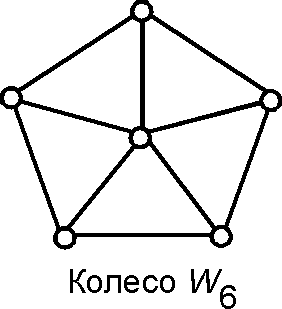
'''Колесо''' (''Wheel'') | '''Колесо''' (''[[Wheel]]'') — [[граф]], определяемый как <math>W_{n} = K_{1} + C_{n-1}</math>, т.е. <math>n</math>-[[вершина|вершинный]] граф, у которого <math>n-1</math> вершин принадлежат [[простой цикл|простому циклу]] <math>C_{n-1}</math> и одна вершина (вне этого [[цикл|цикла]]) [[смежные вершины|смежна]] со всеми остальными. Термин введен Таттом. | ||
граф, определяемый как <math>W_{n} = K_{1} + C_{n-1}</math>, т.е. <math>n</math>-вершинный | |||
граф, у которого <math>n-1</math> вершин принадлежат простому циклу <math>C_{n-1}</math> и | [[Файл:Wheel.png|200px]] | ||
одна вершина (вне этого цикла) смежна со всеми остальными. Термин | |||
введен Таттом. | |||
==Литература== | ==Литература== | ||
* Харари Ф. Теория графов. — М.: Мир, 1973. | |||
Текущая версия от 10:58, 28 марта 2011
Колесо (Wheel) — граф, определяемый как [math]\displaystyle{ W_{n} = K_{1} + C_{n-1} }[/math], т.е. [math]\displaystyle{ n }[/math]-вершинный граф, у которого [math]\displaystyle{ n-1 }[/math] вершин принадлежат простому циклу [math]\displaystyle{ C_{n-1} }[/math] и одна вершина (вне этого цикла) смежна со всеми остальными. Термин введен Таттом.
Литература
- Харари Ф. Теория графов. — М.: Мир, 1973.